Karthikdevan (Talk | contribs) |
|||
| (19 intermediate revisions by 2 users not shown) | |||
| Line 1: | Line 1: | ||
{{IIT-Madras-Top/CSS}} | {{IIT-Madras-Top/CSS}} | ||
| + | __TOC__ | ||
| + | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
= Modularity of RBS parts = | = Modularity of RBS parts = | ||
== Introduction == | == Introduction == | ||
| − | + | The '''non-modular nature''' of Ribosomal Binding Sites in bacteria is well known to the synthetic biology community. Most of the biological parts have been assigned a strength for their functionality. For example, Promoters have transcriptional score (number of RNA molecules per DNA molecule), RBSs have translational score (number of protein molecules per RNA molecule). Ideally, if we were to use a promoter and a RBS to produce a protein, we should get ('''transcriptional score times translational score''') number of protein molecules. In bacterial cells, transcription and translation processes are coupled and can occur simultaneously. This is why, these process are not independent and, hence, not modular. Apart from this, RNA molecules consisting of RBS and first few codons may form secondary structures, which in turn reduce the translation efficiency. Also, rare codons have also been shown to influence translation efficiency. | |
| − | + | ||
| − | + | Secondary structure's and codons' influence on translational score of RBS are overlapping as they are a result of '''A, U, G, C''' combinations. Therefore, it is important to decouple both effects to unravel underlying patterns. | |
| + | |||
| + | '''We have successfully validated an empirical model to predict variations in protein expression levels, which could help future iGEM teams'''. Here, we represent a thorough description of our work. | ||
== Methodology == | == Methodology == | ||
| − | + | The dataset from "Causes and effects of N-terminal codon bias in bacterial genes" paper was taken. Protein expression Data was available for following constructs : | |
| − | 2 promoters x 3 RBSs x 1781 (137x13) sfGFP variants in first 11 codons at N-terminal (3 RBS parts were B0034, B0032, B0030) and 2 promoter x 137 natural RBSs x 13 sfGFP variants in first 11 codons at N-terminal (2 Promoters were J23100 & J23108) | + | 2 promoters x 3 RBSs x 1781 (137x13) sfGFP variants in first 11 codons at N-terminal (3 RBS parts were B0034, B0032, B0030) and 2 promoter x 137 natural RBSs x 13 sfGFP variants in first 11 codons at N-terminal (2 Promoters were J23100 & J23108) |
== Hypothesis and Algorithm == | == Hypothesis and Algorithm == | ||
| − | + | At the beginning, we hypothesized following things based on the information available in literature:<br> | |
| − | Expression is inversely proportional to the stability of secondary structure of mRNA near RBS part. | + | 1. '''Expression is inversely proportional to the stability of secondary structure of mRNA near RBS part'''.<br> |
| − | Rare codons present in first 11 codons of proteins have the ability to increase or decrease the translational score of RBS parts. Each RBS part has a native strength irrespective of the promoter and protein coding part it can be used with. | + | 2. '''Rare codons present in first 11 codons of proteins have the ability to increase or decrease the translational score of RBS parts'''.<br> |
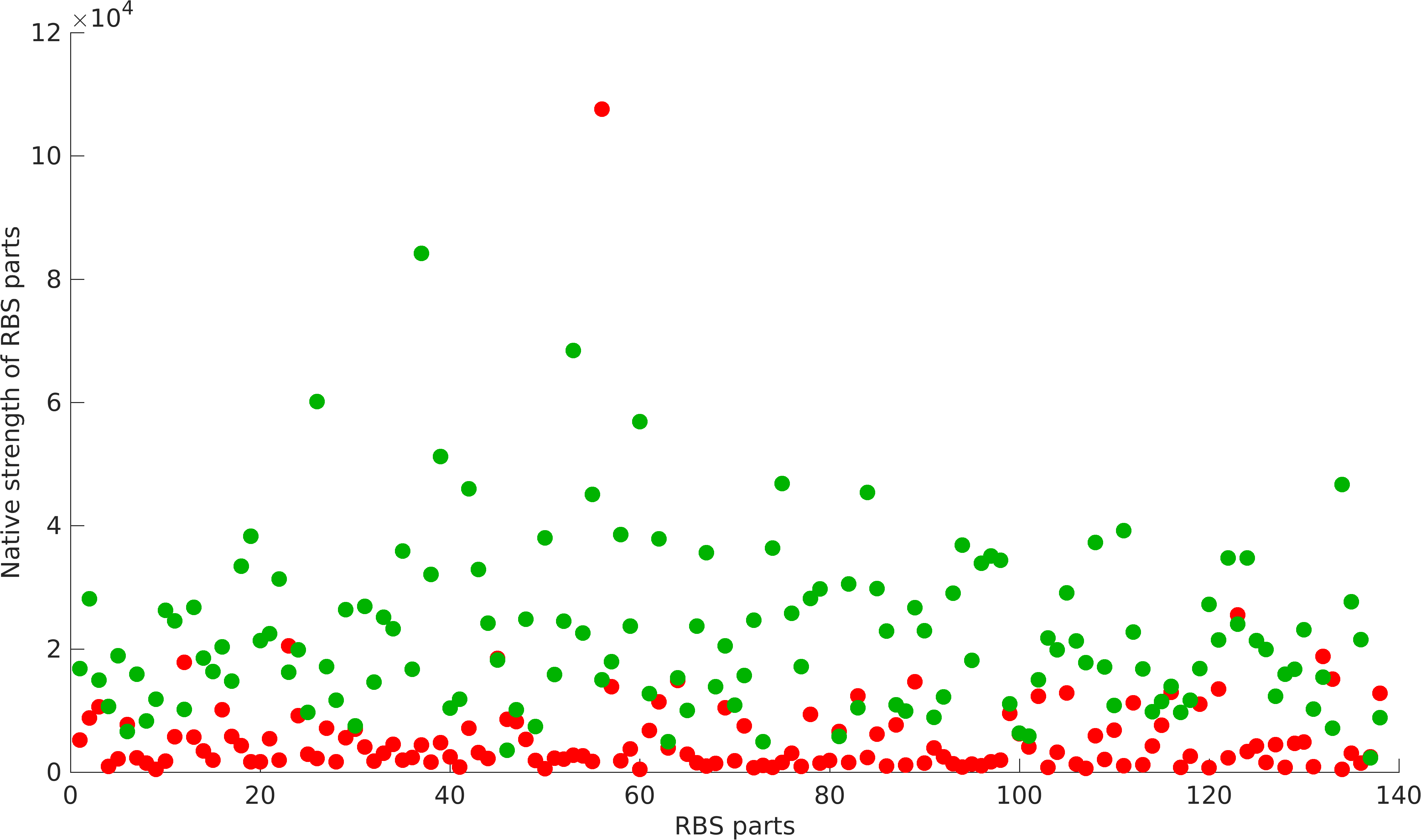
| + | 3. '''Each RBS part has a native strength irrespective of the promoter and protein coding part it can be used with'''. | ||
| − | + | We designed an algorithm to compute the translational score of a given construct(which expresses a protein) in the following way: | |
\begin{equation*} | \begin{equation*} | ||
TS = \dfrac{NS*C_{pref}}{1+dG} + \alpha | TS = \dfrac{NS*C_{pref}}{1+dG} + \alpha | ||
| Line 34: | Line 32: | ||
\end{equation*} | \end{equation*} | ||
| − | Objective | + | '''Objective Function''': minimize \(\sum \mid TS_{model}-TS_{experiment} \mid\) |
| − | Outlier Removal: top scores in \(\mid TS_{model}-TS_{experiment} \mid\) | + | '''Outlier Removal''': top scores in \(\mid TS_{model}-TS_{experiment} \mid\) |
where \(C_{i}\) is the codon preference of codon present at \(i^{th}\) position, \(C_{sfGFP}\) a constant for sfGFP protein codons, <br> | where \(C_{i}\) is the codon preference of codon present at \(i^{th}\) position, \(C_{sfGFP}\) a constant for sfGFP protein codons, <br> | ||
| − | TS : Translational Score of RBS part, <br> | + | '''TS''' : Translational Score of RBS part, <br> |
| − | NS : Native Strength of RBS part, which is equal to TS at \(\delta\)G=0, \(C_{pref}\)=1; <br> | + | '''NS''' : Native Strength of RBS part, which is equal to TS at \(\delta\)G=0, \(C_{pref}\)=1; <br> |
| − | \(\delta\)G : Stability of RNA strand consisting of RBS and first 11 codon of protein, <br> | + | '''\(\delta\)G''' : Stability of RNA strand consisting of RBS and first 11 codon of protein, <br> |
\(\alpha\) is a constant. | \(\alpha\) is a constant. | ||
== Quantification of Non-modularity == | == Quantification of Non-modularity == | ||
| − | + | As previously mentioned, RBS's have been found to be non-modular with respect to promoter and protein coding parts. A quantification of modularity would enable us to screen better RBS parts to make high order complex genetic circuits in high-throughput manner. | |
\begin{equation*} | \begin{equation*} | ||
| Line 51: | Line 49: | ||
NM_c = \frac{\sigma_{TS}}{\langle {TS} \rangle} | NM_c = \frac{\sigma_{TS}}{\langle {TS} \rangle} | ||
\end{equation*} | \end{equation*} | ||
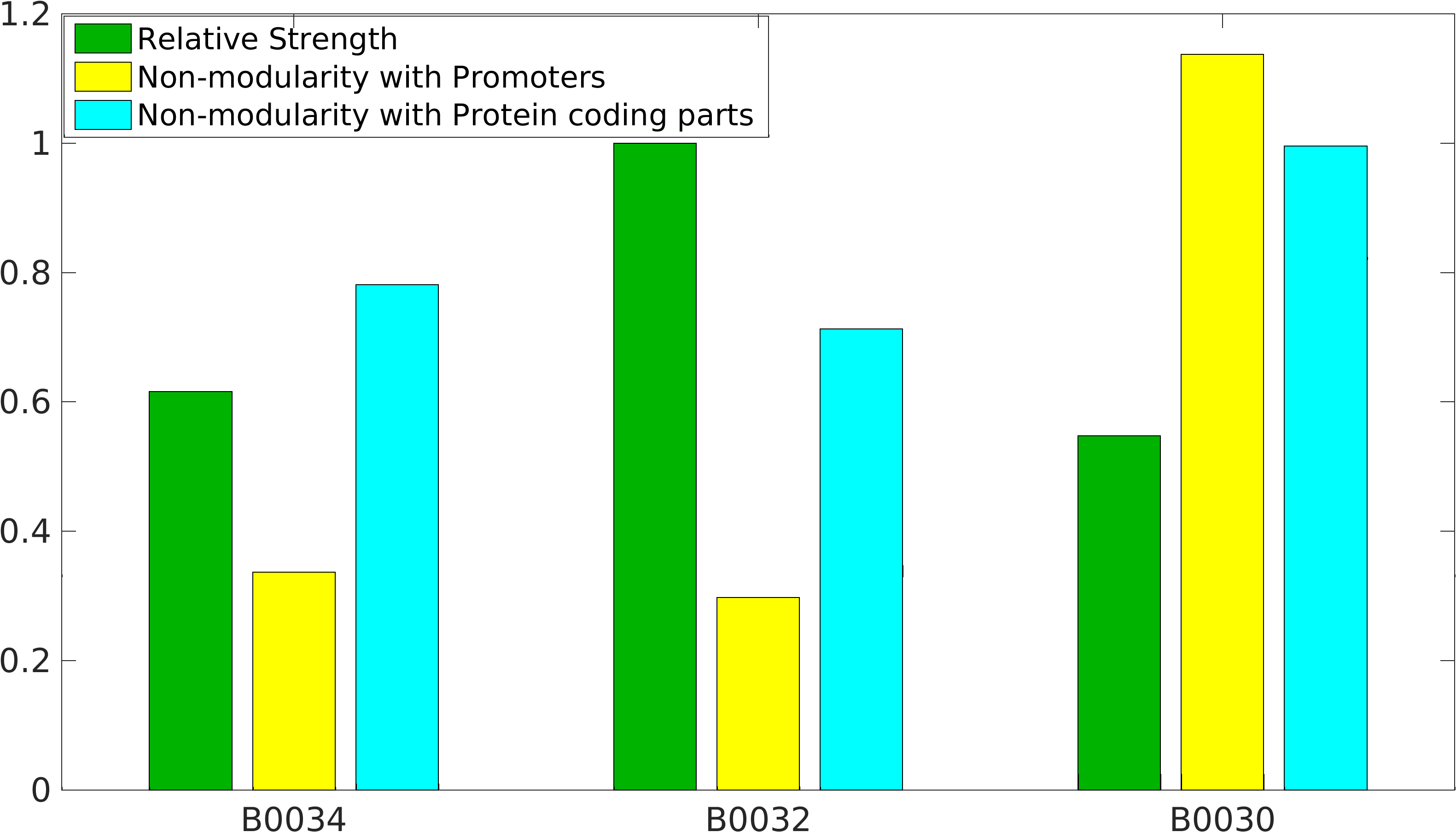
| − | + | where, '''NM<sub>p</sub>''' is non-modularity of RBS w.r.t. promoters; <br> | |
| + | '''NM<sub>c</sub>''' is non-modularity of RBS w.r.t. protein coding part; <br> '''NS''' is the array of native strength of RBS part with given promoters, <br> '''TS''' is the array of translational score of RBS part with given protein coding parts. | ||
== Optimization == | == Optimization == | ||
| − | + | Above model was optimized to compute the unknown variables, '''Native Strength of RBSs''' and '''codon preference matrix''', using the data from above mentioned paper. In MATLAB, <i>fmincon</i> function was used to minimize the sum of (\({TS_{model}-TS_{experiment})}^2\) for all 14137 constructs. After several iterations of optimization, we achieved following results. Optimization was done in MATLAB on a supercomputer facility at IIT Madras. | |
| − | + | Further, the system was optimized by removing 5%, 10% outliers, which were computed as the top scores in (\({TS_{model}-TS_{experiment})}^2\). | |
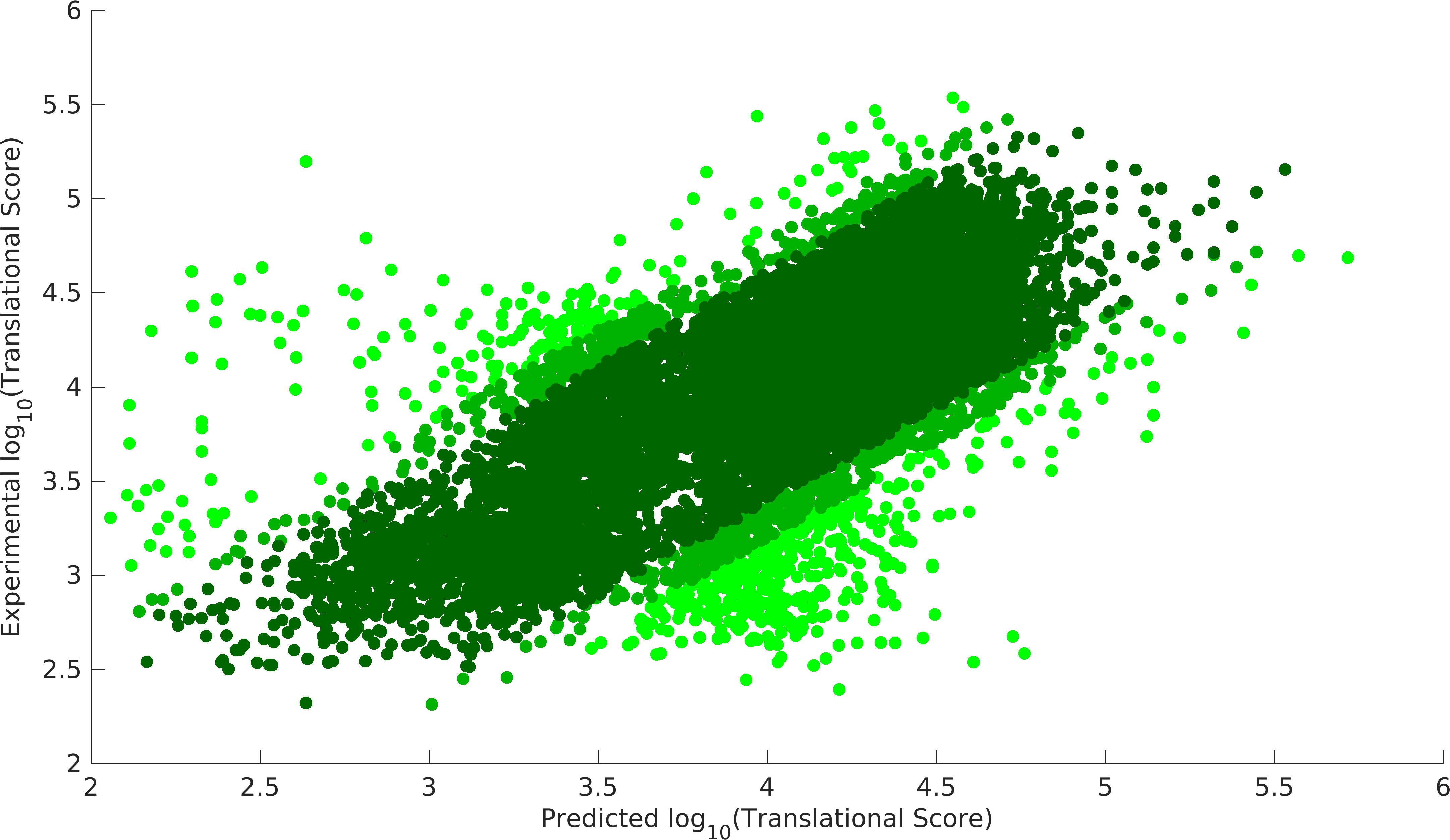
<gallery mode=nolines class=center widths=400px heights=230px caption="Validation of Model"> | <gallery mode=nolines class=center widths=400px heights=230px caption="Validation of Model"> | ||
| − | File:Igemiitm_exp_model2.png|Experiment model | + | File:Igemiitm_exp_model2.png|Experiment model, dark green 90% data, dark green+light dark green 95% data. |
| − | File:Igemiitm_exp_model1.png|Null model | + | File:Igemiitm_exp_model1.png|Null model, dark green 90% data, dark green+light dark green 95% data. |
</gallery> | </gallery> | ||
| Line 101: | Line 100: | ||
== Conclusion == | == Conclusion == | ||
| − | + | We could achieve a heuristic solution with a '''correlation of 0.87 with 90% of the data points''' for our experimental model, while null model gives us a correlation of 0.83 with 90% data points. Null model doesn't incorporate the feature of codon preference (C<sub>pref</sub>). As we see that codon preference feature improves our output, hence, it justifies the fact that codons can also vary translational score of RBS parts. Experimental model gives us the strength of promoter-RBS combined strength for 280 (2 promoters x 140 RBSs) combinations. This model provides a way to predict the variations in translational score of RBS parts unlike the existing tools. Using this model, users can get translational score for their expression systems. | |
= Noise in Devices = | = Noise in Devices = | ||
== Introduction == | == Introduction == | ||
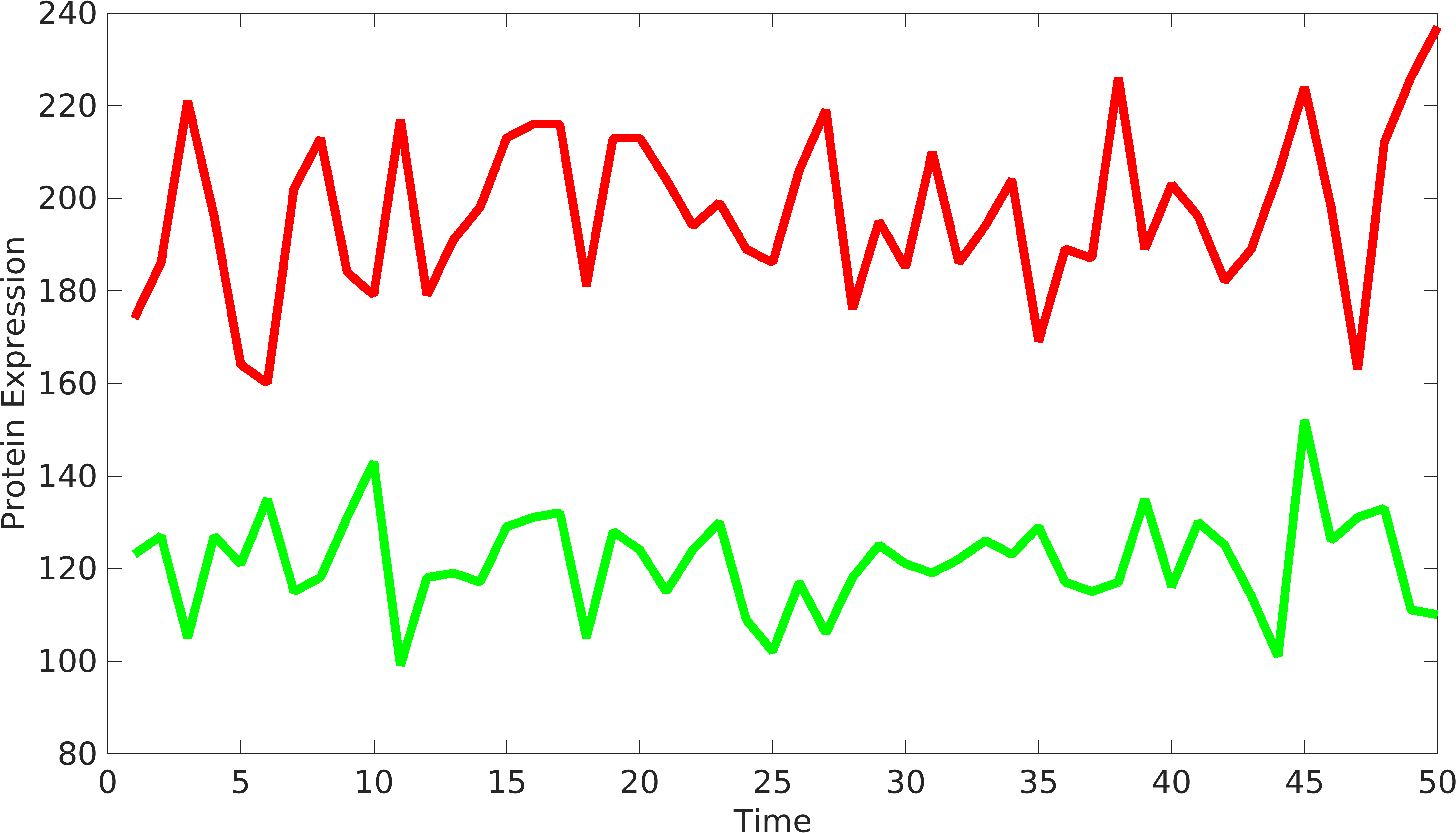
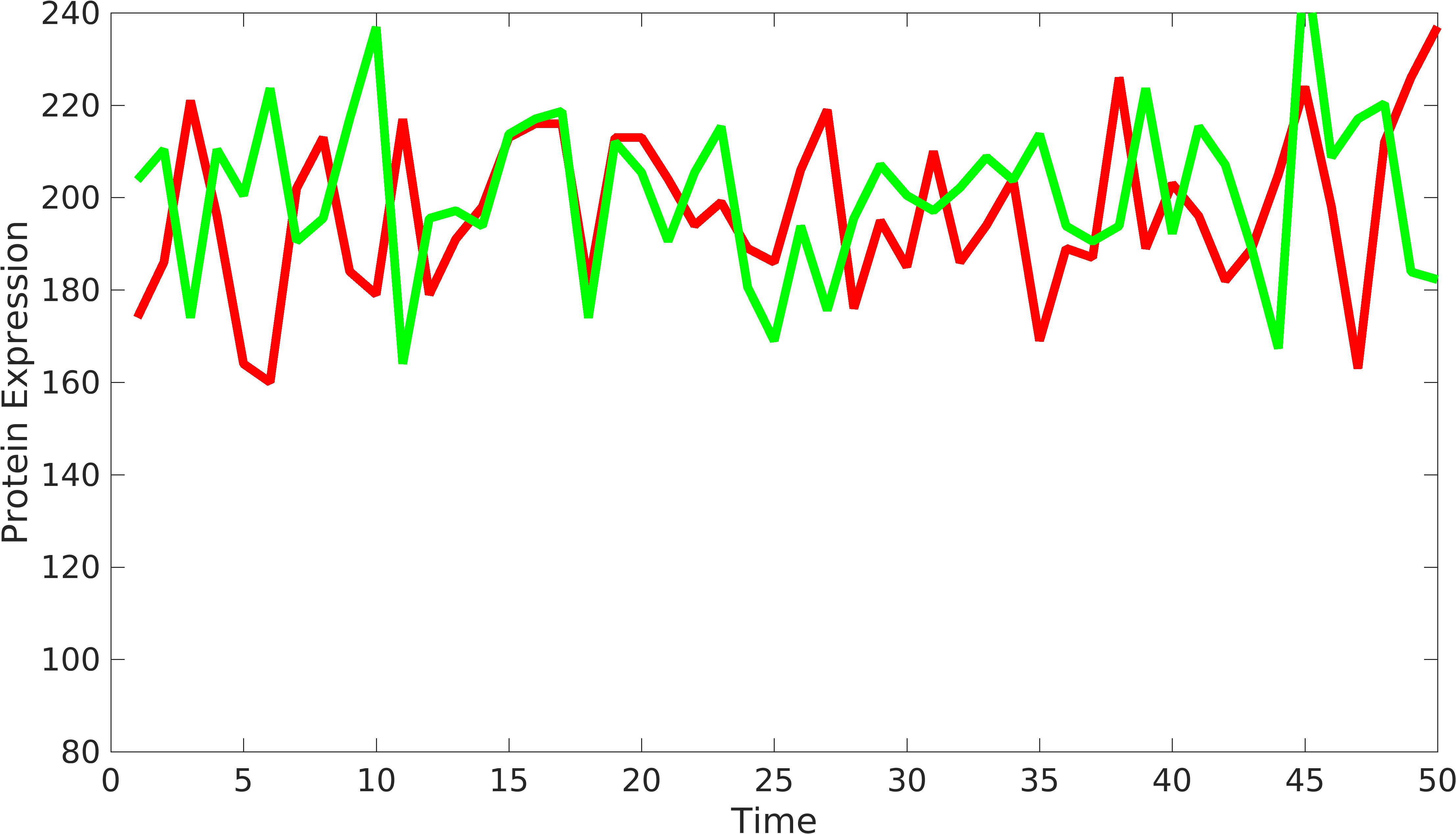
| − | + | In order to understand the behavior of device components, we need to have at least two signals coming from the device to understand the variations from '''intrinsic''' and '''extrinsic''' sources. Similarly, we can have two or more protein producing parts in complex biological devices, using which, we can understand the behavior of biological devices. [http://www.pnas.org/content/99/20/12795.short Elowtiz et al] has done significant work in understanding noise in biological devices. We have observed that if the mean value of one signal is bigger than the other signal, Elowitz formula doesn't give us accurate noise due to under-representation of variations present in low protein expressing device. | |
\begin{equation*} | \begin{equation*} | ||
| Line 118: | Line 117: | ||
== Solution == | == Solution == | ||
| + | To solve this problem, we have modified the current formula as follows: | ||
\begin{equation*} | \begin{equation*} | ||
gr_{fold}=\dfrac{\langle rfp \rangle}{\langle gfp \rangle} \\ | gr_{fold}=\dfrac{\langle rfp \rangle}{\langle gfp \rangle} \\ | ||
| Line 126: | Line 126: | ||
File:Noise_var2.png|Corrected Signals from biological device | File:Noise_var2.png|Corrected Signals from biological device | ||
</gallery> | </gallery> | ||
| − | |||
| − | |||
== References == | == References == | ||
| − | 1. Goodman, Daniel B., George M. Church, and Sriram Kosuri. "Causes and effects of N-terminal codon bias in bacterial genes." Science 342.6157 (2013): 475-479. | + | [http://science.sciencemag.org/content/342/6157/475 1.] Goodman, Daniel B., George M. Church, and Sriram Kosuri. "Causes and effects of N-terminal codon bias in bacterial genes." Science 342.6157 (2013): 475-479. |
{{IIT-Madras-Bottom/CSS}} | {{IIT-Madras-Bottom/CSS}} | ||
Latest revision as of 23:40, 19 October 2016
Contents
Modularity of RBS parts
Introduction
The non-modular nature of Ribosomal Binding Sites in bacteria is well known to the synthetic biology community. Most of the biological parts have been assigned a strength for their functionality. For example, Promoters have transcriptional score (number of RNA molecules per DNA molecule), RBSs have translational score (number of protein molecules per RNA molecule). Ideally, if we were to use a promoter and a RBS to produce a protein, we should get (transcriptional score times translational score) number of protein molecules. In bacterial cells, transcription and translation processes are coupled and can occur simultaneously. This is why, these process are not independent and, hence, not modular. Apart from this, RNA molecules consisting of RBS and first few codons may form secondary structures, which in turn reduce the translation efficiency. Also, rare codons have also been shown to influence translation efficiency.
Secondary structure's and codons' influence on translational score of RBS are overlapping as they are a result of A, U, G, C combinations. Therefore, it is important to decouple both effects to unravel underlying patterns.
We have successfully validated an empirical model to predict variations in protein expression levels, which could help future iGEM teams. Here, we represent a thorough description of our work.
Methodology
The dataset from "Causes and effects of N-terminal codon bias in bacterial genes" paper was taken. Protein expression Data was available for following constructs : 2 promoters x 3 RBSs x 1781 (137x13) sfGFP variants in first 11 codons at N-terminal (3 RBS parts were B0034, B0032, B0030) and 2 promoter x 137 natural RBSs x 13 sfGFP variants in first 11 codons at N-terminal (2 Promoters were J23100 & J23108)
Hypothesis and Algorithm
At the beginning, we hypothesized following things based on the information available in literature:
1. Expression is inversely proportional to the stability of secondary structure of mRNA near RBS part.
2. Rare codons present in first 11 codons of proteins have the ability to increase or decrease the translational score of RBS parts.
3. Each RBS part has a native strength irrespective of the promoter and protein coding part it can be used with.
We designed an algorithm to compute the translational score of a given construct(which expresses a protein) in the following way: \begin{equation*} TS = \dfrac{NS*C_{pref}}{1+dG} + \alpha \end{equation*}
\begin{equation*} C_{pref}= C_{1}*C_{2}*C_{3}*...*C_{11}*C_{sfGFP} \end{equation*}
Objective Function: minimize \(\sum \mid TS_{model}-TS_{experiment} \mid\)
Outlier Removal: top scores in \(\mid TS_{model}-TS_{experiment} \mid\)
where \(C_{i}\) is the codon preference of codon present at \(i^{th}\) position, \(C_{sfGFP}\) a constant for sfGFP protein codons,
TS : Translational Score of RBS part,
NS : Native Strength of RBS part, which is equal to TS at \(\delta\)G=0, \(C_{pref}\)=1;
\(\delta\)G : Stability of RNA strand consisting of RBS and first 11 codon of protein,
\(\alpha\) is a constant.
Quantification of Non-modularity
As previously mentioned, RBS's have been found to be non-modular with respect to promoter and protein coding parts. A quantification of modularity would enable us to screen better RBS parts to make high order complex genetic circuits in high-throughput manner.
\begin{equation*}
NM_p = \frac{\sigma_{NS}}{\langle {NS} \rangle} \\
NM_c = \frac{\sigma_{TS}}{\langle {TS} \rangle}
\end{equation*}
where, NMp is non-modularity of RBS w.r.t. promoters;
NMc is non-modularity of RBS w.r.t. protein coding part;
NS is the array of native strength of RBS part with given promoters,
TS is the array of translational score of RBS part with given protein coding parts.
Optimization
Above model was optimized to compute the unknown variables, Native Strength of RBSs and codon preference matrix, using the data from above mentioned paper. In MATLAB, fmincon function was used to minimize the sum of (\({TS_{model}-TS_{experiment})}^2\) for all 14137 constructs. After several iterations of optimization, we achieved following results. Optimization was done in MATLAB on a supercomputer facility at IIT Madras. Further, the system was optimized by removing 5%, 10% outliers, which were computed as the top scores in (\({TS_{model}-TS_{experiment})}^2\).
- Validation of Model
Results
We found that some codons favor the translation process, while some of this do not. Following is a list of codons, which favor the translation process:
| Codon | AAA | AAT | AGA | AGC | AGT | ATA | GAT | GGC | GGG | GGT | GTA | TCA | TCC | TCT | TGC |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Amino Acid | K | N | R | S | S | I | D | G | G | G | V | S | S | S | C |
| Preference Value | 1.17 | 1.23 | 1.15 | 1.13 | 1.21 | 1.14 | 1.13 | 1.19 | 1.19 | 1.21 | 1.14 | 1.14 | 1.13 | 1.19 | 1.19 |
Following is a list of codons, which reduces the translation efficiency:
| Codon | CAC | CGC | CTC | GTC | TTC |
|---|---|---|---|---|---|
| Amino Acid | H | R | L | V | F |
| Preference Value | 0.9768 | 0.9862 | 0.979 | 0.997 | 0.993 |
A complete list of codons and their preference values are here
Conclusion
We could achieve a heuristic solution with a correlation of 0.87 with 90% of the data points for our experimental model, while null model gives us a correlation of 0.83 with 90% data points. Null model doesn't incorporate the feature of codon preference (Cpref). As we see that codon preference feature improves our output, hence, it justifies the fact that codons can also vary translational score of RBS parts. Experimental model gives us the strength of promoter-RBS combined strength for 280 (2 promoters x 140 RBSs) combinations. This model provides a way to predict the variations in translational score of RBS parts unlike the existing tools. Using this model, users can get translational score for their expression systems.
Noise in Devices
Introduction
In order to understand the behavior of device components, we need to have at least two signals coming from the device to understand the variations from intrinsic and extrinsic sources. Similarly, we can have two or more protein producing parts in complex biological devices, using which, we can understand the behavior of biological devices. [http://www.pnas.org/content/99/20/12795.short Elowtiz et al] has done significant work in understanding noise in biological devices. We have observed that if the mean value of one signal is bigger than the other signal, Elowitz formula doesn't give us accurate noise due to under-representation of variations present in low protein expressing device.
\begin{equation*} Noise_{int}=\frac{\langle {rfp-gfp} \rangle^2}{2*\langle gfp \rangle* \langle rfp \rangle};\\ if \langle rfp \rangle > \langle gfp \rangle; Noise_{int} = \frac{{\langle rfp \rangle}^2}{2*\langle gfp \rangle*\langle rfp \rangle}; \\ Noise_{int} = \frac{\langle {rfp} \rangle}{2*\langle gfp \rangle}; \end{equation*}
Solution
To solve this problem, we have modified the current formula as follows: \begin{equation*} gr_{fold}=\dfrac{\langle rfp \rangle}{\langle gfp \rangle} \\ Noise_{int}=\frac{\langle{rfp-gfp*gr_{fold}}\rangle^2}{2*\langle gfp \rangle*\langle rfp \rangle*gr_{fold}};\\ \end{equation*}
References
[http://science.sciencemag.org/content/342/6157/475 1.] Goodman, Daniel B., George M. Church, and Sriram Kosuri. "Causes and effects of N-terminal codon bias in bacterial genes." Science 342.6157 (2013): 475-479.