Difference between revisions of "Team:UFAM-UEA Brazil/MathModeling"
Manickchand (Talk | contribs) |
Manickchand (Talk | contribs) |
||
| Line 30: | Line 30: | ||
<p>where G is the inactive form of gene repressed by merR, and X is its active form. Through the law of mass action we derive the diferential equation</p> | <p>where G is the inactive form of gene repressed by merR, and X is its active form. Through the law of mass action we derive the diferential equation</p> | ||
| − | <p>(1)<img src="https://static.igem.org/mediawiki/2016/6/6b/UFAM_UEA_Team_math_%283%29.png" width=250 height= | + | <p>(1)<img src="https://static.igem.org/mediawiki/2016/6/6b/UFAM_UEA_Team_math_%283%29.png" width=250 height=60/> <p> |
<p>At the equillibrium state, ie. <img src=" | <p>At the equillibrium state, ie. <img src=" | ||
Revision as of 20:18, 18 October 2016
MODEL OF RFP PRODUCTION
1. Modelling
We want to characterize the promoter’s velocity of expression due to presence of mercury, so we will attach an RFP gene to it to produce.
First we will model the production of RFP due to Hg2+ at stationary time phase with this configuration. Then we add the initial phase consideration
1.1 Stationary time phase.
The GMO we have is:
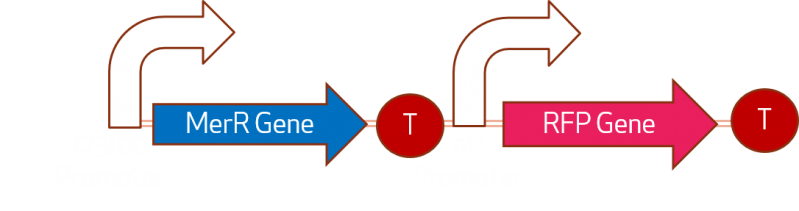
Where MerR is a repressor and releases when H2+ is presented in the interior of the cell, we will note this amount as Hgin and the exterior as Hgout. And Promoter nP is the promoter which velocity we want to characterize. The activation of the gene in the pressence of Hgin is represented like:
where G is the inactive form of gene repressed by merR, and X is its active form. Through the law of mass action we derive the diferential equation
(1)
At the equillibrium state, ie. 
, we have that the proportion of genes in the activated gene is
