Team:UFAM-UEA Brazil/MathModeling
MODEL OF RFP PRODUCTION
1. Modelling
We want to characterize the promoter’s velocity of expression due to presence of mercury, so we will attach an RFP gene to it to produce.
First we will model the production of RFP due to Hg2+ at stationary time phase with this configuration. Then we add the initial phase consideration
1.1 Stationary time phase.
The GMO we have is:
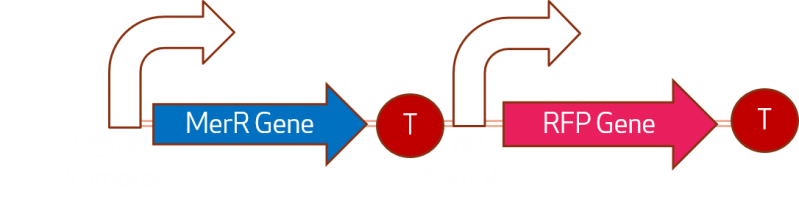
Where MerR is a repressor and releases when H2+ is presented in the interior of the cell, we will note this amount as Hgin and the exterior as Hgout. And Promoter nP is the promoter which velocity we want to characterize. The activation of the gene in the pressence of Hgin is represented like:
where G is the inactive form of gene repressed by merR, and X is its active form. Through the law of mass action we derive the diferential equation
(1)
At the equillibrium state, ie. 
, we have that the proportion of genes in the activated gene is
(2)
Where 
So this is the average production rate of a typical gene, so the average mRNA production will be
(3)
Where α is the production of mRNA due to the stochastic nature of the binding of merR for repressing the RNA Polymerase and δ1 is the degradation factor of mRNA. The reaction for production of RFP from mRNA is
so we derive the diferential equation
(4)
where δ2 is the degradation constant of [RFP]. The variation of exterior mercury is
from here we derive the differential equation
(5)
As the interior mercury is used by the inactive form of the gene, the variation of Hgin2+ is
(6)
To solve this system we will assume that the permeability of the cell memebrane to mercury is instantaneus then we have that 
then 
so we have that the variation of the interior mercury is
(7)
And assume that mRNA is at Quasi-Steady state, ie. 
, then we have
that the amount of mRNA is
(8)
Then we have that the velocity of production of RFP is
(9)
So we will also assume that the degradation of RFP is very slow, δ2 = 0, and also the stochastic production of mRNA is very slow, α = 0. Then finaly we have that the production of RFP is
(10)
Where 
1.2. Initial phase. Since bacteria grow exponentially, it is often useful to plot the logarithm of the relative population size [Y = ln(N/N0)] against time .So lets use the Gompertz equation to model this. The three phases of the growth curve can be described by three parameters: the maximum specific growth rate, µm is defined as the tangent in the inflection point; the lag time, λ, is defined as the x-axis intercept of this tangent; and the asymptote [A = ln(N/N0)] is the maximal value reached. Here we are not considering the death rate.[1]
(11)
Lets add that the amount of bacteria changes to our model. So we have more bacteria. As Vmáx depends on the amount of bacteria, so we can propose that a single bacteria has a velocity 
production of RFP per unit of time and then
(12)
So our model now is
(12)
Here we are assuming that when a bacter appears it alredy has all the properties necessary to work, so that delay is inside the growing time.
Where M is the free mercury and C∗ is the mercury linked with the complex C, kC is the rate of production of the complex and δC is the rate of degradation of the complex. As we put the bactery with the mercury after some hours we can assume that the cell are full populated so we have that [CT] = [C] + [C∗] then we only need to know how vary [C∗] because [CT] is constant.
(1)
Also as the total concentration of mercury does not change we have that M0 = [M]+[C*] where [M] is the concentration of free mercury, [C*] is the concentration of the mercury linked with Phitoquelatin that is linked with Omp-A per cell.
(2)
We can assume that the rate of splitting of the complex C∗ is 0, because Mercury and Phitoquelatin have very hight affinity.
(3)
References:
[1] MH Zwietering, Il Jongenburger, FM Rombouts, and K Van’t Riet. Modeling of the bacterial growth curve. Applied and environmental microbiology, 56(6):1875–1881, 1990
Where M is the free mercury and C∗ is the mercury linked with the complex C, kC is the rate of production of the complex and δC is the rate of degradation of the complex. As we put the bactery with the mercury after some hours we can assume that the cell are full populated so we have that [CT] = [C] + [C∗] then we only need to know how vary [C∗] because [CT] is constant.
(1)
Also as the total concentration of mercury does not change we have that M0 = [M]+[C*] where [M] is the concentration of free mercury, [C*] is the concentration of the mercury linked with Phitoquelatin that is linked with Omp-A per cell.
(2)
We can assume that the rate of splitting of the complex C∗ is 0, because Mercury and Phitoquelatin have very hight affinity.
(3)
References:
[1] MH Zwietering, Il Jongenburger, FM Rombouts, and K Van’t Riet. Modeling of the bacterial growth curve. Applied and environmental microbiology, 56(6):1875–1881, 1990
