Team:UT-Tokyo/Model
Modeling Overview
We estimated the possibility that the genetic circuit works as intended by constructing mathematical modeling. First, we simulated time series of concentration of each fluorescent protein to find parameters which establish expression loops of them. We also mathematically analyzed the stability of the expression loops, and the parameters which make the loops stable were found with this analysis. We conducted parameter fitting with the data which we got from experiment, in order to estimate the parameters that we used in our simulation. The parameters that we could not obtain from the experiment were estimated from literature.
Simulation of Time Series of Concentration of Fluorescent Protein
Aim
We ran the simulation of the transcription and translation for two reasons. The first one is to make sure that our project is not theoretically impossible. In other words, if we can find the parameter sets which establish the loop of gene expression, it means our project is theoretically feasible. And also it is expected that we can get the insight for improving our design of the genetic circuit using this simulation.
The second one is to check whether genetic circuit works as intended under the given condition when parameters are obtained from experiment. If there is a tool which can calculates the behavior of genetic circuit with any parameter sets inputted and outputs a graph indicating time series of concentration of fluorescent proteins, it is useful for judging whether genetic circuit works as intended when we get the actual parameters from experiments or literature. So we developed the tool.
Method
We described the behavior of the genetic circuit by differential equations and developed a tool solving the differential equations with Euler's method. We judged from the graph outputted by the tool under various parameter sets whether the gene expression loop was generated as intended. First, the meaning of each variable is indicated in the table below.
| variables | character |
| sigma-factor A,B,C | $[\sigma_A], [\sigma_B], [\sigma_C]$ |
| anti-sigma factor, A, B, C | $[\sigma_{-A}], [\sigma_{-B}], [\sigma_{-C}]$ |
| mRNA of sigma factor A, B, C without toehold switch | $R_A, R_B, R_C$ |
| mRNA of anti-sigma-factor A, B,C without toehold switch | $R_{-A}, R_{-B}, R_{-C}$ |
| mRNA of sigma factor A, B, C with toehold switch | $R_{td, A}, R_{td, B}, R_{td, C}$ |
| triggerRNA | $[\mathrm{triggerRNA}]$ |
| arabinose | $[\mathrm{arabinose}]$ |
| immature GFP, RFP, CFP | $[\mathrm{imGFP}], [\mathrm{imRFP}], [\mathrm{imCFP}]$ |
| mature GFP, RFP, CFP | $[\mathrm{GFP}], [\mathrm{RFP}], [\mathrm{CFP}]$ |
| mRNA of GFP, RFP, CFP | $R_{GFP}, R_{RFP}, R_{CFP}$ |
Let us explain how to make differential equations expressing behavior of genetic circuit. First, we will talk about transcription control by sigma-factors. The transcription rate of a gene, under a certain promoter which starts transcription by binding a certain sigma factor, is proportional to the following formula including the Hill equation when no anti-sigma-factors exist. $$\frac{[\sigma]}{K + [\sigma]}$$ $K$ is the dissociation constant between sigma-factor and promoter.
If anti-sigma-factor exists, it inhibits the activity of sigma-factor. Therefore, the ratio of inhibited sigma-factor to all sigma-factors is expressed by the following formula including the Hill equation. $$\frac{[anti-{\sigma}]}{K’ + [anti-{\sigma}]}$$ $K’$ means the dissociation constant between sigma-factor and anti-sigma-factor.
It follows that the gene transcription rate of sigma-promoter is proportional to the Hill equation of activated sigma-factor, $$ [\sigma] \frac{1 - \frac{[anti-{\sigma}]}{K’ + [anti-{\sigma}]}}{ K + [\sigma](1 - \frac{[anti-{\sigma}]}{K’ + [anti-{\sigma}]})} $$ The transcription of the mRNA of sigma-factor A under pbad can also be described using Hill equation.
The ratio of mRNA which is translated into proteins to whole mRNA with toehold switch (the rate of mRNA whose hairpin structure around RBS is broken by triggerRNA) is proportional to the following formula including the Hill equation. $$[\mathrm{triggerRNA}]/(K’’ + [\mathrm{triggerRNA}])$$ $K’’$ means the dissociation constant between triggerRNA and hairpin structure around RBS. The decomposition rate of a certain substance whose half-life is HL is log2/HL. Here, we assume that the maturation rate of a certain fluorescent protein is proportional to the concentration of it. The proportionality constant of maturation rate of a certain fluorescent protein whose maturation time is MT is log2/MT, on the analogy of decomposition rate. We represented the activation of Pnrd which is the key of this circuit as a short pulse wave occurring once a cell cycle. Without considering activation of Pnrd in detail, we represented it as the change of way to express of triggerRNA. Paying attention to these policies, we expressed the behavior of genetic circuit by 26 nonlinear differential equations below.
$$\frac{d[\sigma_A]}{dt}= \alpha \cdot\left(R_A+\frac{R_{td,A}\cdot [\mathrm{triggerRNA}]}{K^{\prime\prime}+[\mathrm{triggerRNA}]}\right)-\frac{\ln2}{\mathrm{HL}_{\sigma_A}}\cdot[\sigma_A]$$ $$\frac{d[\sigma_B]}{dt}= \alpha\cdot \left(R_B+\frac{R_{td,B}\cdot [\mathrm{triggerRNA}]}{K^{\prime\prime}+[\mathrm{triggerRNA}]}\right)-\frac{\ln2}{\mathrm{HL}_{\sigma_B}}\cdot[\sigma_B]$$ $$\frac{d[\sigma_C]}{dt}= \alpha\cdot \left(R_C+\frac{R_{td,C}\cdot [\mathrm{triggerRNA}]}{K^{\prime\prime}+[\mathrm{triggerRNA}]}\right)-\frac{\ln2}{\mathrm{HL}_{\sigma_C}}\cdot[\sigma_C]$$ $$\frac{d[\sigma_{\mbox{-}A}]}{dt}= \alpha\cdot R_{\mbox{-}A}-\frac{\ln2}{\mathrm{HL}_{\sigma_{\mbox{-}A}}}[\sigma_{\mbox{-}A}]$$ $$\frac{d[\sigma_{\mbox{-}B}]}{dt}= \alpha\cdot R_{\mbox{-}B}-\frac{\ln2}{\mathrm{HL}_{\sigma_{\mbox{-}B}}}[\sigma_{\mbox{-}B}]$$ $$\frac{d[\sigma_{\mbox{-}C}]}{dt}= \alpha\cdot R_{\mbox{-}C}-\frac{\ln2}{\mathrm{HL}_{\sigma_{\mbox{-}C}}}[\sigma_{\mbox{-}C}]$$ $$\frac{dR_A}{dt}= k\cdot \mathrm{C}_{low}\cdot \frac{[\sigma_A]\cdot(1-\frac{[\sigma_{\mbox{-}A}]}{K'_a+[\sigma_{\mbox{-}A}]})}{K_a+[\sigma_A]\cdot\left(1-\frac{[\sigma_{\mbox{-}A}]}{K'_a+[\sigma_{\mbox{-}A}]}\right)}+\frac{c_{araC}\cdot\frac{[\mathrm{arabinose}]}{K'_{araC}+[\mathrm{arabinose}]}}{K_{araC}+c_{araC}\cdot\frac{[\mathrm{arabinose}]}{K'_{araC}+[\mathrm{arabinose}]}}-\frac{\ln2}{\mathrm{HL}_{RNA}}\cdot R_A$$ $$\frac{dR_B}{dt}= k\cdot \mathrm{C}_{low}\cdot \frac{[\sigma_B]\cdot(1-\frac{[\sigma_{\mbox{-}B}]}{K'_b+[\sigma_{\mbox{-}B}]})}{K_b+[\sigma_B]\cdot\left(1-\frac{[\sigma_{\mbox{-}B}]}{K'_b+[\sigma_{\mbox{-}B}]}\right)}-\frac{\ln2}{\mathrm{HL}_{RNA}}\cdot R_B$$ $$\frac{dR_C}{dt}= k\cdot \mathrm{C}_{low}\cdot \frac{[\sigma_C]\cdot(1-\frac{[\sigma_{\mbox{-}C}]}{K'_c+[\sigma_{\mbox{-}C}]})}{K_c+[\sigma_C]\cdot\left(1-\frac{[\sigma_{\mbox{-}C}]}{K'_c+[\sigma_{\mbox{-}C}]}\right)}-\frac{\ln2}{\mathrm{HL}_{RNA}}\cdot R_C$$ $$\frac{dR_{\mbox{-}A}}{dt}= k\cdot \mathrm{C}_{high}\cdot \frac{[\sigma_B]\cdot(1-\frac{[\sigma_{\mbox{-}B}]}{K'_b+[\sigma_{\mbox{-}B}]})}{K_b+[\sigma_B]\cdot\left(1-\frac{[\sigma_{\mbox{-}B}]}{K'_b+[\sigma_{\mbox{-}B}]}\right)}-\frac{\ln2}{\mathrm{HL}_{RNA}}\cdot R_{\mbox{-}A}$$ $$\frac{dR_{\mbox{-}B}}{dt}= k\cdot \mathrm{C}_{high}\cdot \frac{[\sigma_C]\cdot(1-\frac{[\sigma_{\mbox{-}C}]}{K'_c+[\sigma_{\mbox{-}C}]})}{K_c+[\sigma_C]\cdot\left(1-\frac{[\sigma_{\mbox{-}C}]}{K'_c+[\sigma_{\mbox{-}C}]}\right)}-\frac{\ln2}{\mathrm{HL}_{RNA}}\cdot R_{\mbox{-}B}$$ $$\frac{dR_{\mbox{-}C}}{dt}= k\cdot \mathrm{C}_{high}\cdot\frac{ [\sigma_A]\cdot(1-\frac{[\sigma_{\mbox{-}A}]}{K'_a+[\sigma_{\mbox{-}A}]})}{K_a+[\sigma_A]\cdot\left(1-\frac{[\sigma_{\mbox{-}A}]}{K'_a+[\sigma_{\mbox{-}A}]}\right)}-\frac{\ln2}{\mathrm{HL}_{RNA}}\cdot R_{\mbox{-}C}$$ $$\frac{dR_{td,A}}{dt}= k\cdot \mathrm{C}_{low}\cdot \frac{[\sigma_C]\cdot(1-\frac{[\sigma_{\mbox{-}C}]}{K'_a+[\sigma_{\mbox{-}C}]})}{K_c+[\sigma_C]\cdot\left(1-\frac{[\sigma_{\mbox{-}C}]}{K'_c+[\sigma_{\mbox{-}C}]}\right)}-\frac{\ln2}{\mathrm{HL}_{RNA}}\cdot R_{td,A}$$ $$\frac{dR_{td,B}}{dt}= k\cdot \mathrm{C}_{low}\cdot \frac{[\sigma_A]\cdot(1-\frac{[\sigma_{\mbox{-}A}]}{K'_a+[\sigma_{\mbox{-}A}]})}{K_a+[\sigma_A]\cdot\left(1-\frac{[\sigma_{\mbox{-}A}]}{K'_a+[\sigma_{\mbox{-}A}]}\right)}-\frac{\ln2}{\mathrm{HL}_{RNA}}\cdot R_{td,B}$$ $$\frac{dR_{td,C}}{dt}= k\cdot \mathrm{C}_{low}\cdot \frac{[\sigma_B]\cdot(1-\frac{[\sigma_{\mbox{-}B}]}{K'_b+[\sigma_{\mbox{-}B}]})}{K_b+[\sigma_B]\cdot\left(1-\frac{[\sigma_{\mbox{-}B}]}{K'_b+[\sigma_{\mbox{-}B}]}\right)}-\frac{\ln2}{\mathrm{HL}_{RNA}}\cdot R_{td,C}$$ $$\frac{d[\mathrm{triggerRNA}]}{dt}= k\cdot c_{low}-\frac{\ln2}{\mathrm{HL}_{RNA}}\cdot[\mathrm{triggerRNA}]\ \textrm{(when Pnrd is on)}$$ $$-\frac{\ln2}{\mathrm{HL}_{RNA}}\cdot [\mathrm{triggerRNA}] \ \textrm{(when Pnrd is off)}$$ $$\frac{d[\mathrm{arabinose}]}{dt}= -\frac{\ln2}{\mathrm{HL}_{arabinose}}\cdot [\mathrm{arabinose}]$$ $$\frac{d[\mathrm{imGFP}]}{dt}= \alpha\cdot [R_{\mathrm{GFP}}]-\frac{\ln2}{\mathrm{MT}_{GFP}}\cdot [\mathrm{imGFP}]-\frac{\ln2}{\mathrm{HL}_{imGFP}}\cdot [\mathrm{imGFP}]$$ $$\frac{d[\mathrm{imRFP}]}{dt}= \alpha\cdot [R_{\mathrm{RFP}}]-\frac{\ln2}{\mathrm{MT}_{RFP}}\cdot [\mathrm{imRFP}]-\frac{\ln2}{\mathrm{HL}_{imRFP}}\cdot [\mathrm{imRFP}]$$ $$\frac{d[\mathrm{imCFP}]}{dt}= \alpha\cdot [R_{\mathrm{CFP}}]-\frac{\ln2}{\mathrm{MT}_{CFP}}\cdot [\mathrm{imCFP}]-\frac{\ln2}{\mathrm{HL}_{imCFP}}\cdot [\mathrm{imCFP}]$$ $$\frac{d[\mathrm{GFP}]}{dt}= \frac{\ln2}{\mathrm{MT}_{GFP}}\cdot [\mathrm{imGFP}]-\frac{\ln2}{\mathrm{HL}_{GFP}}\cdot [\mathrm{GFP}]$$ $$\frac{d[\mathrm{RFP}]}{dt}= \frac{\ln2}{\mathrm{MT}_{RFP}}\cdot [\mathrm{imRFP}]-\frac{\ln2}{\mathrm{HL}_{RFP}}\cdot [\mathrm{RFP}]$$ $$\frac{d[\mathrm{CFP}]}{dt}= \frac{\ln2}{\mathrm{MT}_{CFP}}\cdot [\mathrm{imCFP}]-\frac{\ln2}{\mathrm{HL}_{CFP}}\cdot [\mathrm{CFP}]$$ $$\frac{dR_{\mathrm{GFP}}}{dt}= k\cdot \mathrm{C}_{low}\cdot \frac{[\sigma_A]\cdot(1-\frac{[\sigma_{\mbox{-}A}]}{K'_a+[\sigma_{\mbox{-}A}]})}{K_a+[\sigma_A]\cdot\left(1-\frac{[\sigma_{\mbox{-}A}]}{K'_a+[\sigma_{\mbox{-}A}]}\right)}-\frac{\ln2}{\mathrm{HL}_{RNA}}\cdot R_{\mathrm{GFP}}$$ $$\frac{dR_{\mathrm{RFP}}}{dt}= k\cdot \mathrm{C}_{low}\cdot \frac{[\sigma_B]\cdot(1-\frac{[\sigma_{\mbox{-}B}]}{K'_b+[\sigma_{\mbox{-}B}]})}{K_b+[\sigma_B]\cdot\left(1-\frac{[\sigma_{\mbox{-}B}]}{K'_b+[\sigma_{\mbox{-}B}]}\right)}-\frac{\ln2}{\mathrm{HL}_{RNA}}\cdot R_{\mathrm{RFP}}$$ $$\frac{dR_{\mathrm{CFP}}}{dt}= k\cdot \mathrm{C}_{low}\cdot \frac{[\sigma_C]\cdot(1-\frac{[\sigma_{\mbox{-}C}]}{K'_c+[\sigma_{\mbox{-}C}]})}{K_c+[\sigma_C]\cdot\left(1-\frac{[\sigma_{\mbox{-}C}]}{K'_c+[\sigma_{\mbox{-}C}]}\right)}-\frac{\ln2}{\mathrm{HL}_{RNA}}\cdot R_{\mathrm{CFP}}$$
Each parameter has each meaning as follows.
| parameters | character |
| proportionality constant of transcription rate | $k$ |
| proportional constant of translation speed | $\alpha$ |
| concentration of low copy plasmid | $C_{low}$ |
| concentration of high copy plasmid | $C_{high}$ |
| concentration of araC | $c_{araC}$ |
| the dissociation constant between sigma-factor and sigma-promoter | $K$ |
| the dissociation constant between araC and pbad operator | $K_{araC}$ |
| the dissociation constant between sigma-factor and anti-sigma-factor | $K^{\prime}$ |
| the dissociation constant between araC and arabinose | $K^{\prime}_{araC}$ |
| the dissociation constant between toehold switch and triggerRNA | $K^{\prime\prime}$ |
| half-life time of each substance | $\mathrm{HL}$ |
| maturation time of fluorescent protein | $\mathrm{MT}$ |
We assume that the half life of every RNA is same.
Basically, we gave positive value to initial concentration of arabinose, and gave zero to other initial values. We also conducted another simulation that positive values were given to other initial values to make sure that the initial state makes little difference to the result of simulation.
We applied two ideas to imitate genuine environment in living E. coli instead of just solving the differential equation. First one is introduction of Gaussian noise into simulation. In real bacteria cell, the rate of transcription and translation is not constant and it fluctuates a little. To examine the influence of this fluctuation to the result of simulation, we added random numbers that follow normal distribution to transcription and translation rate every step of Euler approximation.
Second one is introduction of delay of transcription and translation. For instance, it takes some time (put this as s hours) to synthesize one molecule of mRNA. Therefore, the increase rate of concentration of mRNA at T hours does not depend on a concentration of sigma-factor and anti-sigma-factor at T hours, but on at (T - s) hours.
Similarly, it also takes some time (put this as t hours) to synthesize one molecule of protein from mRNA. Therefore, the increase rate of concentration of the protein at T hours does not depend on concentration of mRNA at T hours, but on at (T - t) hours.
Consequently, we adopted abnormal Euler method which calculates the concentration of each substance at T, using concentration data of s or t hours ago. s and t are also parameters.
File:T--UT-Tokyo--Modeling--Simulation.zip
This is a source code of our tool which calculates behavior of the genetic circuit by solving these differential equations paying attention to these policies. This code runs a simulation of 30 generations of E. coli. The unit of time is hour and the unit of concentration is μM. One step of Euler approximating is 0.72 second.
Using this tool, we tried various parameter sets and searched for the parameter sets which make the expression loop successful. The order of each parameter is estimated referring to various literature (Parameter Estimation).
Also, we estimated parameters using the data obtained from our experiment (Parameter Fitting).
Result and Discussion
The model of the genetic circuit we designed generated correct loops under certain parameters sets and did not generate under other parameters sets.
Therefore, it seems theoretically possible for the genetic circuit designed in our project to behave as expected.
For example, the result of simulation using certain parameters (Parameter Set A in Section 4) is below.
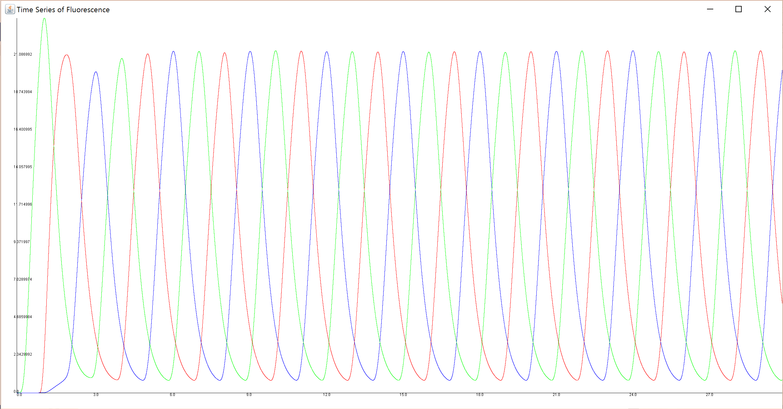The code (samplechart.java) simulates behavior of 30 generations, so if ten loops of three generations (GFP dominant, RFP dominant and CFP dominant) appears, it means the genetic circuit works successfully. In this graph, there are ten peaks of GFP concentration (green curve), RFP concentration (red curve) and CFP concentration (blue curve). Therefore, it is appropriate to judge that the loop works as designed.
On the other hand, under certain different parameters (Parameter Set B in Section 4), the result of this simulation became the graph below.
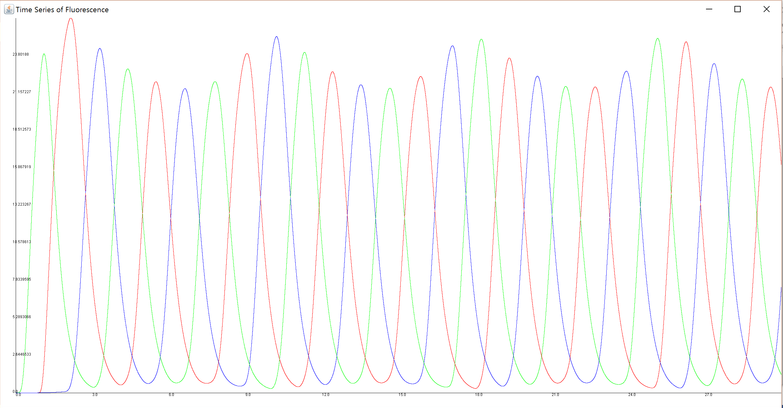In this graph, each curve does not have just ten peaks. It follows that under this parameter set, the loop designed does not work, that is, the genetic circuit does not function as intended.
Stability Analysis of Expression Loops
Aim
We judged whether the expression loops were generated successfully or not, on the basis of the graph outputted by our simulation tool mentioned in the former section. However, this way of judgement is objectively doubtful slightly since there are not mathematical criteria to judge. Also, judging with our human eye is too laborious to analyze exhaustively. To show the stability of gene expression loop requires more mathematical evidence. We conducted an objective analysis of the stability of the loop. If a tool is developed which outputs the result of stability analysis according to the inputted parameters, it helps us to judge the stability of genetic circuit (whether the loop is stable independently of initial states and perturbation of concentration of the factors) under various parameter sets and choose the factor to use in the genetic circuit. So we developed the tool.
Method
We developed a tool which judges the stability of gene expression loop mathematically using a parameter set mentioned in “method” paragraph in Chapter 1. We conducted this analysis referring to these papers including similar analysis.
- Tanaka, G., Tsuji, S., & Aihara, K. (2009). Grazing-induced crises in hybrid dynamical systems. Physics Letters A, 373(35), 3134-3139.
- Tanaka, G., Tsumoto, K., Tsuji, S., & Aihara, K. (2008). Bifurcation analysis on a hybrid systems model of intermittent hormonal therapy for prostate cancer. Physica D: Nonlinear Phenomena, 237(20), 2616-2627.
We excluded the fluorescent proteins and mRNA encoding them from this analysis, because they do not affect the stability of the expression loop of sigma factor and anti-sigma factors. Arabinose whose concentration declines over time is also excluded. For, if arabinose is included into vector X, there become no fixed points. Vector X and fixed points are mentioned below paragraphs.
We put concentration of sigma-factor A, B, C, anti-sigma factor A, B, C, mRNA encoding sigma-factor A, B, C (without toehold switch), mRNA encoding sigma-factor A, B, C (with toehold switch), mRNA encoding anti-sigma factor A, B, C as x1, x2, ...., x16, respectively. And we defined vector X = (x1, x2, …, x16). This vector X represents a state of a cell. If X represents a state of a cell which is at the start of cell cycle, the state of the cell three cell cycles later can be represented as P(X). P(X) is a function whose input is X. In other words, E. coli in X state changes into P(X) state after three cell division.
It is existence of X which satisfies two conditions simultaneously that stable establishment of expression loop requires. First one is $P(X) - X =0$ (condition A), and the second one is eigenvalues of Jacobian matrix of $P(X) - X$, or $\frac{\partial (P - X)}{\partial X}$(16*16 square matrix) are all negative (condition B). Condition A means the state of E. coli does not change after three generations and it is a necessary condition for gene expression loop of three generations. Xs satisfying condition A are called fixed points. While condition B means fluctuated states (concentration of each factor) from a fixed point will go back to the fixed point as time passed, it is a condition for the loop to maintain stably regardless of the initial state and fluctuation in E. coli. Therefore, the task of our developed tool is judging the existence of fixed point X satisfying both condition A and B.
The analysis tool first finds X satisfying condition A, subsequently check if the fixed point X satisfies condition B or not. The process of searching for X satisfying condition A is performed with an arranged algorithm “differential evolution”. In this aranged algorithm, cost function is norm of P(X)-X and the population are composed of candidates of X. P(X) is calculated by numerical integral, Euler method.
The process of judging condition B is done in this way. First, Jacobian matrix $\frac{\partial (P - X)}{\partial X}$ is calculated with numerical approximation. Second, eigenvalues of the Jacobian matrix are calculated with LU decomposition method. Then whether each eigenvalue is plus or minus is judged. For convenience’ sake, numerical integrals calculation are all performed ignoring Gaussian noise, delay of transcription and translation, and influence of arabinose. We wrote a code which implements this process with an inputted parameter set and return the result of stability judging. The code is below.
File:T--UT-Tokyo--Modeling--Stability.zip
Result and Discussion
The code above (Stability.java) judged that the expression loop is stable when we inputted a certain parameter set which made a positive result when simulated (Parameter Set A in the Section 4). This judgement mathematically supports our expectation that the genetic circuit generates stable expression loops under valid parameter sets. Now this code enables us to judge whether the circuit generates stable expression loops under various sets of parameters obtained from literature or experiment.
Parameters Fitting with the Results of Experiment
Aim
The tool explained in chapter 1 and 2 enabled us to examine in advance whether the gene expression loop would be stable with a parameter set of the expression, decomposition rates, etc. Therefore, we experimented with real E. coli strain, growth environment and other factors to find parameters which are suited to the simulation with the tool.
Method
We did two experiments. First one is putting GFP gene in downstream of Pnrd and measuring the time shift of fluorescent strength of GFP. Second one is putting GFP in downstream of Pconst and conduct the same measurement as above. The concentration of GFP estimated from fluorescent strength is shown in the table below. The data obtained from these experiments are shown below.
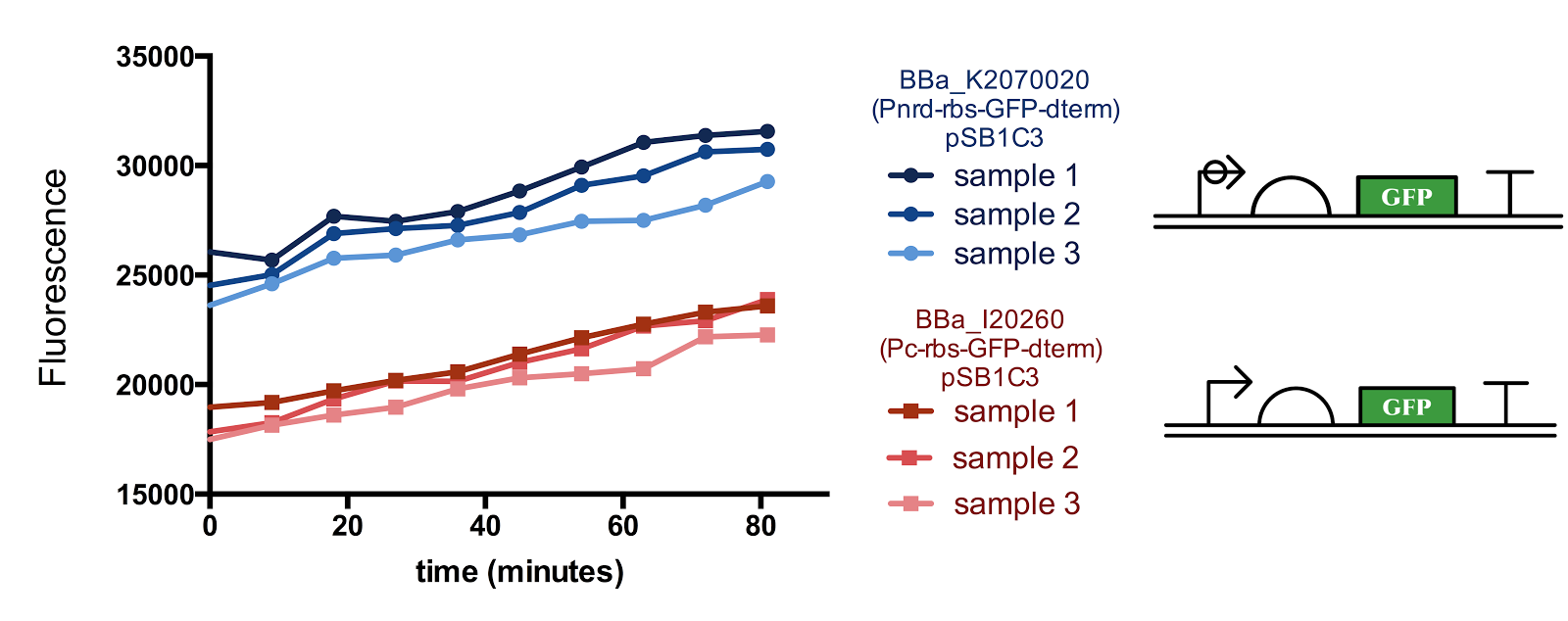We estimated the transcription rate of genes in downstream of Pnrd ($TC_{pnrd}$), transcription rate of genes in downstream of Pconst ($TC_{pconst}$), translation rate of protein (GFP) ($TL$), half-life of mRNA ($HL_{mRNA}$), half-life of GFP ($HL_{GFP}$), maturation time of GFP ($MT$), cell cycle ($CYCLE$) and length of activation period of Pnrd ($PNRD$), by parameter fitting.
In the experiment using Pnrd, the time series of concentration of mRNA encoding GFP, immature GFP protein, and mature GFP protein would be described by following differential equations. $$\frac{d[\mathrm{mRNA}]}{dt} = TC_{pnrd} - \frac{\ln{2}}{HL_{mRNA}} [\mathrm{mRNA}] \mathrm{(with Pnrd)} $$ $$\frac{d[\mathrm{mRNA}]}{dt} = - \frac{\ln{2}}{HL_{mRNA}} [\mathrm{mRNA}] \mathrm{(without Pnrd)} $$ $$\frac{d[\mathrm{imGFP}]}{dt} = TL [\mathrm{mRNA}] - [\mathrm{imGFP}] \frac{\ln{2}}{HL_{GFP}} - \frac{\ln{2}}{MT} [\mathrm{imGFP}] $$ $$\frac{d[\mathrm{GFP}]}{dt} = \frac{\ln{2}}{MT} [\mathrm{imGFP}] - \frac{\ln{2}}{HL_{GFP}} [\mathrm{GFP}] $$ In the experiment using Pconst, differential equations of mRNA would be described as follows. Differential equations of GFP proteins would be same as above. $$\frac{d[\mathrm{mRNA}]}{dt} = TC_{pconst} - \frac{\ln{2}}{HL_{mRNA}} [\mathrm{mRNA}]$$ We fitted measured value with these equations with an algorithm called “differential evolution”. We also developed a tool which can calculate parameters with inputted data and output the result. The source code of the tool is this.
File:T--UT-Tokyo--Modeling--Fitting.zip
Result and Discussion
We inputted the data from the experiments mentioned above into our parameter fitting tool, but unfortunately, meaningful output was not acquired. For, when inputted the same data for several times, outputted parameters were different every time.
We considered that the result of this parameter fitting did not converge to a valid parameter set simply because there were too many unknown parameters to estimate from the finite amount of data. If we had conducted more experiment and obtained more data, there was a likelihood that the result of this parameter fitting converged to a certain set of parameters.
Parameters Estimation from Literature
We referred to the table below to decide parameters. Each literature showed various values. For this reason, we referred just the order of the parameters.
| Parameter | value | reference |
| Transcription rate | 4200 nt/min | PKU igem 2009 |
| Transcription | 18.2 nM/min | Bielefeld 2015 (cell free) |
| 2700 nt/min | Manchester 2015 | |
| 2400-3300 nt/min | “Modulation of Chemical Composition and Other Parameters of the Cell by Growth Rate” | |
| Openwetware | ||
| Openwetware | ||
| 2-3nM/min | E.coli stats | |
| A forward-design approach to increase the production of poly-3-hydroxybutyrate in genetically engineered Escherichia coli | ||
| 3000 nt/sec | ||
| 4200nt/sec | ||
| 32nM/min(Transcription rate(6) in E.coli/ conc. of gene) | ||
| Translation rate | 2400Aa/min | PKU igem 2009 |
| Translation | 1200AA/min | Manchester 2015 |
| 720-1320AA/min | “Modulation of Chemical Composition and Other Parameters of the Cell by Growth Rate” | |
| Openwetware | ||
| openwetware | ||
| E.coli stats | ||
| 2-3nM/min | ||
| 1200 Aa/min | ||
| 2400 Aa/sec | ||
| Dissociation constant | 10^-7 to 10^-5 M( | A Model for Sigma Factor Competition in Bacterial Cells |
| (promoter-sigma) | ||
| Dissociation constant | 0.01nM ( | A Model for Sigma Factor Competition in Bacterial Cells |
| (sigma-anti sigma) | ||
| 50nM ( | ||
| mRNA degradation rate constant | 0.157/min | PKU igem 2009 |
| (ln2/half-life) | 0.139/min | NTU igem 2008 |
| 0.347/min | Manchester 2015 | |
| 0.347/min | Openwetware | |
| 0.66/min | Stochastic sequence-level model of coupled transcription and translation in prokaryotes | |
| Protein degradation rate constant | 0.0231/min (dilution rate due to cell division) | Openwetware |
| (ln2/half-life) | ||
| 0.102/min | Stochastic sequence-level model of coupled transcription and translation in prokaryotes | |
| Leuven 2013 | ||
| A forward-design approach to increase the production of poly-3-hydroxybutyrate in genetically engineered Escherichia coli | ||
| 10h or 2 min (0.00116/min or 0.246/min) | ||
| 0.035/min(Rate = ln2/doubling time) | ||
| Protein with degradation tag degradation rate constant | 40-370 min (0.0173/min - 0.00187/min) | Edinburgh 2014 |
| (ln2/half-life) | ||
| Generation time | 120min | Escherichia coli Ribonucleotide Reductase Expression is Cell Cycle Regulated |
| “Cell division” time | 15 min | Escherichia coli Ribonucleotide Reductase Expression is Cell Cycle Regulated |
In addition, we referred to this paper to know parameters related to sigma factors or anti-sigma factors.
- Rhodius, V. A., Segall‐Shapiro, T. H., Sharon, B. D., Ghodasara, A., Orlova, E., Tabakh, H., ... & Voigt, C. A. (2013). Design of orthogonal genetic switches based on a crosstalk map of σs, anti‐σs, and promoters. Molecular systems biology, 9(1), 702.
The instances of the parameter sets that we mentioned in the Section 1 and 2 are as follows. The unit of concentration is μM, and the unit of time is h.
Parameter Set
| Parameter | Set A | Set B |
| $$k$$ |
1800 | 1800 |
| $$\alpha$$ |
120 | 120 |
| $$C_{low}$$ |
0.01 | 0.01 |
| $$C_{high}$$ |
0.1 | 0.10 |
| $$K_a$$ |
1 | 1 |
| $$K_b$$ |
1 | 1 |
| $$K_c$$ |
1 | 1 |
| $$K_{araC}$$ |
0.01 | 0.01 |
| $$K’_a$$ |
1 | 1 |
| $$K’_b$$ |
1 | 1 |
| $$K’_c$$ |
1 | 1 |
| $$K’_{araC}$$ |
0.01 | 0.010 |
| $$K’’$$ |
1 | 10 |
| $$c_{araC}$$ |
100 | 100 |
| $$HL_{\sigma A}$$ |
0.15 | 0.15 |
| $$HL_{\sigma B}$$ |
0.15 | 0.15 |
| $$HL_{\sigma C}$$ |
0.15 | 0.15 |
| $$HL_{\sigma -A}$$ |
0.15 | 0.15 |
| $$HL_{\sigma -B}$$ |
0.15 | 0.15 |
| $$HL_{\sigma -C}$$ |
0.15 | 0.15 |
| $$HL_{RNA}$$ |
0.05 | 0.05 |
| $$HL_{arabinose}$$ |
0.5 | 0.5 |
| $$HL_{GFP}$$ |
0.25 | 0.25 |
| $$HL_{RFP}$$ |
0.25 | 0.25 |
| $$HL_{CFP}$$ |
0.25 | 0.25 |
| $$MT_{GFP}$$ |
0.2 | 0.2 |
| $$MT_{RFP}$$ |
0.2 | 0.2 |
| $$MT_{CFP}$$ |
0.2 | 0.2 |
