Introduction
One of the goals of our project is to visualize if the system we designed to bring DNA strands closer works. We decided to use a tripartite GFP for that purpose. As we explained on our Strategy page, this system is composed of several parts:
- The two dCas9 proteins
- The two linkers
- The three parts of the GFP
To visualize the fluorescence, the tripartite GFP needs to assemble. The 10th and 11th β-sheets of the GFP will be linked to the dCas9 and the GFP’s β-sheets from 1 to 9 will be free in the bacteria. We wanted to design our system to be sure that the GFP tri-partite assembles. To do that, we needed to find the optimal distance between the two target sequences that results in fluorescence.
Constraints and Limits
The first constraint for the distance is the following: if the distance between the two dCas9 is too far, the tri-partite GFP may never assemble, as illustrated below.
On the other hand, when the end-to-end distance of the linker is too short, steric hindrance impedes upon the assembling of the GFP-tripartite. The two dCas9 proteins are not in the same plan and the DNA must curve. This affects the distance between the target sequences because curved DNA is longer than straight DNA. Illustration below:
Before using this system, we needed to answer a very essential question: what is the optimal distance between the two dCas9 proteins required for GFP to fluoresce?
In our model, we can liken the distance between the target sequences to the distance of the two dCas9 proteins, since each sequence is lodged in the core of each dCas9 protein. This allows us to calculate the distance between the two dCas9 proteins based on the distance between the target sequences.
To design the different target sequences, we converted the distance d between the two dCas9 proteins (in Angstrom) into the distance bp on the DNA (in base pair). To obtain the distance in base pairs, we need the length of a helix turn, which is 34Å, and the number of nucleic acids in a helix turn, which is 10.5 nucleic acids. This gives us the number of base pairs:
bp = (d * 10.5)/34
Our conversion relies on several hypotheses: we considered the DNA as a linear B-DNA, and we neglected the structural modification of the DNA due to the fixation of the two dCas9.
It appeared that the calculating power of a computer would be more than welcome to estimate the optimal distance through simulation.
Models implemented
3D Model
We first thought of building a simple 3D model using the proteins’ known structures. We found these structures on the RCSB Protein Data Bank and used Pymol to assemble the system.
For this model we used:
- Two identical dCas9 proteins from Streptococcus Pyogenese (instead of Streptococcus Thermophiles and Neisseria Meningitidus in our biological system)
- A wild type GFP where we removed the 10th and 11th β sheets to mimic the tripartite GFP.
The big limitation of this approach was the lack of information regarding the linker. We could not find any information concerning its 3D configuration apart from its sequence. Hence, we decided to use the PEP-FOLD software to build a 3D simulation. However, the predictions we obtained seemed very unlikely to appear naturally. Indeed, the linker is supposed to be 100% unfolded because its sequence includes a majority of glycine, whereas some of the PEP-FOLD results showed β-sheets in the linker’s structure, as illustrated underneath:
A representative PEP-FOLD prediction of the linker
PEP-FOLD, a software designed for the prediction of the structural configuration of folded proteins, gives predictions biased towards folded structures due to its innate optimization algorithm. As such, the configurations we obtained for our linker, conceived to be unfolded, are most likely invalid.
So we decided to build two extreme models to try to flank the exact value: one with a small end-to-end distance and another one with a long distance.
For the small end-to-end distance, we used one of the PEP-FOLD conformations because even if the configuration seemed unlikely, the protein is maximally folded. As such, the smallest end-to-end distance we found with the PEP-FOLD predictions was 16.4 Å.
For the long end-to-end distance, we used the linker without any spatial folding, hence in a linear conformation. Similarly, this spatial configuration is very improbable too, but provides us with the maximal theoretical bound on the end-to-end distance. We obtained 107.3 Å.
With the preceding linker configurations, we then used the Pymol software to design the 3D model of the entire system and find the distance between the target sequences, lodged in the dCas9 attached to the GFP through the linker, in each case. According to the equation of conversion above, we acquire a first range of values for the optimal distance between the two target sequences:
- For the smallest linker, we found a distance of 230Å which corresponds to 71 base pairs
- For the longest linker, we found a distance of 356Å which corresponds to 110 base pairs
The limit of this approach is the way we modeled the linker, the distance between the target sequences depending on it. Hence, we decided to approximate the linker’s end-to-end distance through a mathematical equation which describes polymer physics and will provide an estimation of the end-to-end distance of the linker.
Ideal Chain an Worm-Like Chain Models
We used two polymer physics models to approximate the linker end-to-end distance: the Ideal Chain model and the Worm like Chain model.
The Ideal Chain model (or freely jointed chain) is a simple model to describe polymers. It models a polymer with the help of a random walk, a mathematical object that assumes the construction of the object results from a succession of random steps. In this model, each amino acid in our linker will be considered as a rigid rod with a fixed length and modeled as a segment. We also consider that each amino acid is independent concerning its orientation and its position with its neighbor.
Thus, we have 36 segments, and the length of each segment is 3.7Å.
For N segments with a length of l, the contour length L is the total unfolded length:
R is the end-to-end vector, and its mean value writes:
According to the central limit theorem, if N>30, the probability density PN (r ⃗) for the end-to-end distance in the Ideal Chain takes the following Gaussian form:
Now that we have the Ideal Chain model equation governing the corresponding end-to-end distance, we will elaborate upon the Worm-Like Chain model which will serve as comparison to the results obtained with the Ideal Chain model.
In contrast with the Ideal Chain model, which considers the flexibility of segments in a discrete way, the Worm-Like Chain model considers the flexibility continuously, which is suited for describing semi-flexible polymers. Since we did not have any information concerning the flexibility of our linker, we decided to study both models to cover both cases and maximize the amount of information at our disposal concerning possible end-to-end distances according to flexibility.
The Worm-Like Chain model uses the persistence length, which quantifies the stiffness of a polymer, in the calculation of the end-to-end distance.
For our linker, we adopted the persistence length value used in the paper Huan-Xiang Zhou (2004): Polymer Models of Protein Stability, Folding, and Interactions, where the probability function is defined as follow:
With the equations determining the linker’s end-to-end distance from each model, we wrote a Python program that shows the density of probability distributions of the end-to-end distance in each case. The resulting graph is displayed below:
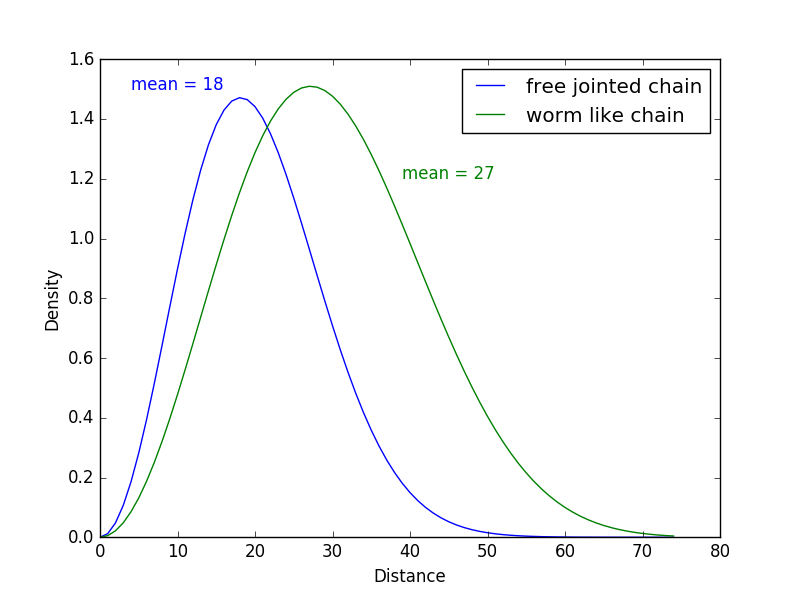
End-to-end distance density of probability according to the model used
We see on this graph the distances predicted by the two models, with a mean of 18Å for the Ideal Chain model (in blue) and a mean of 27Å for the Worm-Like Chain model. The difference in the end-to-end distance between the two models is coherent because the Worm-Like Chain model is suited for stiffer polymers that are longer and less folded up than the polymers described with the Ideal Chain model.
These results are interesting because we can see that the end-to-end distance results we obtained with the PEP-FOLD prediction and with the mathematical models are quite similar.
These models help us adjust the distance we need for the linker. Indeed, we can assume that the end-to-end distance is closer to 20Å than 100Å. However, we cannot conclude anything yet and we cannot develop our model further because we do not have enough information about the stiffness of our linker.
The biggest limitation of these models is the fact that we lose information regarding the spatial arrangement of the repeat units and we do not have any information concerning the steric hindrance the repeat units would eventually apply upon each other.
If we consider our real polymer chain, the rotation of bonds around the backbone is restricted due to hindered internal rotations and excluded-volume effects. With this consideration, we know that our results are biased.
The ideal and worm-like chain models gave us the order of magnitude of the expected results, but we need to adapt our model to account for steric hindrance, so we decided to develop our own model to describe the behavior of the linker.
Our mathematical model
Definitions
We wanted our model to provide the end-to-end distance, as well as simulate the linker in 3D.
We use this scheme: all bonds have the same length, the angle θ represents the angle between two atoms, and Φ, Ψ, ω, are the dihedral angles.
Unlike the mathematical models, in this model each segment is a bond rather than an amino acid. We thus have 36*3=108 segments.
To simulate our linker in 3D, we decided to write a program, where we represented each segment by a vector and then added these vectors in the same base. The sum of the segment vectors 0 to i is called Ui. In the end, we obtain one vector U107 that represents the end-to-end vector. We also keep the coordinates along the way so as to end up with a 3D representation of our linker.
This program was written in Python because this language is suited for biological modeling and the 3D library was suited for the construction of our linker.
Thanks to the Pymol software and the literature [1], we know the following constants:
- The length l of each segment : 1.5 Å
- The angle θ which represents the angle between each atom in the amino acid : 2π/3
We also use the Ramachandran plot to determine the appropriate dihedral angles Φ and Ψ.
The figure below describes how we constructed our model in 3D.
For each segment of our model, we can be in any one of the three following situations (see the scheme below):
To do that, we initialize the first vector on the Oz axis and then all the others segments will be expressed in that vector-base.
For each segment of our model we have three possibilities:
- The liaison N-Cα with the Φ angle
- The liaison Cα-C with the Ψ angle
- The liaison C-N which is the peptide bond
We have to define a change of basis matrix and consider the first two liaisons. For the peptide bond, we only consider the Rx matrix because Φ = 0.
We define an initial vector:
And we construct the change of basis matrix with a translation matrix Tz, a rotation matrix on the Oz axis Rz, and a rotation matrix on the Ox axis Rx:
- Tz represent the translation of 1.5 Å corresponding of the segment length
- Rz represent the Φ or Ψ rotation
- Rx represent the θ rotation with a fix θ angle. It is define relatively with the Ox axis and that lead to a rotation of the coordinate system on the Ox axis.
Then we have the change of base matrix: P = Tz * Rz * Rx. With this matrix, we can pass the vector n in the base of the vector n-1.
To each new segment, we define a value for Φ (that depends on the liaison of the amino acid). And we calculate for each Ui segment:
In the last step, we conserve the coordinates of each vector for plotting the 3D visualization.
We complete our model by adding parts. We consider that our linker is not entirely consisting by glycine and we add a test for adjusting dihedral angles because other amino acids don’t share the same Ramachandran plot.
We also define an exclusion zone for each vectors. With this, we exclude non biological covering.
Results
Our program is design to give the end to end distance on n simulations, to give a study of the RMSD and to show one simulation of the linker in 3D.
For 5000 simulations we obtain this graph:
As we can see the mean of end to end distance is 19.66 and the standard deviation is 7.82. We can compare our results to the other we obtain with the freely jointed chain.
When we study the distance and the repartition of the last segment we obtain:
In the end, we want a 3D representation of our linker and we obtain:
With our program we can obtain more information and have an idea of how our linker look on 3D and the space it can fold.
Gromacs software
On this graph, we print the end to end distance to see the dynamic obtained with Gromacs.
The results are:
- Protein Average end to end distance: 2.223 (nm)
- Average radius of gyration: 0.934 (nm)
This results are really close to our program results.
With these results, we can say that our program give good results for the prediction of unfolded protein.
We also obtain the graphs of RMSD and RMSF from Gromacs to have more information about the dynamic of our linker.
With these information, we can construct the 3D model of our system.
With Pymol software, we calculate the distance between the dCas9: 244.7 Å
Discussion and Limits
We can compare the results we obtained with our program and the results we obtained with other models. The freely jointed chain is the model that gives the better results for the end to end approximation. The worm like chain model is maybe not suitable for our kind of protein.
The Gromcas results show us that our program give a good estimation of the end to end distance and of the steric hindrance. We can also say that our program is running in less than 5 minutes while Gromacs program run in more than 8 hours.
Our model can be improve because we only see our linker at one time without the all dynamics.
In another way our program give a good estimation of the end to end distance and of the 3D conformation for unfolded protein. We never consider the folding like alpha helix or beta sheet because the results of the disorder of our linker was near to 100% so the program don’t consider these.