Modeling
We developed a MATLAB simulation in order to model how the system and concentrations would change through time. It takes into account the transcription and translation rates for our two enzymes, and the corresponding reactions that transform cysteine into hypotaurine. This simulation uses the parts and compositors MATLAB framework developed at MIT for the “Principles of Synthetic Biology” edX course.
The equations used to describe all reactions are based on the law of mass action, using estimated rate constants. The two enzymatic reactions would be better modeled with Michaelis-Menten equations, but we could not find characterization information for our two specific enzymes, and therefore the simpler mass action equation was used with a single rate constant. However, the code includes comments for changing this easily.


This model can be seen as a template which describes how the system would work in general, and can easily be edited to improve it with Michaelis-Menten kinetics if the enzymes are characterized to get a more accurate representation.
Below is a plot of how the system would behave with an initial cysteine concentration of 1000 nM. The CDO and CSAD lines overlap, as we assumed they are translated and degraded at the same rate.

As we can see in the plot, in this simulation the enzyme concentration increases until it stabilizes at 90.9 nM, and there is no change in the cysteine concentration until CDO and CSAD have been produced. After cysteine sulfinic acid starts being produced from cysteine, it immediately reacts with CSAD to form hypotaurine.
With no initial cysteine:
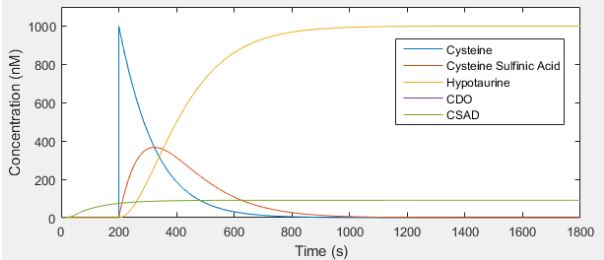
In this second plot we can see that if no cysteine is present, then no reactions take place. As soon as cysteine is added, the reactions start immediately as the enzymes were already produced.
We did not include them in the plots, but the simulation also takes into account the DNA, mRNA, and RNA polymerase concentrations in order to model the transcription and translation of the two enzymes.
Code:
%Fetches the framework
urlwrite('http://web.mit.edu/20.305/www/part_composition_setup.m', ...
'part_composition_setup.m');
rehash;
part_composition_setup('v5');
%Defines the system
sys = BioSystem();
%Concentration units are in nM and time in s
%Defines Constants
sys.AddConstant(Const('k_polf', 10)); %Polymerase binding
sys.AddConstant(Const('k_polr', 1));
sys.AddConstant(Const('k_trn', 0.1)); %Transcription
sys.AddConstant(Const('k_tln', 0.1)); %Translation
sys.AddConstant(Const('k_mdeg', 0.1)); % mRNA degradation & dilution
sys.AddConstant(Const('k_pdeg', 0.01)); % Protein degradation & dilution
sys.AddConstant(Const('k_1', 0.0001)); % Enzymatic reactions for hypotaurine
sys.AddConstant(Const('k_2', 0.0001));
%sys.AddConstant(Const('km_1', 0)); %Michaelis Menten constants
%sys.AddConstant(Const('km_2', 0));
%sys.AddConstant(Const('vmax_1', 0));
%sys.AddConstant(Const('vmax_2', 0));
%Defines Compositors
dcysdt = sys.AddCompositor('CYS', 0); % Cysteine
dCDOdt = sys.AddCompositor('CDO', 0); % Cysteine Dioxigenase
dCSADdt = sys.AddCompositor('CSAD', 0); % Cysteine Sulfinate Decarboxylase
dcsadt = sys.AddCompositor('CSA', 0); % Cysteine Sulfinic Acid
dhtdt = sys.AddCompositor('HT', 0); % Hypotaurine
dRNAPdt = sys.AddCompositor('RNAP', 1); % RNA Polymerase
dDNAdt = sys.AddCompositor('DNA', 1); % Promoter
dDNARNAPdt = sys.AddCompositor('DNARNAP', 0); % Promoter/RNApol complex
dmRNAdt = sys.AddCompositor('MRNA', 0); % mRNA
%Defines Parts
Hypot = Part('Prom -> Proteins -> Hypotaurine', [dDNAdt dRNAPdt dDNARNAPdt dmRNAdt dCDOdt dCSADdt ...
dcsadt dhtdt dcysdt], ...
[Rate('-k_polf * DNA * RNAP + k_polr * DNARNAP + k_trn * DNARNAP'), ... % dDNA/dt
Rate('-k_polf * DNA * RNAP + k_polr * DNARNAP + k_trn * DNARNAP'), ... % dRNAP/dt
Rate('k_polf * DNA * RNAP - k_polr * DNARNAP - k_trn * MRNA * DNA * RNAP'), ... % dDNARNAP/dt
Rate('k_trn * DNARNAP - k_mdeg * MRNA'), ... % dmRNA/dt
Rate('k_tln * MRNA - k_pdeg * CDO'), ... % dCDO/dt
Rate('k_tln * MRNA - k_pdeg * CSAD'), ... % dCSAD/dt
Rate('k_1 * CDO * CYS - k_2 * CSA * CSAD'), ... % dcsa/dt
Rate('k_2 * CSA * CSAD'), ... % dht/dt
Rate('- k_1 * CDO * CYS')]); %dcys/dt
%Michaelis-Menten Equations
%Rate('(vmax_1 * CYS) / (km_1 + CYS) - (vmax_2 * CSA) / (km_2 + CSA)'), ... % dcsa/dt
%Rate('(vmax_2 * CSA) / (km_2 + CSA)'), ... % dht/dt
%Rate('-(vmax_1 * CSA) / (km_1 + CSA)')]); % dcys/dt
sys.AddPart(Hypot);
%Solves/simulates the system
[T, Y] = sys.run_pulses([...
Pulse(0, 'CYS', 1000), ... % Initial conditions
%Pulse(200, 'CYS', 1000), ... % Add more cysteine at time 200
Pulse(1800, '', 0), ... % Stop at time 1800
]);
%Plot concentrations
figure();
plot(T, Y(:, sys.CompositorIndex('CYS')), ...
T, Y(:, sys.CompositorIndex('CSA')), ...
T, Y(:, sys.CompositorIndex('HT')), ...
T, Y(:, sys.CompositorIndex('CDO')), ...
T, Y(:, sys.CompositorIndex('CSAD')))
ylim([0 1100]);
legend('Cysteine', 'Cysteine Sulfinic Acid', 'Hypotaurine', 'CDO', 'CSAD')
xlabel('Time (s)');
ylabel('Concentration (nM)');
Look our funcTional model clicking here: https://static.igem.org/mediawiki/2016/7/72/T--BIOSINT_Mexico--Taurine_Production_Model.m
















