Team:SUSTech Shenzhen/Model/Simulation Force Field

Simulation of Microfludic Devices

FEM Analysis

Introduction

To make the analysis of experimental result is convincible, we also made the simulation using the Finite Element Method(FEM) to define that the field in microfluidic channel confirmed to our expectation.

FEM is a method for modeling and simulating physics-based problems. It divides a large problem into smaller elements, these smaller elements will be solved separately and then be assembled backed to the original model. A collection of smaller elements is called a “mesh”, the “mesh” is constructed by numerous elements, the smaller the size of the element is, the finer the “mesh” is, and the more accurate will the result be.

We made the simulation with the following procedures, and the result of maximum velocity and shear force applied on the bottom wall match with the mathematics perfectly.

Procedure

a. Geometry

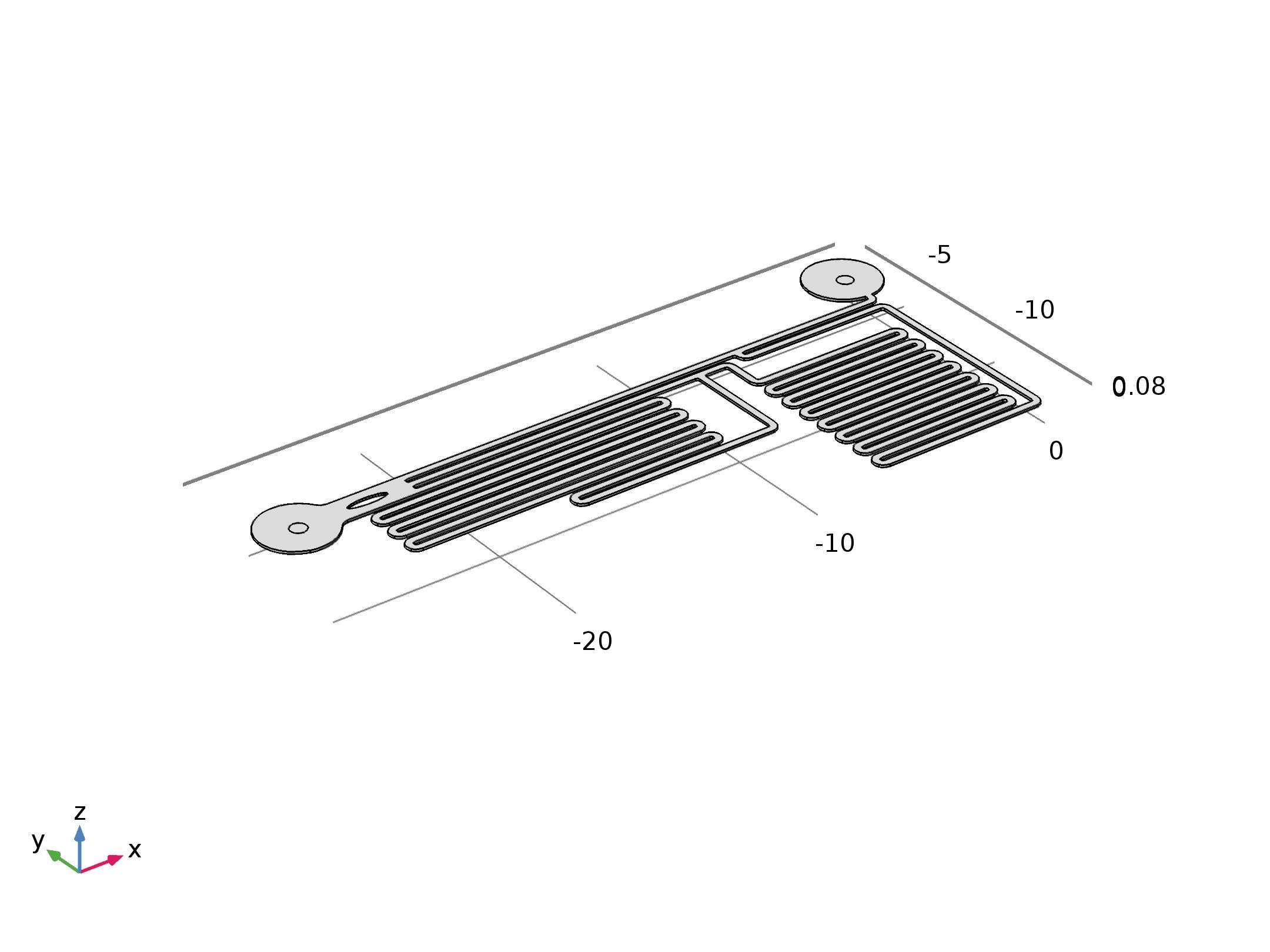
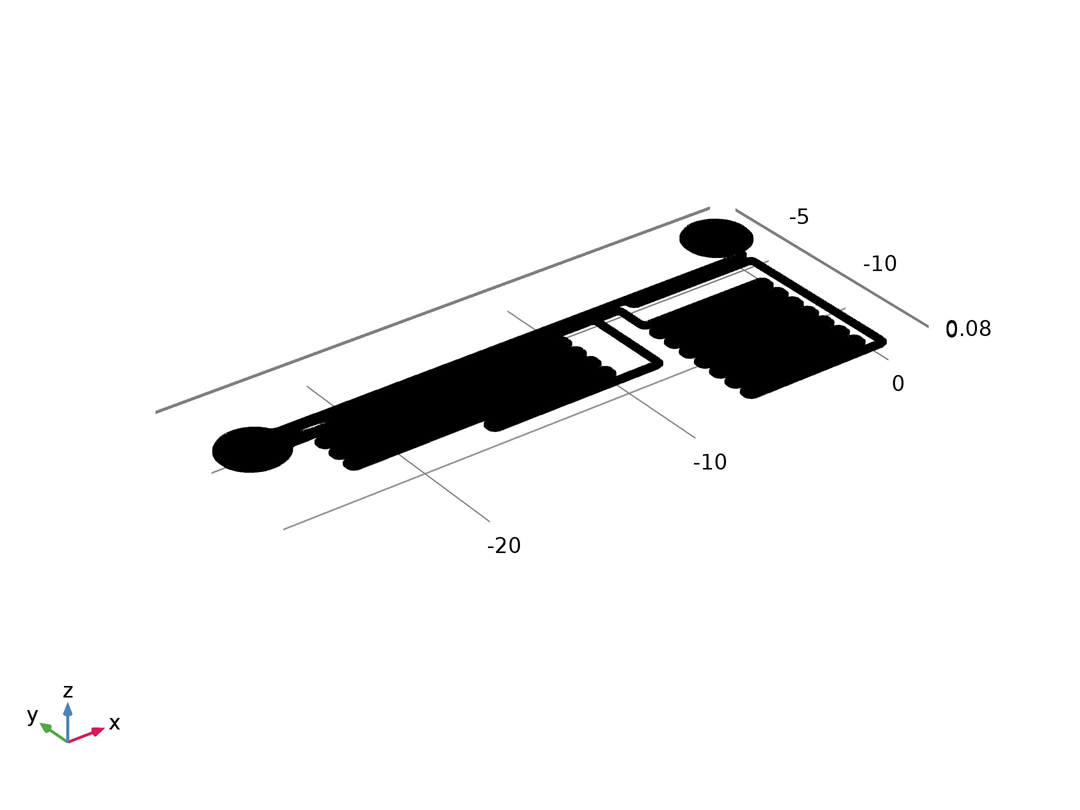
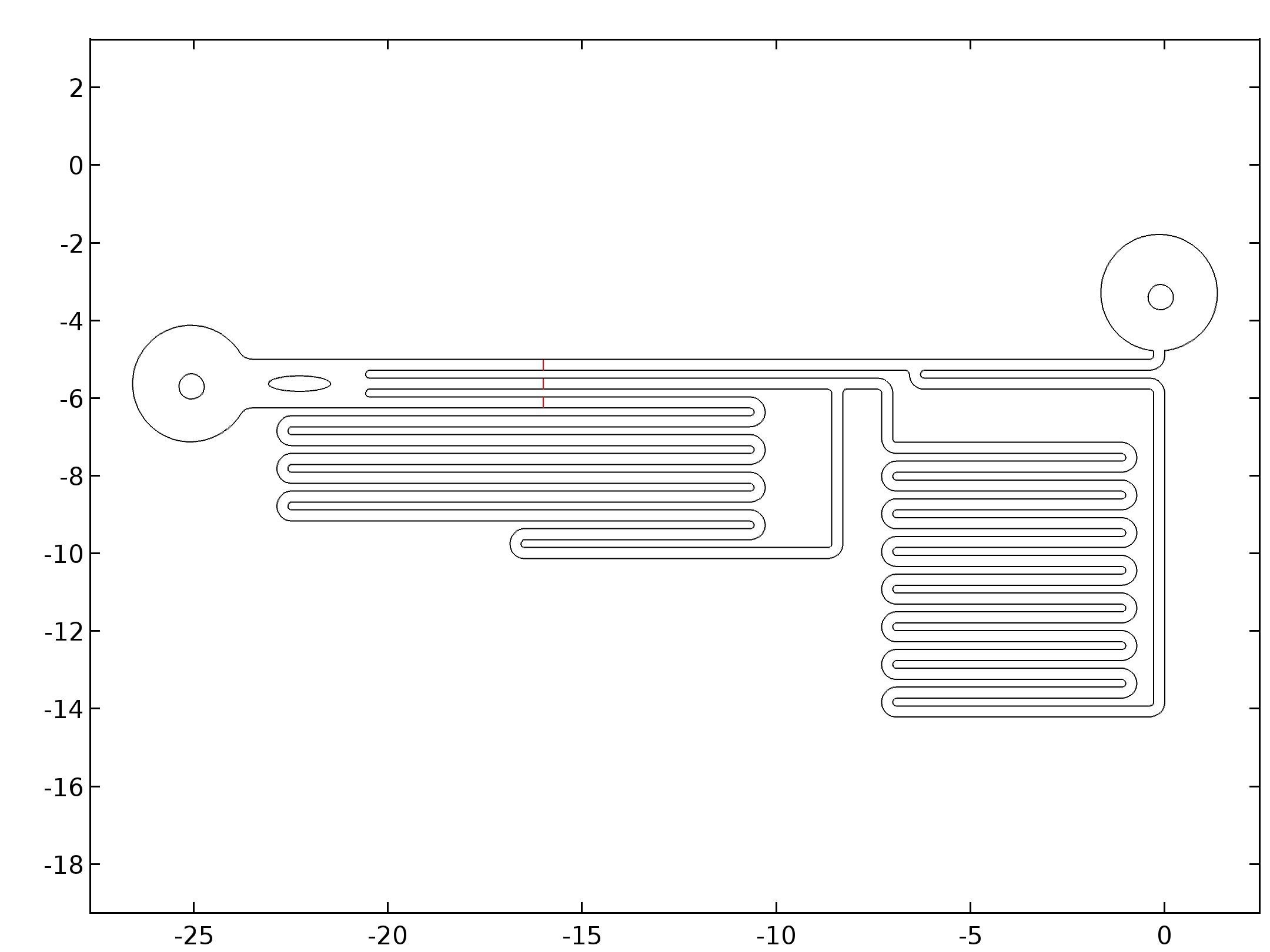
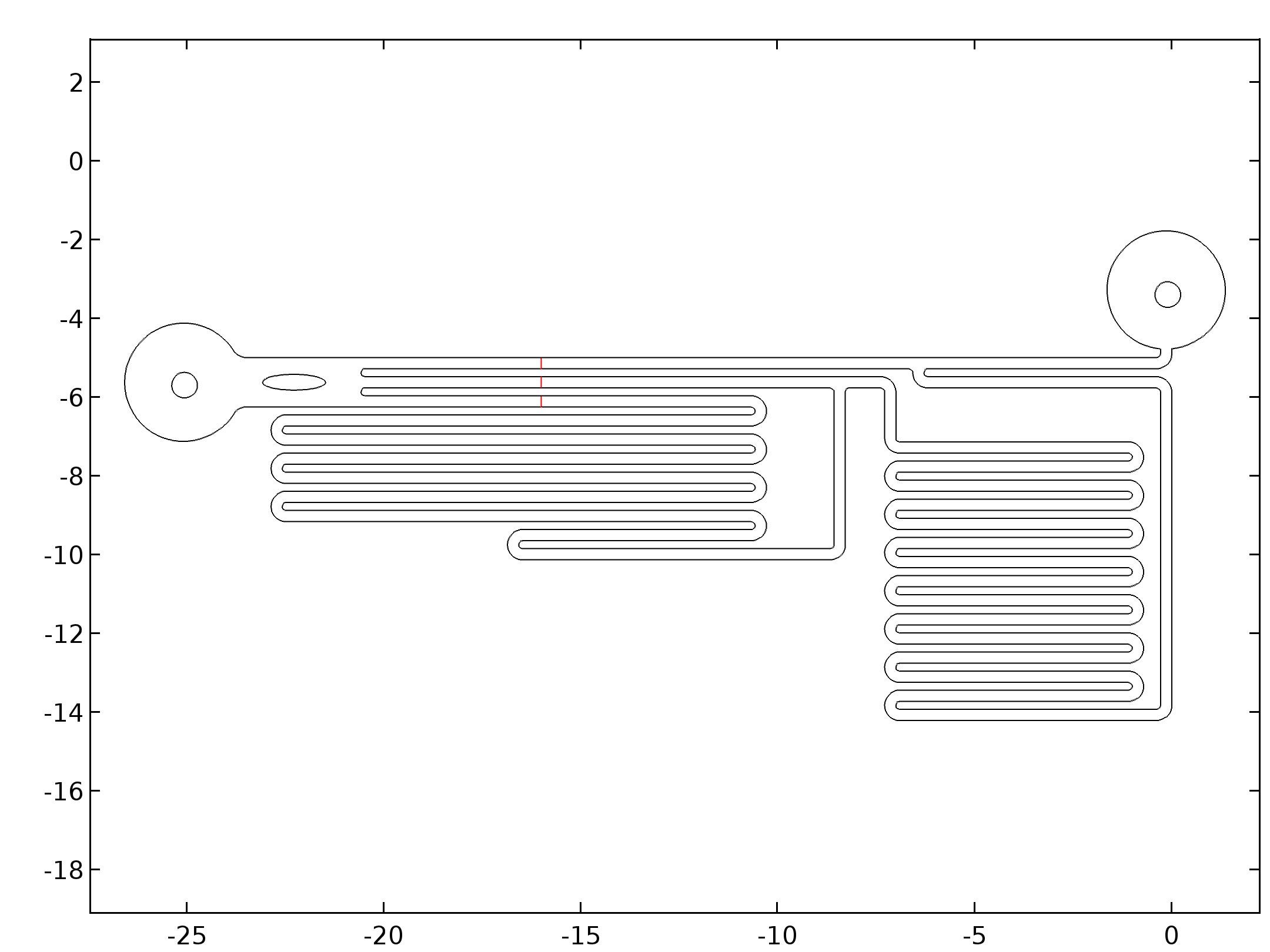
First we imported the designed CAD pattern file.

Then we draw two circles which have the diameter equal to the inner diameter of the fluid pipes that we used (0.65mm). The circles were placed around the center of the two circles we reserved for the fluid pipes. Since we used our bear hands to control the position of the holes for the fluid pipes in chip fabrication, the circles were just placed around the center parts like real cases.

Then we extruded the pattern to 90μm, and deleted the undesired parts. The final geometry was shown below.

Fig. 1 Final Geometry Setup

b.Parameters

All geometry domains were applied with the build-in material "water" to represent the petro medium that we used in our experiment.

The material parameters can be seen from bellow.

Description	Value
Dynamic viscosity	eta(T[1/K])[Pa*s]
Ratio of specific heats	1.0
Electrical conductivity	{{5.5e-6[S/m], 0, 0}, {0, 5.5e-6[S/m], 0}, {0, 0, 5.5e-6[S/m]}}
Heat capacity at constant pressure	Cp(T[1/K])[J/(kg*K)]
Density	rho(T[1/K])[kg/m^3]
Thermal conductivity	{{k(T[1/K])[W/(m*K)], 0, 0}, {0, k(T[1/K])[W/(m*K)], 0}, {0, 0, k(T[1/K])[W/(m*K)]}}
Speed of sound	cs(T[1/K])[m/s]

Table 1 Material Properties of "water"

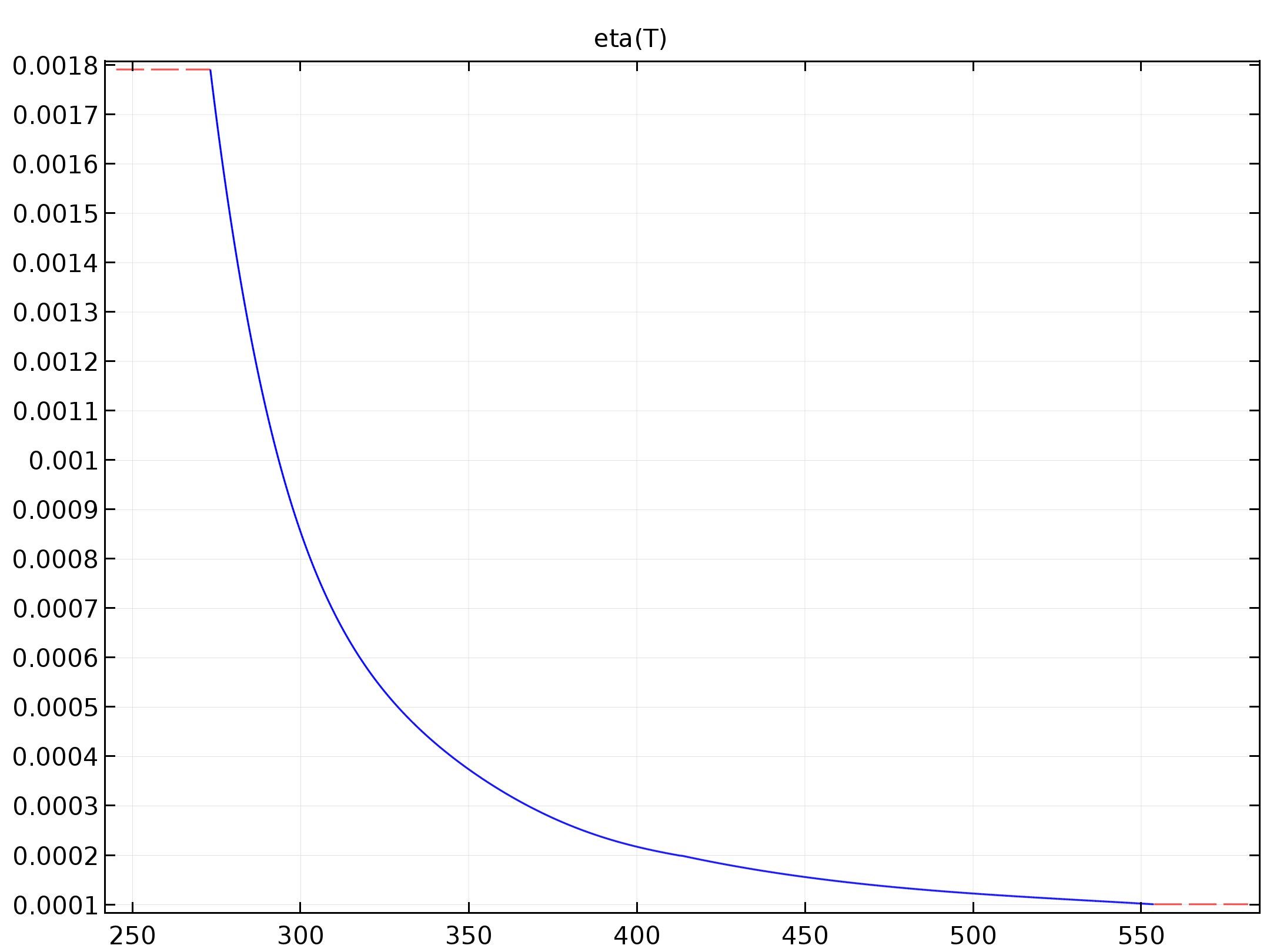
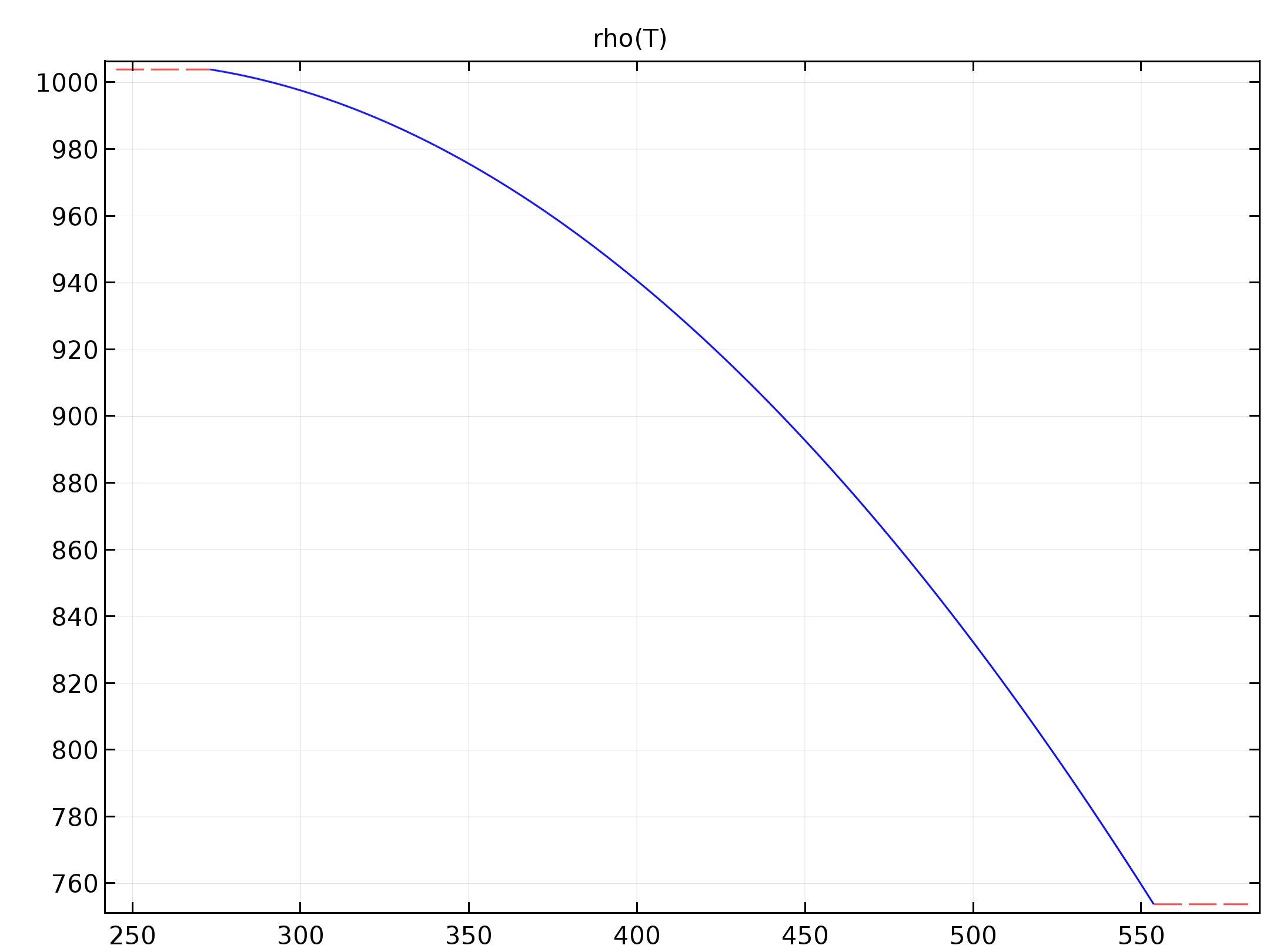
The parameters that we actually used was the dynamic viscosity (\eta(T)), and the density (\rho(T)). Their values with respect to the change of the temperature (K) can be seen form below.

\eta(T)=1.3799566804-0.021224019151*T^1+1.3604562827E-4*T^2-4.6454090319E-7*T^3+8.9042735735E-10*T^4-9.0790692686E-13*T^5+3.8457331488E-16*T^6 (273.15K\leq T\leq413.15K)

\eta(T)=0.00401235783-2.10746715E-5*T^1+3.85772275E-8*T^2-2.39730284E-11*T^3 (413.15 K\leq T \leq 553.75K)

rho(T)=838.466135+1.40050603*T^1-0.0030112376*T^2+3.71822313E-7*T^3 (273.15K\leq T \leq553.75K)

Fig. 3 Plot of \eta(T)

Fig. 2 Plot of rho(T)

Since the temperature of our model is set to the reference temperature as 293.15K, the respect value of \eta(T) and \rho(T) are 0.00101 Pa*s and 999.61509 kg/m³.

We used incompressible laminar flow interface to simulate our experiment, and the equations that the interface used is shown below.

\begin{matrix}\rho(\mathbf{u}\cdot \nabla)=\nabla \cdot [-p\mathbf I + \mu (\nabla \mathbf{u}+\nabla \mathbf{u^T})]+\mathbf{F} \\ \rho(\nabla)\cdot\mathbf{u}=0\end{matrix}

All boundaries except the inlet and the outlet circles were set to be no slipping walls.

Fig. 4 Boundaries Considered as "No Slipping Walls"

The inlet circle was given the velocity of 2.5113E-4 m/s, 7.534E-4 m/s and 0.0022602 m/s, which will give us the rate of flow values of 5μL/min, 15μL/min and 45μL/min.

The outlet circle was given the pressure of 0.

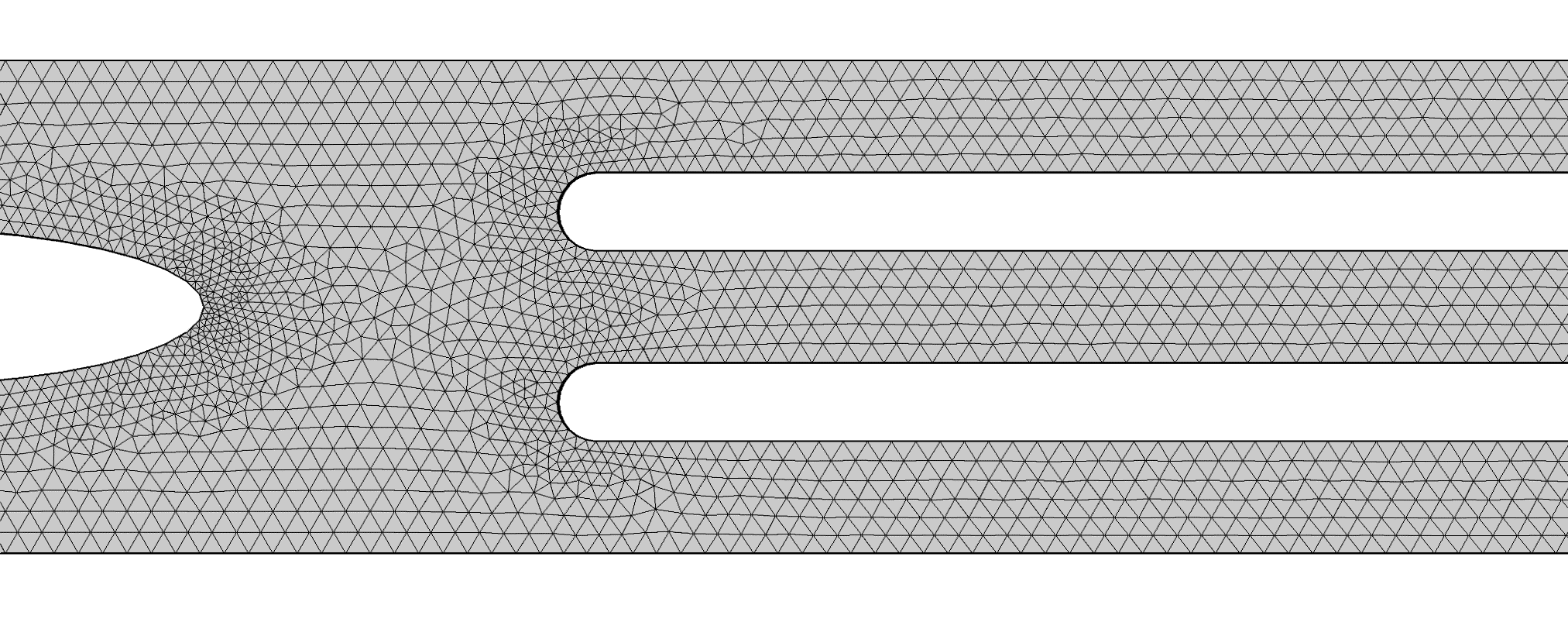
c. Mesh

Parameters of our mesh are shown below.

Description	Value
Minimum element quality	9.185E-4
Average element quality	0.4356
Tetrahedral elements	503702
Pyramid elements	260
Prism elements	363692
Triangular elements	182924
Quadrilateral elements	160
Edge elements	19326
Vertex elements	524

Table 2 Mesh Specifics

Fig. 5 Mesh Generated

By choosing this mesh size, the mesh generated was fine enough to give six solution points with in the width of a single channel.

Fig. 6 Mesh details

d. Solver Configuration

The solver was configured to compute for the stationary values under this specific model configuration. The relative tolerance was set to 0.000001, which means that the solver will only stop computing if the deviation of the result from the actual solution to the equations is under one in a million of the value of the actual solution.

e.Results

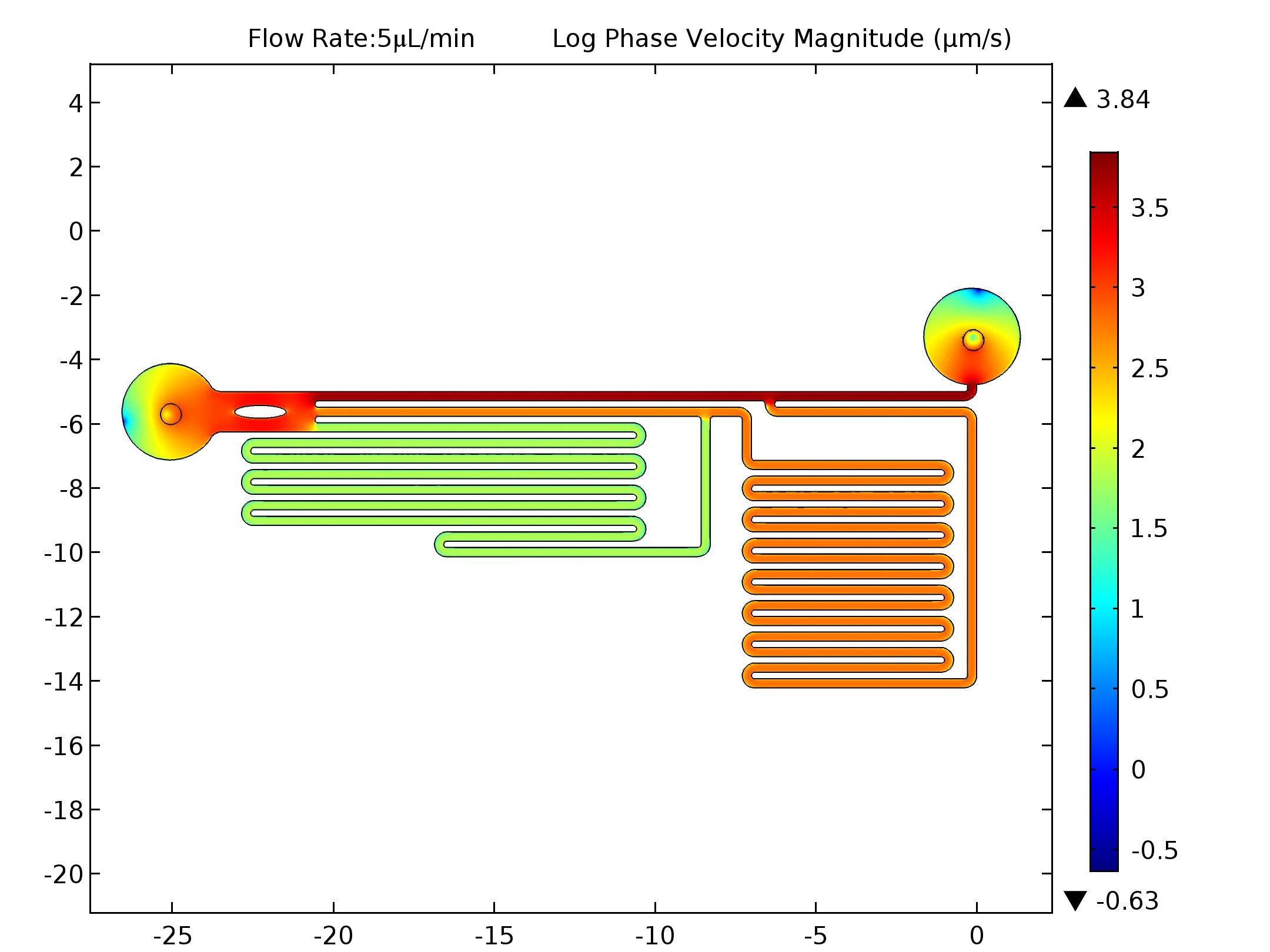
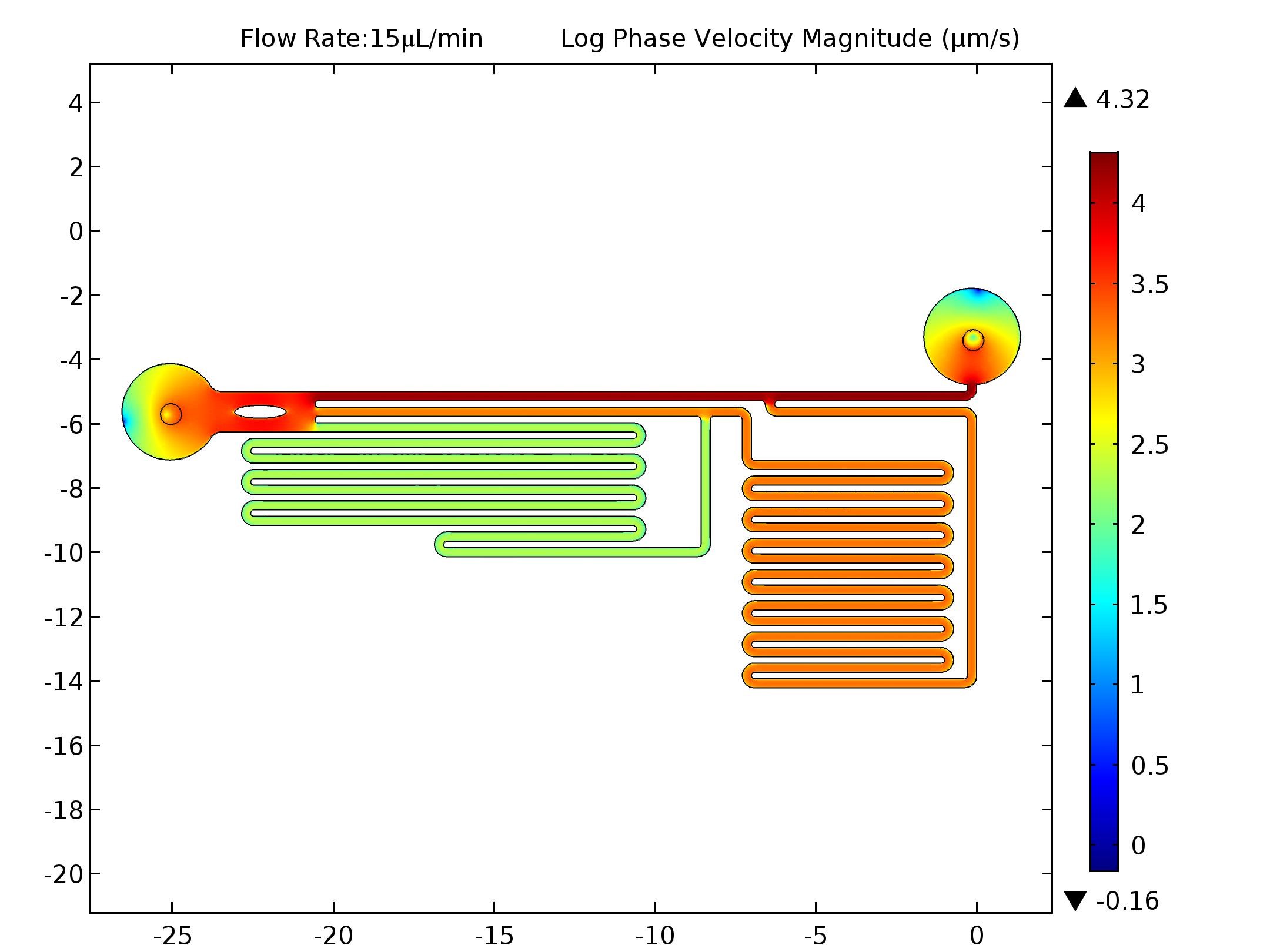
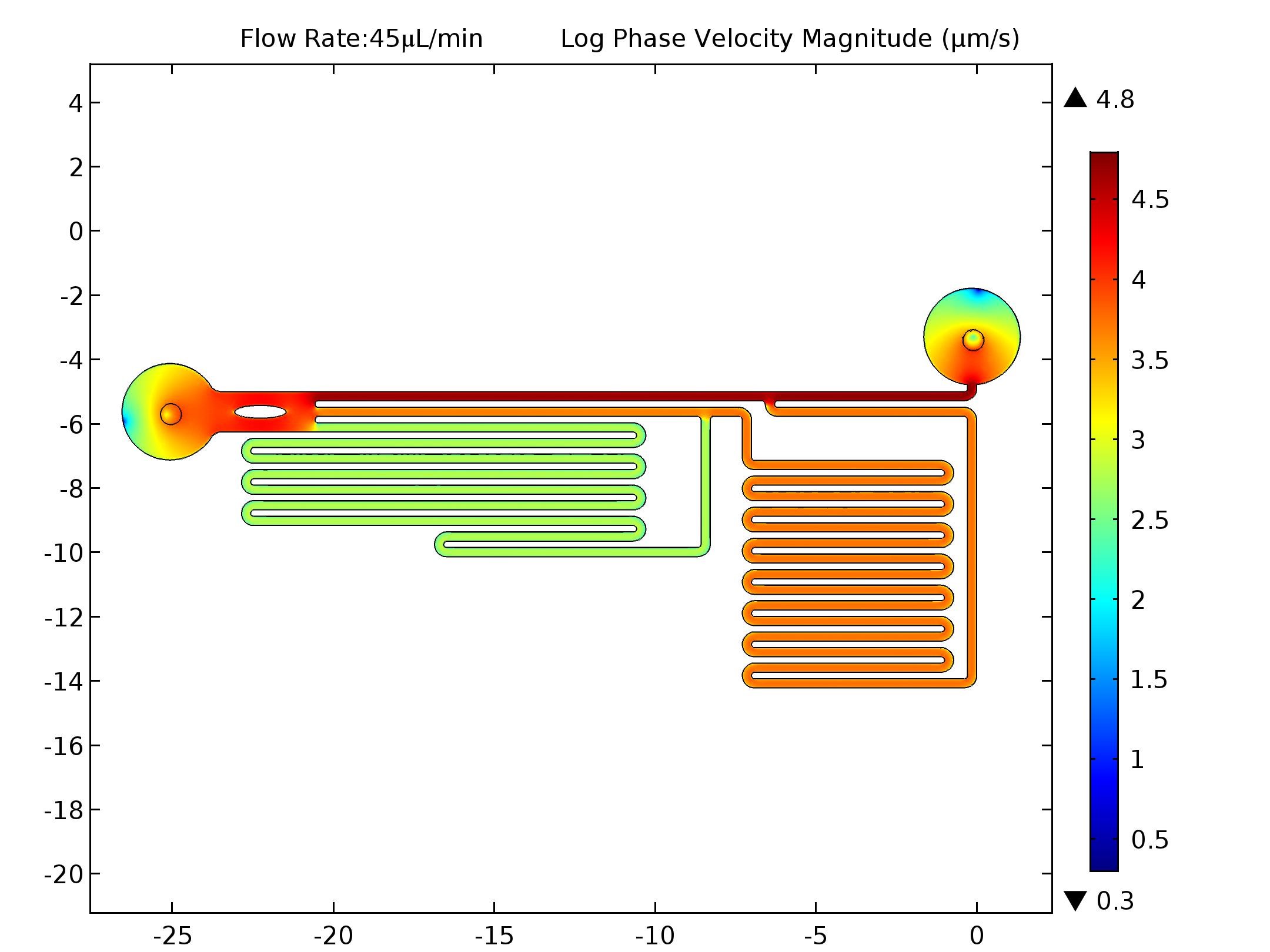
In the microfluidic channels the fluid will be applied a dragging force from the channel walls. So the fluid in the center line of the channel flows with the fastest speed.

In order to show the speed distribution inside the microfluidic channels, speed diagrams of the cut plane in the middle of the bottom plane and the top plane is shown below.

Fig.7 Velocity magnitude Distribution Under Input Flow Rate 5μL/min (log scale)

Fig.8 Velocity magnitude Distribution Under Input Flow Rate 15μL/min (log scale)

Fig.9 Velocity magnitude Distribution Under Input Flow Rate 45μL/min (log scale)

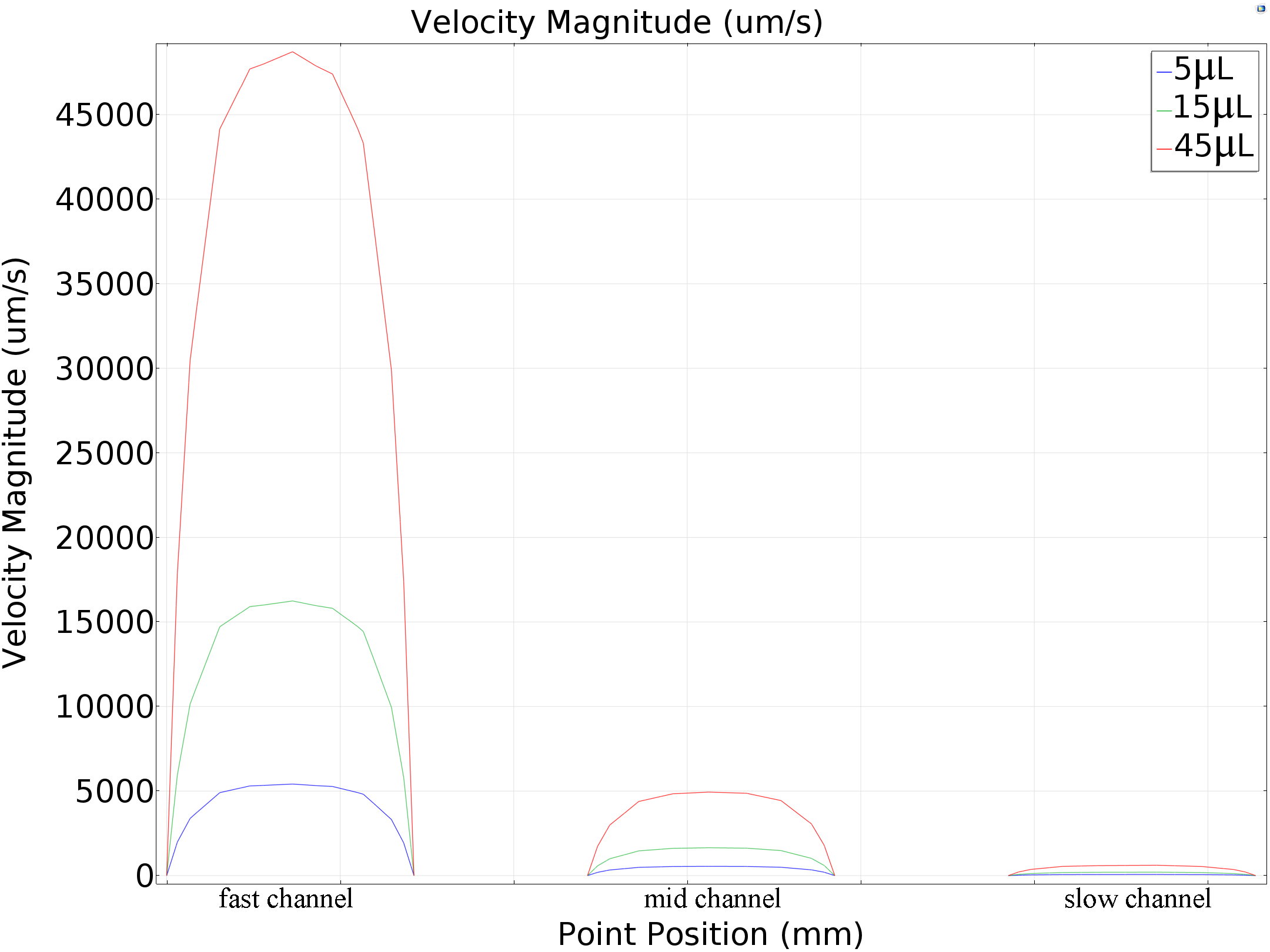
In order to further show the speed difference under three different parameters, we draw a line on the cut plane from (-16, -4) to (-16, -6.45) crossing through three microfluidic channels in the observation zone. and plot the flow speed on that line.

Fig.10 Cut Line Drawn

Fig.11 Velocity Magnitude Distribution on The Cut Line

The speed at the central line in all three channels at three different flow rate is listed below.

Channel Flow Rate	fast	middle	slow
5μL/min	5413.994μm/s	548.52153μm/s	67.9229μm/s
15μL/min	16241.73779μm/s	1645.63652μm/s	203.79536μm/s
45μL/min	48723.94763μm/s	4937.93255μm/s	611.65866μm/s

Table 3 Simulation Results of Central Line Speed

g. Discussion

In this simulation, we consider all the channel walls are rigid, but in real cases, channel walls will deform when pressure applied. So the cross section area of the channel will be larger than what we have considered in this simulation.

In real cases, the microfluidic channels have a lot of defects at the edges of the channels. So the dragging force applied by these channels will be larger than what we have considered in this simulation, causing the fluid to have a lower speed. But due to the random distribution of the defects, at some points, the defects might accelerate the fluid flow by making the channel to be narrower than usual.

Fig.13 Topside View of Microfluidic Channels 20X

Fig.12 Topside View of Microfluidic Channels 5X

In this simulation, microfluidic channel width was set to 285μm as we designed, with channel walls exactly perpendicular to the bottom. While as in real cases, due to the low transmittance of SU-8 photoresist to the low-wavelength light, the photoresist at the top side of the channel will absorb higher energy than the photoresist at the bottom, causing a trapezoidal cross section profile. The flow speed change caused by this phenomenon is still unknown to us.

Fig.15 Cross Section of Microfluidic Channels (SEM)

Fig.14 Cross Section of Microfluidic Channels (SEM)

Fig.17 Optical Transmittance of SU-8 Photoresist

Fig.16 Cross Section of Microfluidic Channels (SEM)

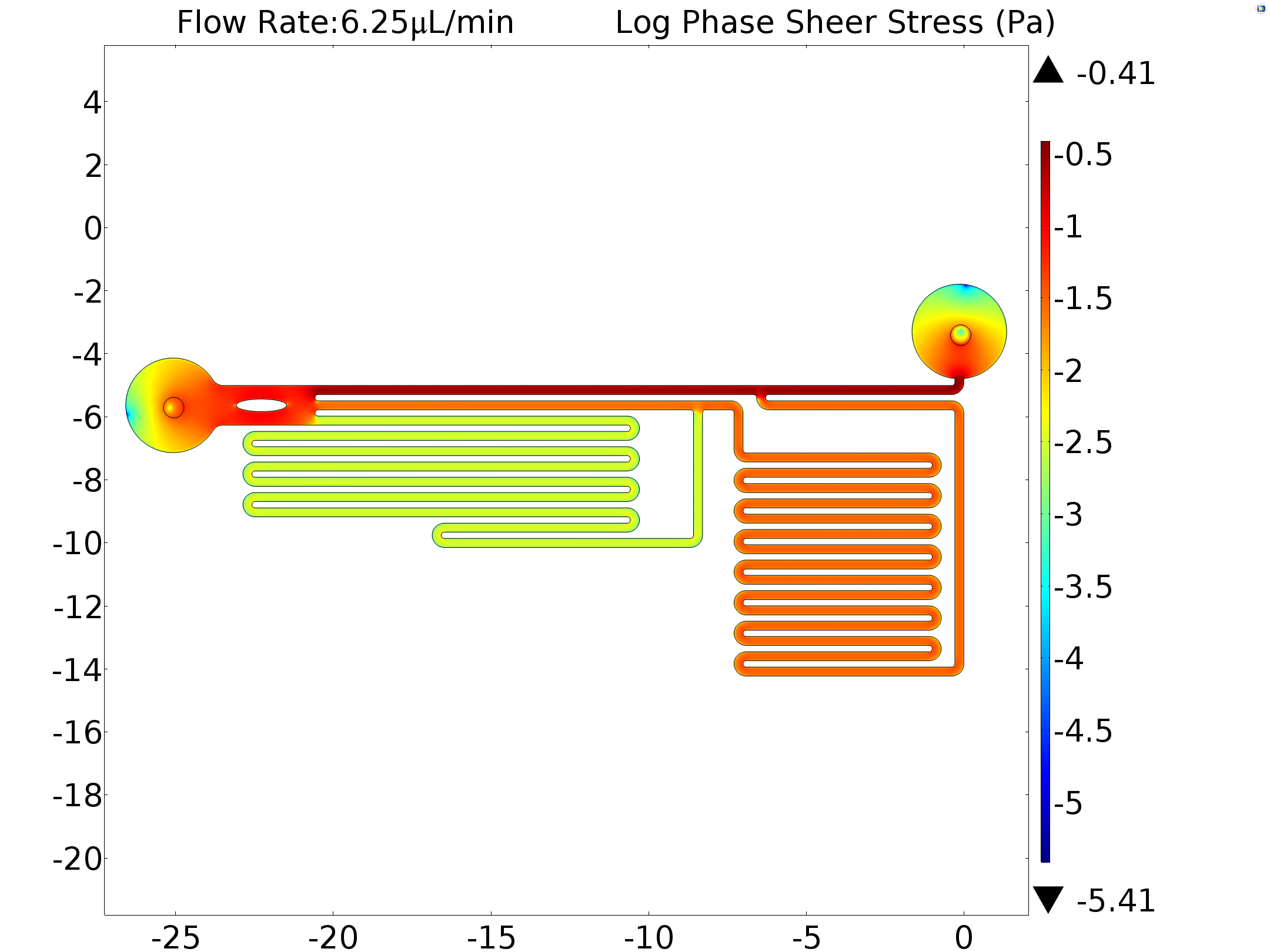
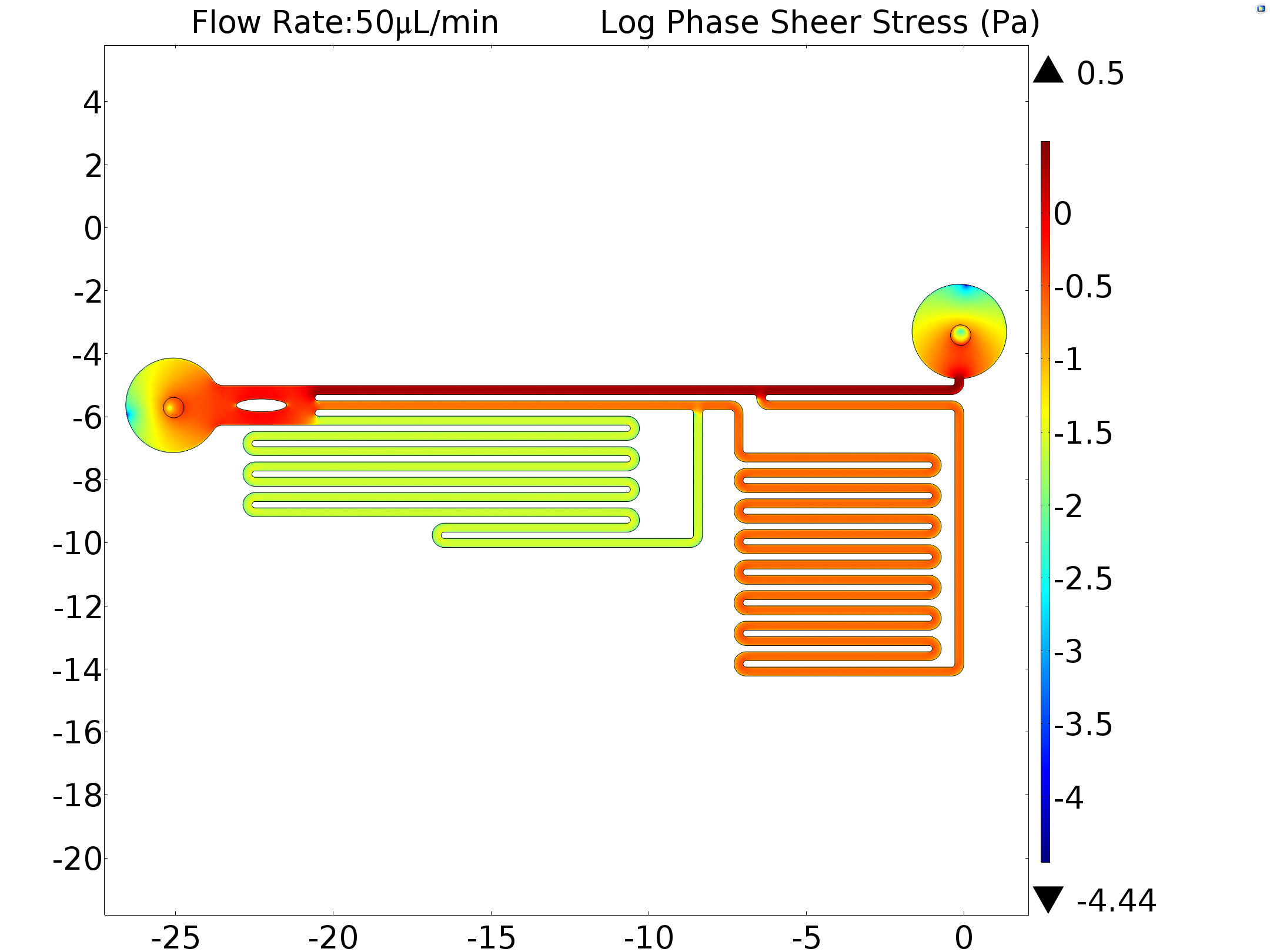
g. Final Shear Stress Calculation

In order to obtain the exact sheer force applied to the cells by the fluid flow. We input the experimentally used flow rate as a boundary condition in our model, which have already been tested before by comparing real-life experimental results with the simulation results (see Calibration), to calculate the sheer stress on the bottom of the channel where the cells can adhere to.

The inlet circle was given the velocity of 3.1392E-4 m/s and 0.0025113 m/s, which will give us the rate of flow values of 6.25μL/min and 50μL/min, which have been actually used to stimulate the cells in our experiments. And the outlet circle was given the pressure of 0.

The distribution of the sheer stress on the bottom plane is shown below.

Fig. 18 shear Stress Distribution Under Input Flow Rate 25μL/min (log scale)

Fig. 19 shear Stress Distribution Under Input Flow Rate 50μL/min (log scale)

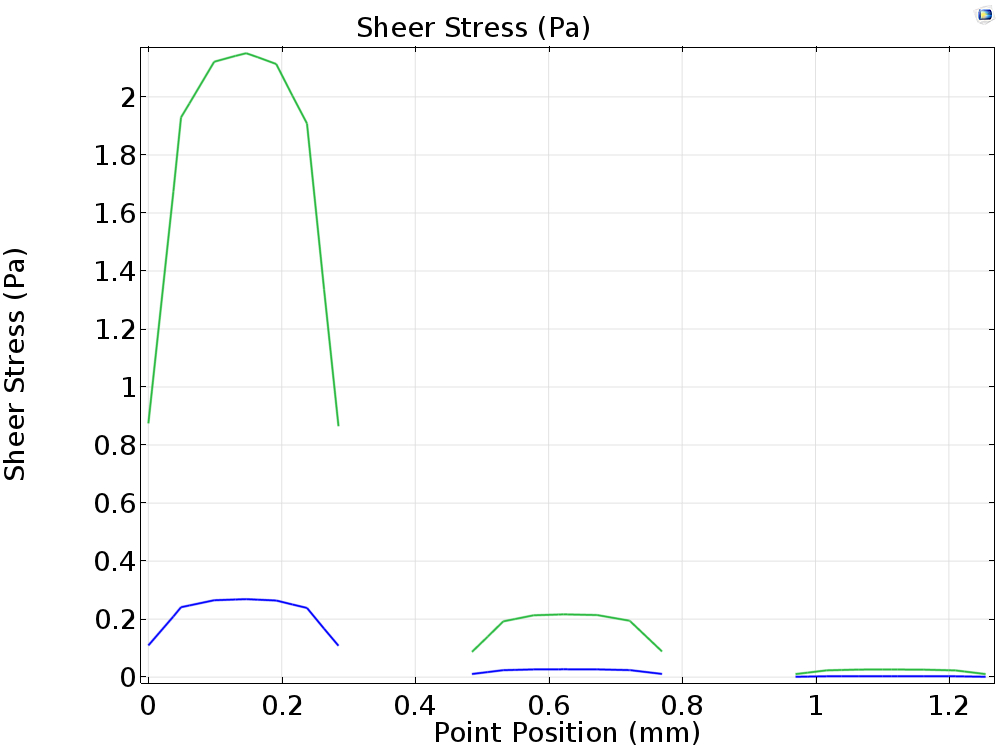
In order to further show the sheer stress difference under different parameters, we draw a cut line on the bottom plane from (-16, -4) to (-16, -6.45) crossing through three microfluidic channels in the observation zone. and plot the sheer stress on that line.

Fig. 20 Cut Line Drawn

Fig. 21 shear Stress Distribution on The Cut Line

The speed at the central line in all three channels at three different flow rate is listed below.

Channel Flow Rate	fast	middle	slow
6.25μL/min	0.26879Pa	0.02704Pa	0.00330Pa
50μL/min	2.15057Pa	0.21642Pa	0.02641Pa

Table 4 Simulation Results of Central Line shear Stress

Made by from the iGEM team SUSTech_Shenzhen.

Licensed under CC BY 4.0.

• ©2016 SUSTech_Shenzhen