Team:SUSTech Shenzhen/Model/Sound

Model

Sound Pressure Distribution

Introduction

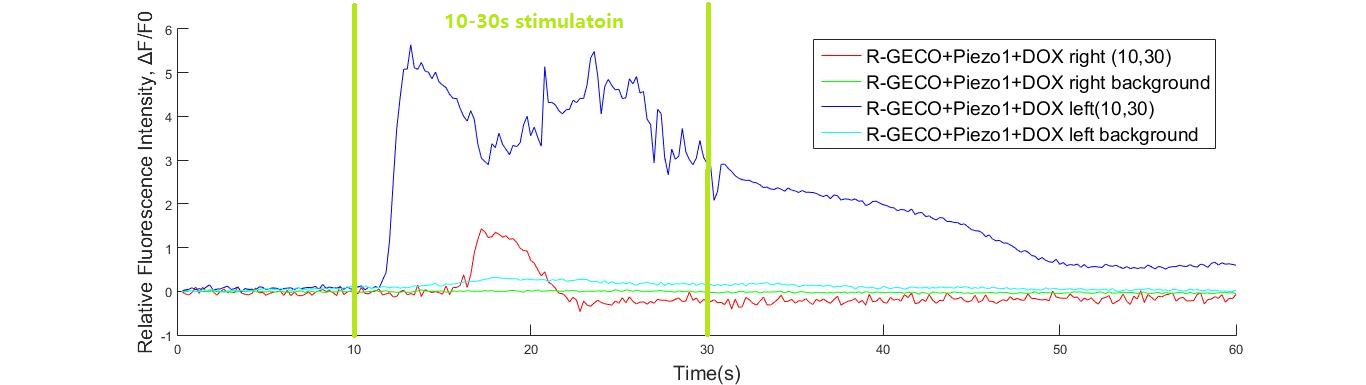
Sonic and ultrasonic waves could generate a pressure field to the cells adhering to the bottom of the cell dish. In our study of the sensitivity of mechanosensitive (MS) channel, we really found a most efficient sound frequency using 108KHz ultrasonic transducer and around 80V driving voltage. However, to quantitatively define the relationship of channel opening (considering the influence of energy or force difference), it was important to know the pressure field distribution on the cell layer with a certain device configuration. Mathematical analysis and finite element analysis (FEA) were used to define the modeling.

Firstly, a function was studied to give pressure on the surface of the ultrasonic transducer-water interface knowing the input voltage. Based on the interface pressure and physical properties of device, we constructed FEA models to simulate the ultrasonic radiant pressure field of the cell layer. Pressure field was studied in conditions of diverse power and distance between transducer interface and cell layer.

Fig. 1 Cell fluorescence response for 108KHz stimulation. The stimulation began at 10s and lasts for 20s. The fluorescence intensity increased to more than 5 times stronger than background.

108KHz Ultrasonic Pressure Modeling

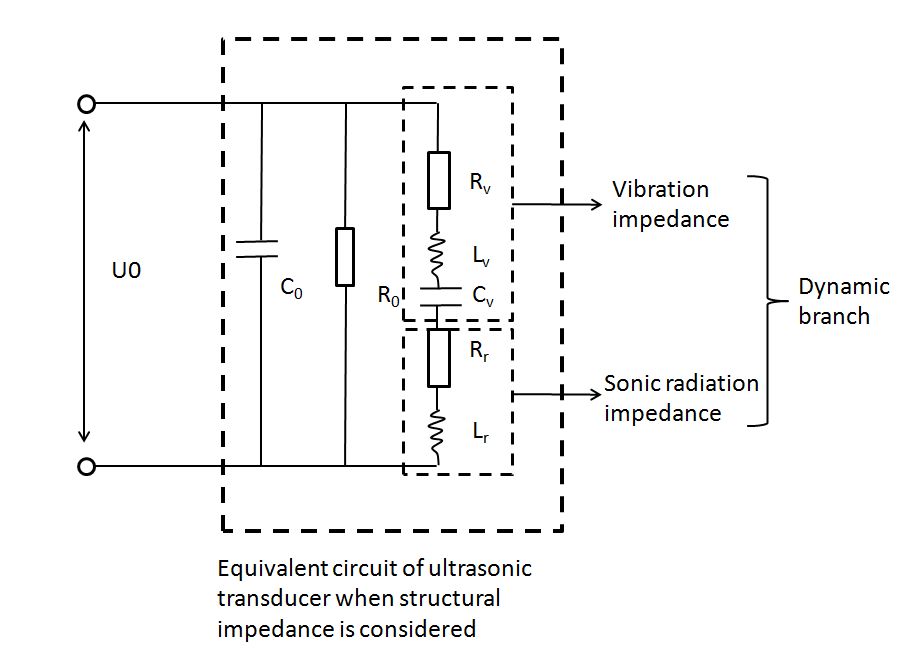
In this part, ultrasonic radiant pressure field for 108KHz transducer is modeled. In experiment, the 108KHz ultrasonic transducer was drenched into cell dish 1mm above cell layer for ultrasonic stimulation. The following is the equivalent circuit of an ultrasonic transducer.

Fig. 2 A The equivalent circuit of ultrasonic transducer, for low power condition (<500W), R₀ is very large and C₀ very small. The ultrasoinc radiation power is consumed by sonic radiation impedance. Dielectric and mechanical power is consumed by vibration impedance.

Fig. 2 B To measure the total power of transducer, U₀ and U_rm in fig. B were measured using oscilloscope. Rm=100Ω.

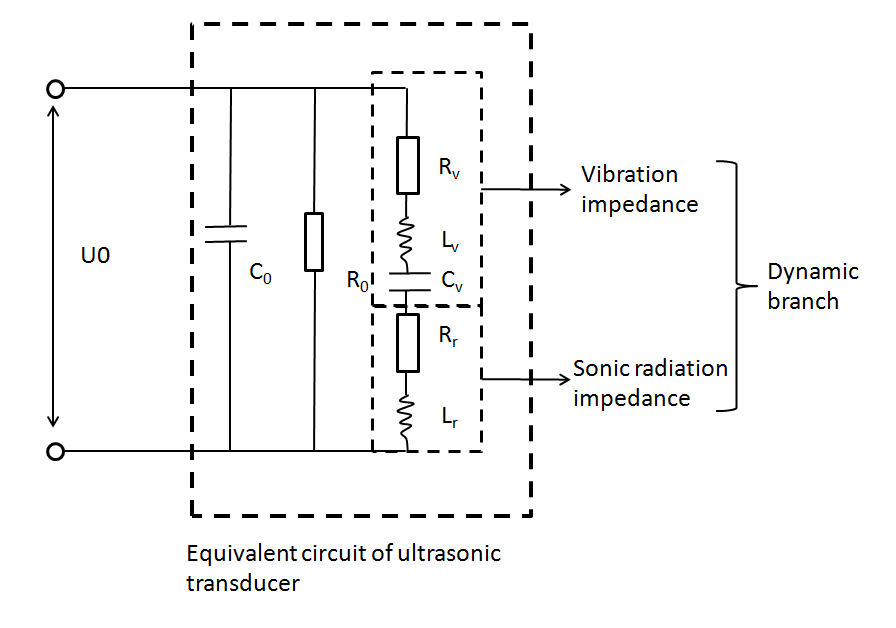
To calculate the power of transducer, we measured voltages using oscilloscope.

U_o= 79.6V

U_p-p=34.2V

U_o is the peak to peak voltage of transducer and its waveform was close to sinusoidal wave. U_p-p is the peak to peak voltage between the two ends of R_m which was serial to the transducer, and its waveform was close to sinusoidal wave triangle wave.

Thus, the effective voltage was

U_{\text{rm}} = \frac{1}{2T}\int_{0}^{\frac{T}{2}}{U_{\text{rm}}\text{dt}}

U_{\text{rm}} = \frac{1}{4T}\int_{0}^{\frac{T}{4}}{\frac{{4tU}_{p - p}}{T}\text{dt}}

So,

U_{\text{rm}} = \frac{U_{p - p}}{4} = 8.8V

The effective current I_eff

I_{\text{eff}} = \frac{U_{\text{rm}}}{R_{m}} = \frac{8.8V}{100\Omega} = 88mA

As U_o= 79.6V, and its waveform was close to sinusoidal wave. We have effective power

W_{\text{total}} = \frac{U_{0}I_{\text{eff}}}{\sqrt{2}} = 4.8W

For ultrasonic transducer, not all power is sonic radiation power.

W_{\text{total}} = W_{a} + W_{\text{el}} + W_{\text{ml}}

W_a , W_el, W_ml are respectively radiation power, dielectric power and mechanical power.

According to references, we toke the acoustic-electric efficiencyη_ae=0.85.

Then, we have the acoustic power W_a

W_{a} = \eta_{\text{ae}}W_{\text{total}} = 0.85 \times 4.8W = 4.1W

We assume the ultrasonic energy was evenly distributed on the transducer interface, that is:

<math>I\left( x,y,z = 0 \right) = \left\{ \begin{matrix} I_{0},x^{2} + y^{2} \leq R^{2} \\ 0,x^{2} + y^{2} > R^{2} \\ \end{matrix} \right.\ </math>

Where I₀ is the absolute ultrasound intensity, R is the radio of transducer interface, here R=8.0mm.

For the interface, we have power intensity I₀:

I_{0} = \frac{W_{a}}{\pi R^{2}} = \frac{4.1W}{\pi \times {(8.0 \times 10^{- 3})}^{2}} = 2.04W/\text{cm}^{2}

According to power intensity and pressure relation:

I_{0} = \frac{{P_{0}}^{2}}{2c\rho}

In which P₀ , c, \text{ρ\ }are respectively absolute pressure, acoustic velocity and water density.

P_{0} = \sqrt{2c\rho I_{0}} =ectively pressure on the transducer interface, sound speed in water, water density. We have, \sqrt{2 \times 1488 \times 1000 \times 2.04 \times 10^{4}}Pa = 2.46 \times 10^{5}\text{Pa}

Finite element analysis (FEA) was used to simulate the absolute pressure field on the cell layer. The following are the parameters set for simulation:

Parameter	Value	Description
dis	1.00mm	The distance between transducer interface and cell layer.
R	8.00mm	Radio of transducer interface
P0	2.46 \times 10^{5}\text{Pa}	Pressure on transducer interface
F0	108KHz	Frequency

The mesh was set as following:

'Fig. 3 Mesh for transducer drenched in cell dish, 1mm above cell layer.

The region near the transducer was divided into very small grids keeping scale at least 5 times smaller than the wave length (1.5cm). While regions near the cell dish wall was modeled roughly for higher simulating speed.

FEA simulation result:

Fig. 4 3D pressure field distribution for 108KHz transducer device.

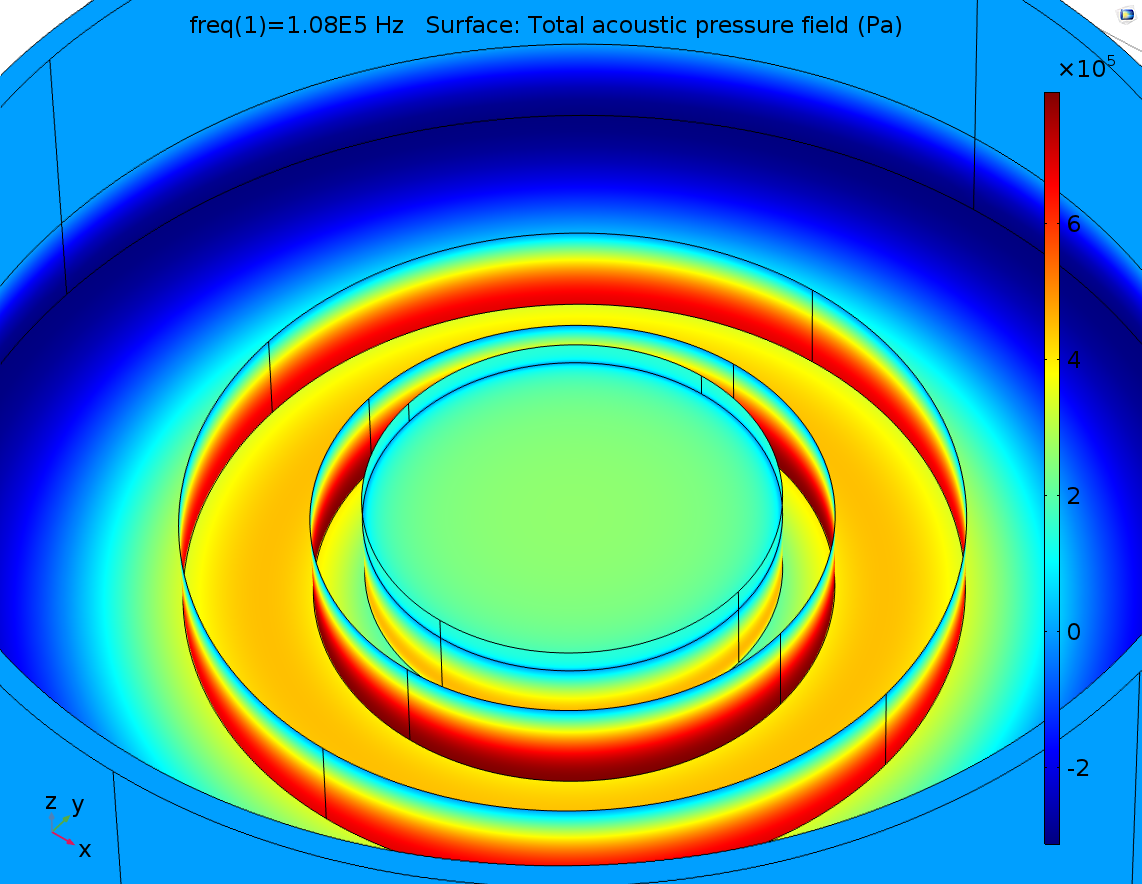
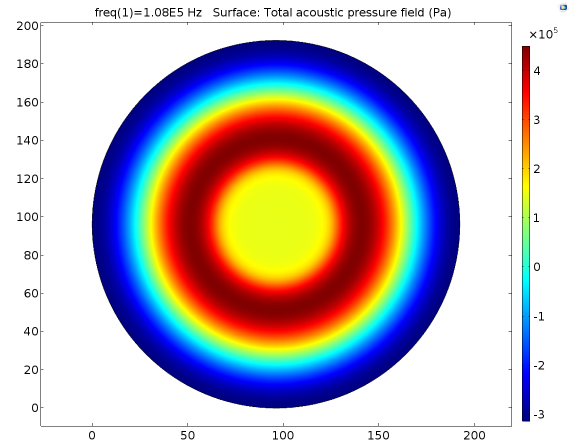
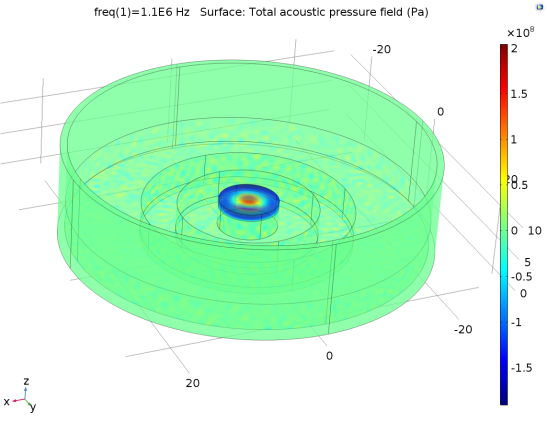
Pressure distribution on the bottom cell layer:

It was observed that pressure outside the transducer region reach a maximum value, which was not expected before simulation. In experiment we only observe the center of the cell dish that was just below the center of transducer.

Fig. 5 2D Pressure field distribution on the cell layer for 108KHz stimulation, and 251700 transducer-culture medium interface pressure.

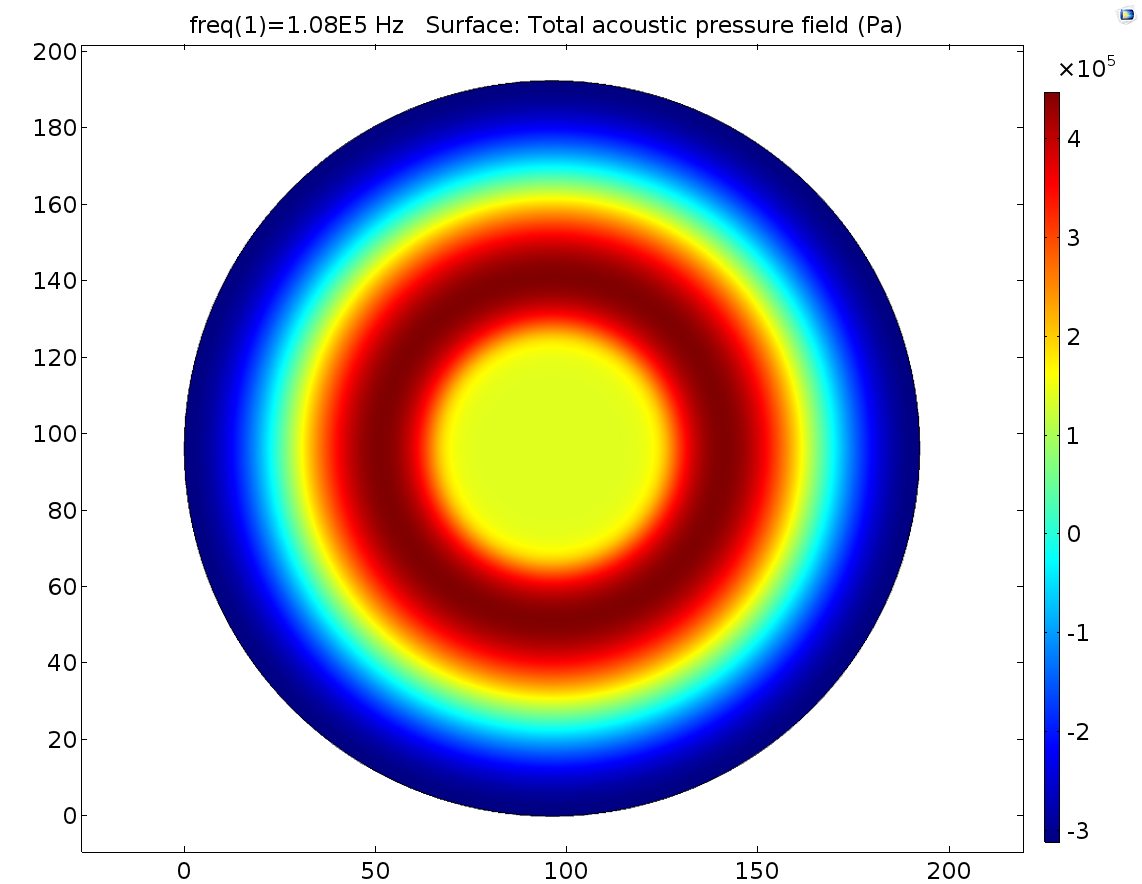
As the distance between transducer interface and cell layer may vary a little due to device configuration error, Pressure distribution patterns in condition of +-0.2mm distance error were also simulated to show the effect of distance error on pressure distribution pattern.

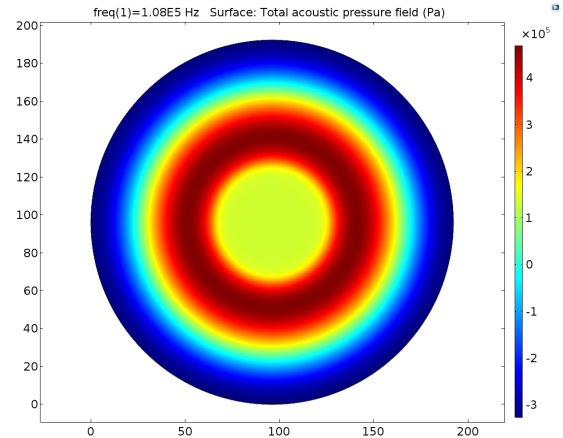
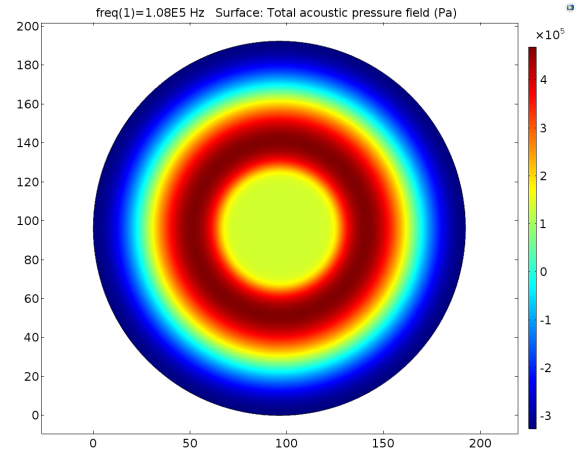
A

Fig. 6 A

B

Fig. 6 B

C

Fig. 6 C

Fig. 6 Pressure distribution of cell layer caused by 108KHz transducer, and its interface pressure were all set to be 251700Pa. The Transducer-water interface and cell layer were set as A 0.8mm, B 1.0mm, C 1.2mm respectively. The pressures of the center of cell layer were 1.35*10^5Pa, 1.40*10^5Pa, 1.48*10^5Pa respectively. So the error of distance for no more than 0.2mm may cause about 5.7% pressure change on the cell layer.

1.1MHz ultrasonic Pressure Modeling

The pressure distribution of 1.1MHz ultrasonic transducer was also modeled. Unlike the model above that merely gives a pressure distribution in a certain power. This modeling gives a function between input voltage and ultrasonic pressure distribution pattern. The influence of distance error was also discussed in this modeling. The transducer we use had been calibrated that U=23V, I₀=1.9W/cm² 3mm far from transducer surface.

Fig. 7 A

Fig. 7 B

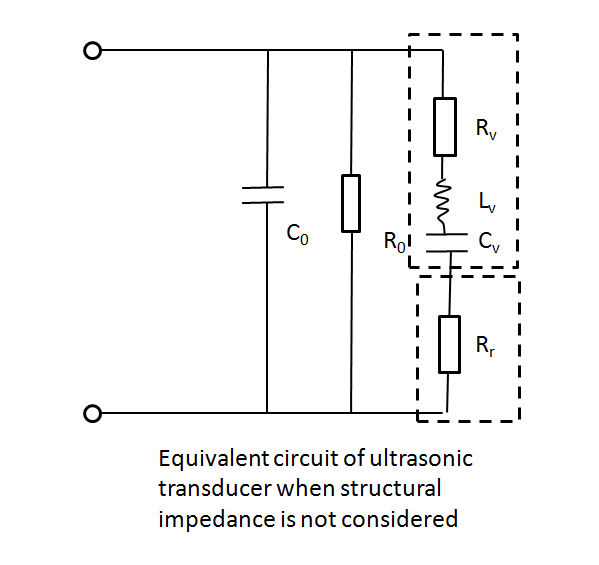
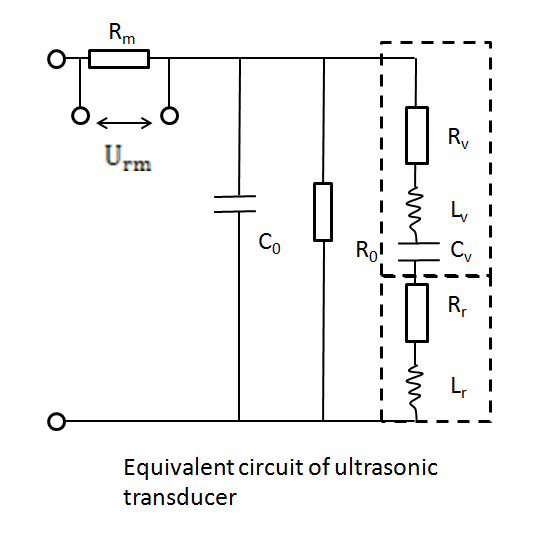
Fig. 7 Equivalent circuit of ultrasonic transducer in loading condition. A. Structural impedance is considered. B Structural impedance is considered.

When the structural impedance is considered, the dynamic branch resistance is Rv+Rr. When the structural impedance is considered, the dynamic branch resistance is Rr.

The sonic radiation power W_a is:

W_{a} = \frac{U^{2}}{{(R_{v} + R_{r})}^{2}}R_{r}

Ultrasound intensity:

I_{0} = \frac{W_{a}}{\pi R^{2}}

As we also have:

I_{0} = \frac{{P_{0}}^{2}}{2c\rho}

Let t=\frac{R_{r}}{{(R_{v} + R_{r})}^{2}}

I = \frac{tU^{2}}{\pi R^{2}}

According to the calibration:

U=23V, I=1.9*10^4W/m^2

We have:

t = \frac{\pi R^{2}I}{U^{2}} = \frac{\pi \times {(4.25 \times 10^{- 3})}^{2} \times 1.9 \times 10^{4}}{23^{2}} = 2.038 \times 10^{- 3}\text{\ Ω}^{- 1}

Here we assume the sound pressure 3mm far from the transducer interface is the same as that on the surface, which makes scene based on ANSYS simulation.

So,

p_{0} = \sqrt{\frac{2c\rho t}{\pi R^{2}}}U_{0} = \sqrt{\frac{2 \times 1488 \times 1000 \times 0.002038}{\pi \times {0.00425}^{2}}}U_{0} = 1.034 \times 10^{4}U_{0}\ Pa/V

So we have pressure-voltage relationship:

Voltage	Pressure on transducer-water interface	Pressure distribution on cell layer.
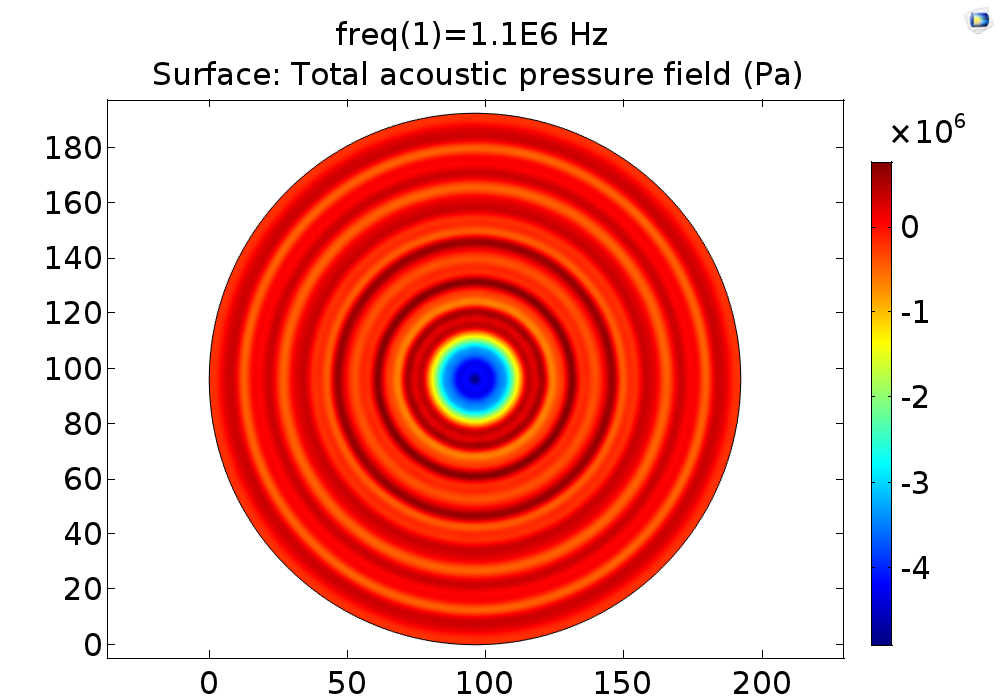
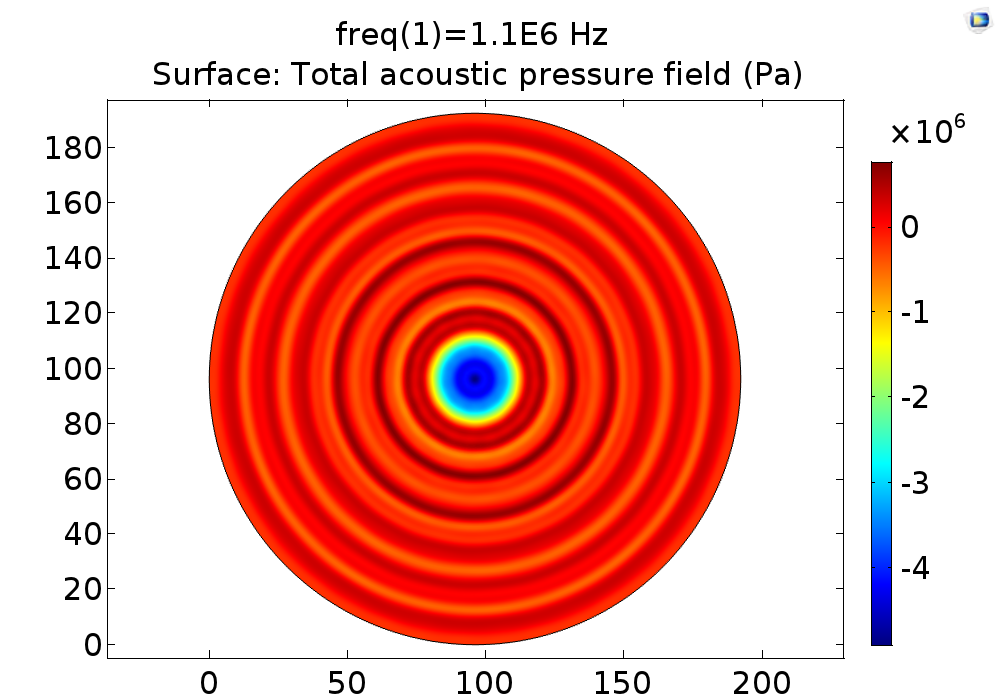
23V	2.378*10^5Pa	Fig. 10 A
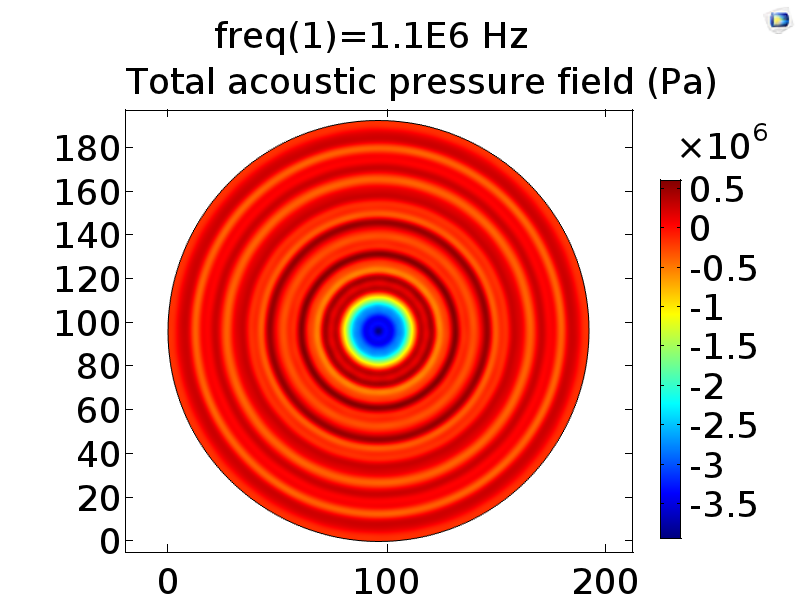
50V	5.17*10^5Pa	Fig. 10 B
60V	6.20*10^5Pa	Fig. 10 C

Simulation parameters:

Parameter	Value	Description
Dis	1.00mm	The distance between transducer interface and cell layer.
R	4.25mm	Radio of transducer interface
P0	2.38 \times 10^{5}\text{Pa}	Pressure on transducer interface
	5.17 \times 10^{5}\text{Pa}
	6.20 \times 10^{5}\text{Pa}
F0	1.1MHz	Frequency

The mesh was set as following:

Fig. 8 Mesh established for 1.1MHz transducer stimulation model.

FEA simulation result:

Fig. 9 3D pressure field distribution for 1.1MHz transducer device.

Pressure distribution on the bottom cell layer in conditions of different stimulation power:

A

Fig. 10 A

B

Fig. 10 B

C

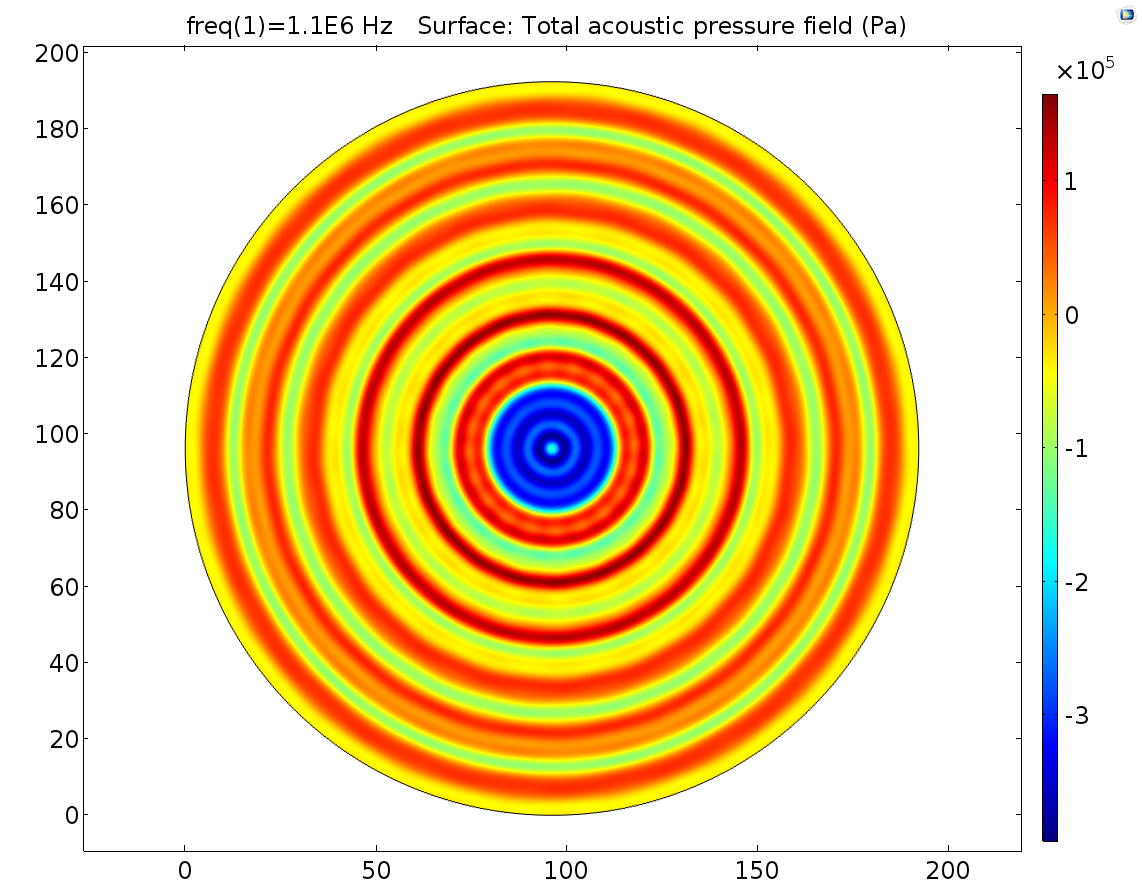
Fig. 10 C

Fig. 10 Pressure field distribution on cell layer in conditions of 40V input, that is 4.2*10^5Pa on the transducer interface (A), 50V 5.3*10^5Pa (B), 60V 6.3*10^5Pa (C). It’s found that the increase of stimulation pressure does not change the pressure field distribution pattern and only the amplitude of pressure of each position was amplified proportionally to stimulation pressure.

In experiment, it was impossible to keep the distance between transducer interface and cell layer being precisely 1.0mm. It’s important to study how sensitive the pressure field distribution was to the distance error. Thus, Pressure distribution patterns in condition of +-0.2mm distance error were simulated to show the influence of distance error on pressure distribution pattern. Here follows the simulation result. In these simulations, the transducer interface pressure and other parameters other than distance are all the same.

A

Fig. 11 A, 0.8mm distance

B

Fig. 11 B, 1.0mm distance

C

Fig. 11 C, 1.2mm distance

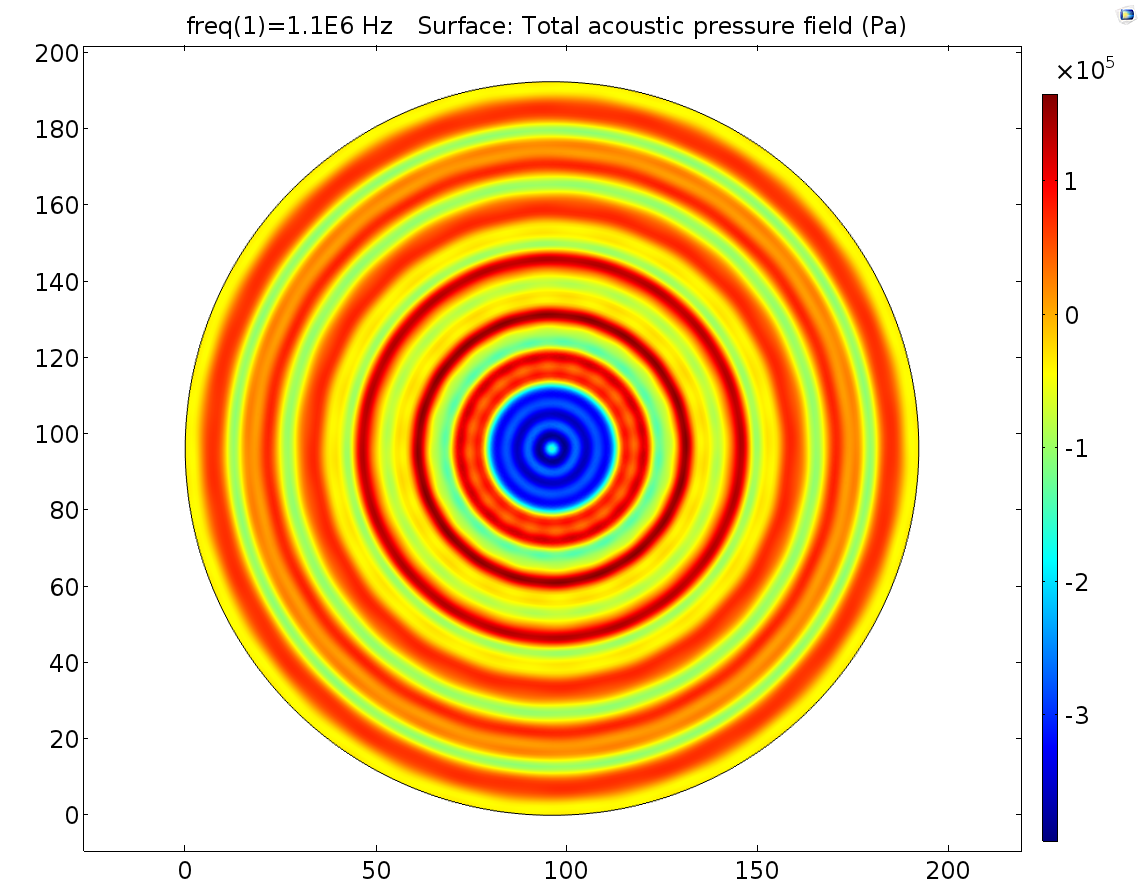
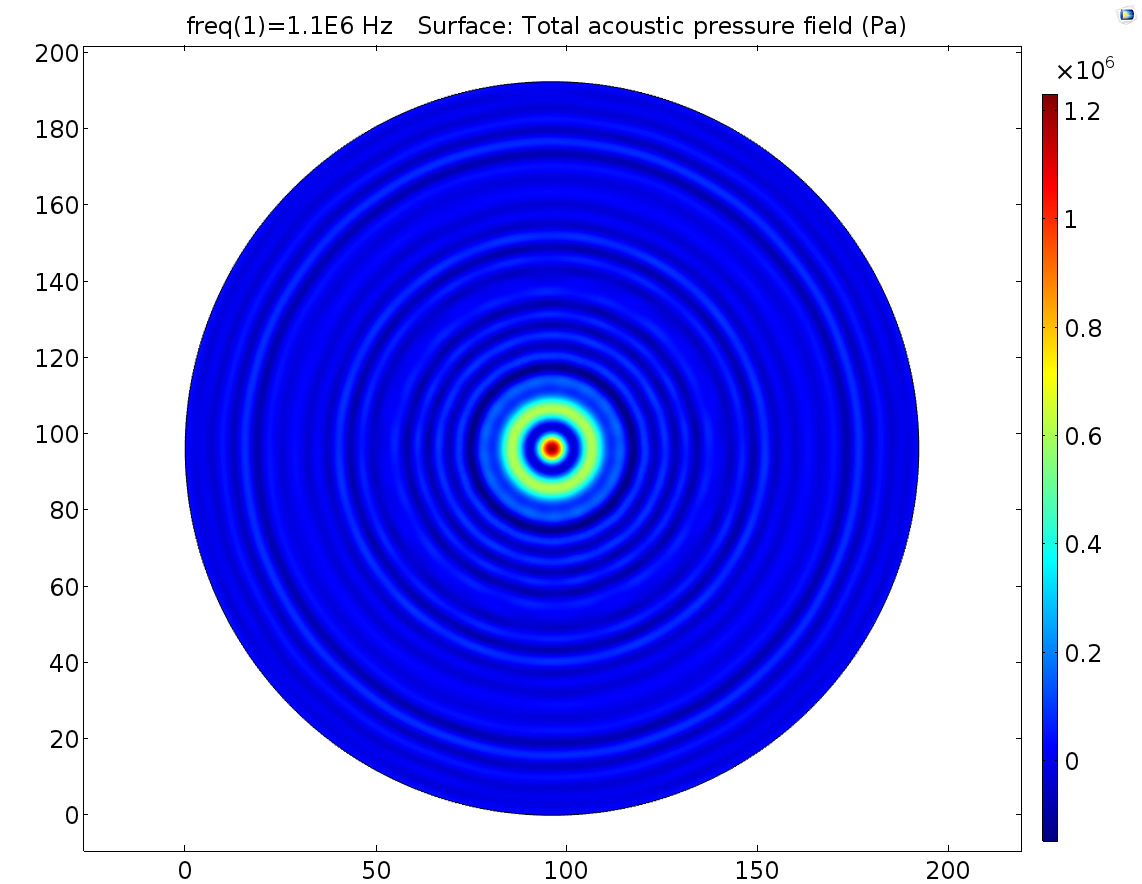
Fig. 11 0.8mm distance and 1.2mm distance 2D cell dish. The distance in A is , in B is 1.0mm, in C is 1.2mm. Other parameters are all the same.

From Fig. 11, we found that pressure distribution pattern of 1.1MHz ultrasound was a chaos. A little distance distortion can cause pressure distribution pattern changing greatly. The absolute pressure can’t be predicted by FEM simulation. 1.1MHz pressure is also not recommended for quantitative pressure-cell response relationship study.

Conclusion:

In this modeling, two ultrasonic devices were modeled to get the pressure field distribution for 108KHz and 1.1MHz frequencies. The pressure distribution of 108KHz transducer device is quite smooth and uniform just beneath the transducer interface. +-0.2mm/1mm (20%) displacement only leads to no more than 6% pressure change. While for 1.1MHz transducer stimulator, +-0.2mm displacement leads to completely different pressure field pattern. In all, the 108KHz ultrasonic transducer was recommended as ultrasonic stimulator for quantitative measure cell response.

References

Made by from the iGEM team SUSTech_Shenzhen.

Licensed under CC BY 4.0.

• ©2016 SUSTech_Shenzhen