| Line 72: | Line 72: | ||
<img src="https://static.igem.org/mediawiki/2016/7/76/British_Columbia_Modeling_Equation_1.png" | <img src="https://static.igem.org/mediawiki/2016/7/76/British_Columbia_Modeling_Equation_1.png" | ||
| − | style="width: 150px; display: table; margin: 0 auto; max-width: 100%"><p align="right"> | + | style="width: 150px; display: table; margin: 0 auto; max-width: 100%"><p align="right">Equation 1: Monod Kinetics for Substrate Limited Growth</p> |
| − | <p>The maximum specific growth rate and saturation constant can be obtained for our system by evaluating the growth rates for a range of initial substrate concentrations for each strain desired in the model. With a series of biomass concentration values over a range of time, plotting the natural logarithm of each biomass concentration produces a linear plot with a slope equal to the strain growth rate on substrate. With several growth rates as a function of substrate concentrations, the inverse of both the rate and the substrate concentration can be plotted to produce a Lineweaver-Burk plot. The slope of this plot is equal to K<sub>s</sub>/μ<sub>max</sub>, while the intercept is equal to 1/μ<sub>max</sub>. The C. crescentus data is obtained using this method, seen in Figure 1. </p> | + | <p>The maximum specific growth rate and saturation constant can be obtained for our system by evaluating the growth rates for a range of initial substrate concentrations for each strain desired in the model. With a series of biomass concentration values over a range of time, plotting the natural logarithm of each biomass concentration produces a linear plot with a slope equal to the strain growth rate on substrate. With several growth rates as a function of substrate concentrations, the inverse of both the rate and the substrate concentration can be plotted to produce a Lineweaver-Burk plot. The slope of this plot is equal to K<sub>s</sub>/μ<sub>max</sub>, while the intercept is equal to 1/μ<sub>max</sub>. The C. crescentus data is obtained using this method, seen in Figure 1. An analysis of this plot produced μ<sub>max</sub> of 0.156 hr<sup>-1</sup> and a K<sub>s</sub> of 0.403mM.</p> |
<img src="https://static.igem.org/mediawiki/2016/0/07/Lineweaver-Burk_Plot.png" | <img src="https://static.igem.org/mediawiki/2016/0/07/Lineweaver-Burk_Plot.png" | ||
style="width: 650px; display: table; margin: 0 auto; max-width: 100%"><p align="justify">Figure 1: Lineweaver-Burk plot for <i>C.crescentus</i> with initial glucose concentrations of 2.77, 5.56, 11.1, 22.2 M </p> | style="width: 650px; display: table; margin: 0 auto; max-width: 100%"><p align="justify">Figure 1: Lineweaver-Burk plot for <i>C.crescentus</i> with initial glucose concentrations of 2.77, 5.56, 11.1, 22.2 M </p> | ||
| + | <p>Differential equations using these constants can be made for the change in species concentration as a function of time, seen in Equation 2. The experimentally determined growth rate seemed to decrease as a function of cell density, and as a result, a penalty function of the inverse natural exponent to the power of cell density was included in the differential equation. The inclusion of a penalty function improved the relationship between modeled values and experimentally obtained values. The final model correlation can be seen in Figure 2.</p> | ||
| − | + | <img src="https://static.igem.org/mediawiki/2016/1/16/British_Columbia_Glucose_Caulobacter.png" | |
| − | + | style="width: 650px; display: table; margin: 0 auto; max-width: 100%"><p align="justify">Figure 2: Comparison of experimental data to modeled results for <i>C.crescentus</i> with initial glucose concentrations of 2.77, 5.56, 11.1, 22.2 M </p> | |
| − | <p></p> | + | |
<p>To model the rate of cellulose degradation into glucose through the expressed enzyme activity, a modified Michaelis-Menten relationship is used. Since cellulase enzymes are expressed on the surface of C. Crescentus, a relationship between glucose formation, cell concentration and enzyme expression must be made. To accomplish this, cellulase activity was tracked for two different cell concentrations, for a number of different substrate concentrations. The inverse of substrate degradation rate can be plotted against the inverse initial substrate concentrations to produce a Lineweaver-Burk plot. The slope of this plot is the Michaelis-Menten constant, KM, divided by the maximum rate of consumption, Vmax. Typically, Vmax is a constant related to enzyme concentration and kinetics, however in the consortium system, enzyme concentration changes as a function of time based on the concentration of C. crescentus in the system. Instead, Vmax is a combination of enzyme activity, the number of enzymes expressed per C. crescentus, and the concentration of C. crescentus, seen in Equation ###. The activity and expression number can be assumed constant, represented by β. To determine the constants in our Michaeles-Menten kinetics, two Lineweaver-Burk plots are created with two different cell concentrations. The difference between the y axis intercept values can be used to determine the constant β, and the slope can be used to determine KM. Using this information, the ordinary differential equation describing cellulose degradation can be developed. </p> | <p>To model the rate of cellulose degradation into glucose through the expressed enzyme activity, a modified Michaelis-Menten relationship is used. Since cellulase enzymes are expressed on the surface of C. Crescentus, a relationship between glucose formation, cell concentration and enzyme expression must be made. To accomplish this, cellulase activity was tracked for two different cell concentrations, for a number of different substrate concentrations. The inverse of substrate degradation rate can be plotted against the inverse initial substrate concentrations to produce a Lineweaver-Burk plot. The slope of this plot is the Michaelis-Menten constant, KM, divided by the maximum rate of consumption, Vmax. Typically, Vmax is a constant related to enzyme concentration and kinetics, however in the consortium system, enzyme concentration changes as a function of time based on the concentration of C. crescentus in the system. Instead, Vmax is a combination of enzyme activity, the number of enzymes expressed per C. crescentus, and the concentration of C. crescentus, seen in Equation ###. The activity and expression number can be assumed constant, represented by β. To determine the constants in our Michaeles-Menten kinetics, two Lineweaver-Burk plots are created with two different cell concentrations. The difference between the y axis intercept values can be used to determine the constant β, and the slope can be used to determine KM. Using this information, the ordinary differential equation describing cellulose degradation can be developed. </p> | ||
Revision as of 02:24, 18 October 2016
Modelling
Introduction
A model was developed to describe a mixed culture of C. crescentus and E.coli with cellulose and glucose as the primary feedstocks. In mixed culture systems, the dynamics between the species can impact the complexity of the model, with more sophisticated dynamics requiring significant effort. Two mixed culture dynamics exist in the consortia: competition, in which species compete for substrate, and commensalism, where one species requires the existence of another to survive. The commensalism is passive and has been assumed to have negligible impact on the growth of either culture.
The culture dynamics have been modeled using a system of four ordinary differential equations: one for each species, one for glucose consumption and formation, and one for cellulose degradation. To model our environment, the individual species growth, enzyme expression, and enzyme activity were experimentally determined at optimum co-culture conditions of 30 degrees Celsius. Using these values, ordinary differential equations for a mixed culture were developed assuming that both E. coli and C. crescentus behaved competitively and that cellulose degradation by expressed cellulase enzymes on the C. crescentus surface did not favor C. crescentus due to diffusion gradients.
Monod Kinetics
To model substrate limited growth, Monod kinetics provide a relationship between substrate concentration and species growth. Two constants, maximum specific growth rate and the saturation constant are required to use the relationship. The maximum specific growth rate of the culture, μmax, is the growth rate when substrate is in excess. The saturation constant, Ks, is the concentration at which the specific growth rate is half the maximum specific growth rate.

Equation 1: Monod Kinetics for Substrate Limited Growth
The maximum specific growth rate and saturation constant can be obtained for our system by evaluating the growth rates for a range of initial substrate concentrations for each strain desired in the model. With a series of biomass concentration values over a range of time, plotting the natural logarithm of each biomass concentration produces a linear plot with a slope equal to the strain growth rate on substrate. With several growth rates as a function of substrate concentrations, the inverse of both the rate and the substrate concentration can be plotted to produce a Lineweaver-Burk plot. The slope of this plot is equal to Ks/μmax, while the intercept is equal to 1/μmax. The C. crescentus data is obtained using this method, seen in Figure 1. An analysis of this plot produced μmax of 0.156 hr-1 and a Ks of 0.403mM.
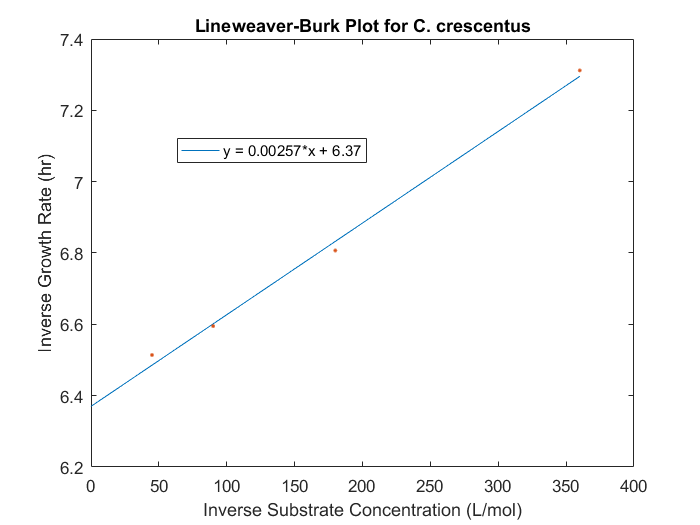
Figure 1: Lineweaver-Burk plot for C.crescentus with initial glucose concentrations of 2.77, 5.56, 11.1, 22.2 M
Differential equations using these constants can be made for the change in species concentration as a function of time, seen in Equation 2. The experimentally determined growth rate seemed to decrease as a function of cell density, and as a result, a penalty function of the inverse natural exponent to the power of cell density was included in the differential equation. The inclusion of a penalty function improved the relationship between modeled values and experimentally obtained values. The final model correlation can be seen in Figure 2.

Figure 2: Comparison of experimental data to modeled results for C.crescentus with initial glucose concentrations of 2.77, 5.56, 11.1, 22.2 M
To model the rate of cellulose degradation into glucose through the expressed enzyme activity, a modified Michaelis-Menten relationship is used. Since cellulase enzymes are expressed on the surface of C. Crescentus, a relationship between glucose formation, cell concentration and enzyme expression must be made. To accomplish this, cellulase activity was tracked for two different cell concentrations, for a number of different substrate concentrations. The inverse of substrate degradation rate can be plotted against the inverse initial substrate concentrations to produce a Lineweaver-Burk plot. The slope of this plot is the Michaelis-Menten constant, KM, divided by the maximum rate of consumption, Vmax. Typically, Vmax is a constant related to enzyme concentration and kinetics, however in the consortium system, enzyme concentration changes as a function of time based on the concentration of C. crescentus in the system. Instead, Vmax is a combination of enzyme activity, the number of enzymes expressed per C. crescentus, and the concentration of C. crescentus, seen in Equation ###. The activity and expression number can be assumed constant, represented by β. To determine the constants in our Michaeles-Menten kinetics, two Lineweaver-Burk plots are created with two different cell concentrations. The difference between the y axis intercept values can be used to determine the constant β, and the slope can be used to determine KM. Using this information, the ordinary differential equation describing cellulose degradation can be developed.
When the production of glucose through cellulose degradation and the consumption due to the growth of E. coli and C. crescentus are combined, the ordinary differential equation describing glucose utilization can be developed.
Check out other parts of our project below!



