| Line 51: | Line 51: | ||
<ul class="nav sidebar-nav nav-pills nav-stacked"> | <ul class="nav sidebar-nav nav-pills nav-stacked"> | ||
<li><a href="#Introduction">Introduction</a></li> | <li><a href="#Introduction">Introduction</a></li> | ||
| − | |||
<li><a href="#Model-Development">Model Development</a></li> | <li><a href="#Model-Development">Model Development</a></li> | ||
<li><a href="#Results">Results</a></li> | <li><a href="#Results">Results</a></li> | ||
| Line 66: | Line 65: | ||
<p>The culture dynamics have been modelled using a system of four ordinary differential equations: one for each species, one for glucose consumption and formation, and one for cellulose degradation. To model our environment, the individual species growth, enzyme expression, and enzyme activity were experimentally determined at optimum co-culture conditions of 30 degrees Celsius. Using these values, ordinary differential equations for a mixed culture were developed assuming that both <i>E. coli</i> and <i>C. crescentus</i> behaved competitively and that cellulose degradation by expressed cellulase enzymes on the <i>C. crescentus</i> surface did not favor <i>C. crescentus</i> due to diffusion gradients.</p> | <p>The culture dynamics have been modelled using a system of four ordinary differential equations: one for each species, one for glucose consumption and formation, and one for cellulose degradation. To model our environment, the individual species growth, enzyme expression, and enzyme activity were experimentally determined at optimum co-culture conditions of 30 degrees Celsius. Using these values, ordinary differential equations for a mixed culture were developed assuming that both <i>E. coli</i> and <i>C. crescentus</i> behaved competitively and that cellulose degradation by expressed cellulase enzymes on the <i>C. crescentus</i> surface did not favor <i>C. crescentus</i> due to diffusion gradients.</p> | ||
| − | <section id=" | + | <section id="Model Development" class="anchor"> |
| − | <h2> | + | <h2>Model Development</h2> |
<p>To model substrate limited growth, Monod kinetics provided a relationship between substrate concentration and species growth. Two constants, maximum specific growth rate and the saturation constant, are required to use the relationship. The maximum specific growth rate of the culture, μ<sub>max</sub>, is the growth rate when substrate is in excess. The saturation constant, K<sub>s</sub>, is the concentration at which the specific growth rate is half the maximum specific growth rate. </p> | <p>To model substrate limited growth, Monod kinetics provided a relationship between substrate concentration and species growth. Two constants, maximum specific growth rate and the saturation constant, are required to use the relationship. The maximum specific growth rate of the culture, μ<sub>max</sub>, is the growth rate when substrate is in excess. The saturation constant, K<sub>s</sub>, is the concentration at which the specific growth rate is half the maximum specific growth rate. </p> | ||
| Line 78: | Line 77: | ||
style="width: 650px; display: table; margin: 0 auto; max-width: 100%"><p align="justify">Figure 1: Lineweaver-Burk plot for <i>C.crescentus</i> with initial glucose concentrations of 2.77, 5.56, 11.1, 22.2 M </p> | style="width: 650px; display: table; margin: 0 auto; max-width: 100%"><p align="justify">Figure 1: Lineweaver-Burk plot for <i>C.crescentus</i> with initial glucose concentrations of 2.77, 5.56, 11.1, 22.2 M </p> | ||
| − | |||
| − | |||
<p>Differential equations using the Monod growth rate can be made for the change in species concentration as a function of time, seen in Equation 2. The experimentally determined growth rate seemed to decrease as a function of cell density, and as a result, a penalty function of the inverse natural exponent to the power of cell density was included in the differential equation. The inclusion of a penalty function improved the relationship between modelled values and experimentally obtained values. The final model correlation can be seen in Figure 2.</p> | <p>Differential equations using the Monod growth rate can be made for the change in species concentration as a function of time, seen in Equation 2. The experimentally determined growth rate seemed to decrease as a function of cell density, and as a result, a penalty function of the inverse natural exponent to the power of cell density was included in the differential equation. The inclusion of a penalty function improved the relationship between modelled values and experimentally obtained values. The final model correlation can be seen in Figure 2.</p> | ||
| Line 90: | Line 87: | ||
style="width: 700px; display: table; margin: 0 auto; max-width: 100%"><p align="justify">Figure 2: Comparison of experimental data to modelled results for <i>C.crescentus</i> with initial glucose concentrations of 2.77, 5.56, 11.1, 22.2 M </p> | style="width: 700px; display: table; margin: 0 auto; max-width: 100%"><p align="justify">Figure 2: Comparison of experimental data to modelled results for <i>C.crescentus</i> with initial glucose concentrations of 2.77, 5.56, 11.1, 22.2 M </p> | ||
| − | <p></p> | + | <p>To obtain the maximum growth rate for the <i>E.coli</i> species, several <i>E.coli</i> cultures were compared to <i>C. crescentus</i> cultures grown at the same temperature and substrate conditions. In the absence of substrate limiting growth kinetics, with the same initial substrate concentration, the growth kinetics should differ based on the μ<sub>max</sub> of either species. Analysis of three triplicates for either species indicated that <i>E.coli</i> grew at a rate 2.58 times greater than <i>C. crescentus</i> in the same conditions, a result that can be directly related to μ<sub>max</sub>. The comparative growth curves can be seen in Figure 3. Based on these curves, the growth rate for <i>E.coli</i> is 3.1 times the growth rate for <i>C. crescentus</i>. The K<sub>M</sub> for <i>E.coli</i> was assumed to be similar to <i>C.crescentus</i>. The species differential equation, seen in Equation 2, is also used for <i>E.coli</i> development. A penalty function was also used for <i>E.coli</i>, allowing E.coli growth to match experimental data.</p> |
| + | |||
| + | <img src="https://static.igem.org/mediawiki/2016/9/9d/British_Columbia_Ecoli_Rate.png" | ||
| + | style="width: 700px; display: table; margin: 0 auto; max-width: 100%"><p align="justify">Figure 3: Comparison of E | ||
| + | .coli and C. crescentus growth rates in M2 media, with 22.2mM glucose in microwells.</p> | ||
<p></p> | <p></p> | ||
</div><!--.col-sm-9--> | </div><!--.col-sm-9--> | ||
Revision as of 15:38, 18 October 2016
Modelling
Introduction
A model was developed to describe a mixed culture of C. crescentus and E.coli with cellulose and glucose as the primary feedstocks. In mixed culture systems, the dynamics between the species can impact the complexity of the model, with more sophisticated dynamics requiring significant effort. Two mixed culture dynamics exist in the consortia: competition, in which species compete for substrate, and commensalism, where one species requires the existence of another to survive. The commensalism is passive and has been assumed to have negligible impact on the growth of either culture.
The culture dynamics have been modelled using a system of four ordinary differential equations: one for each species, one for glucose consumption and formation, and one for cellulose degradation. To model our environment, the individual species growth, enzyme expression, and enzyme activity were experimentally determined at optimum co-culture conditions of 30 degrees Celsius. Using these values, ordinary differential equations for a mixed culture were developed assuming that both E. coli and C. crescentus behaved competitively and that cellulose degradation by expressed cellulase enzymes on the C. crescentus surface did not favor C. crescentus due to diffusion gradients.
Model Development
To model substrate limited growth, Monod kinetics provided a relationship between substrate concentration and species growth. Two constants, maximum specific growth rate and the saturation constant, are required to use the relationship. The maximum specific growth rate of the culture, μmax, is the growth rate when substrate is in excess. The saturation constant, Ks, is the concentration at which the specific growth rate is half the maximum specific growth rate.

Equation 1: Monod Kinetics for Substrate Limited Growth
The maximum specific growth rate and saturation constant can be obtained for our system by evaluating the growth rates for a range of initial substrate concentrations for each strain desired in the model. With a series of biomass concentration values over a range of time, plotting the natural logarithm of each biomass concentration produces a linear plot with a slope equal to the strain growth rate on substrate. With several growth rates as a function of substrate concentrations, the inverse of both the rate and the substrate concentration can be plotted to produce a Lineweaver-Burk plot. The slope of this plot is equal to Ks/μmax, while the intercept is equal to 1/μmax. The C. crescentus data is obtained using this method, seen in Figure 1. An analysis of this plot produced μmax of 0.156 hr-1 and a Ks of 0.403 mM.
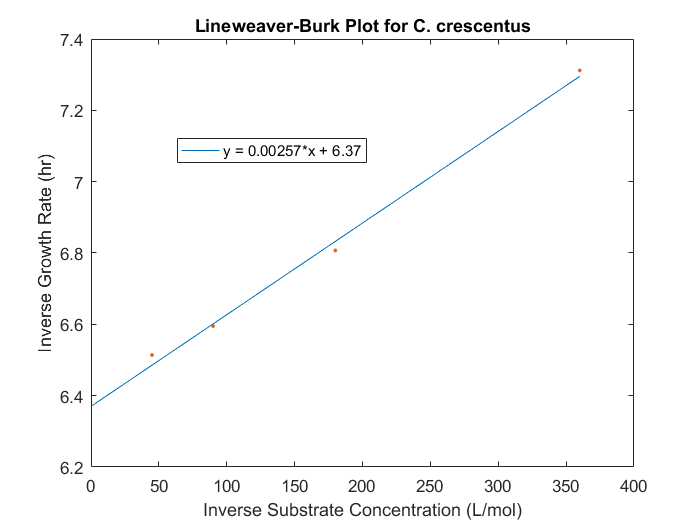
Figure 1: Lineweaver-Burk plot for C.crescentus with initial glucose concentrations of 2.77, 5.56, 11.1, 22.2 M
Differential equations using the Monod growth rate can be made for the change in species concentration as a function of time, seen in Equation 2. The experimentally determined growth rate seemed to decrease as a function of cell density, and as a result, a penalty function of the inverse natural exponent to the power of cell density was included in the differential equation. The inclusion of a penalty function improved the relationship between modelled values and experimentally obtained values. The final model correlation can be seen in Figure 2.

Equation 2: Differential Equation for Species Growth

Figure 2: Comparison of experimental data to modelled results for C.crescentus with initial glucose concentrations of 2.77, 5.56, 11.1, 22.2 M
To obtain the maximum growth rate for the E.coli species, several E.coli cultures were compared to C. crescentus cultures grown at the same temperature and substrate conditions. In the absence of substrate limiting growth kinetics, with the same initial substrate concentration, the growth kinetics should differ based on the μmax of either species. Analysis of three triplicates for either species indicated that E.coli grew at a rate 2.58 times greater than C. crescentus in the same conditions, a result that can be directly related to μmax. The comparative growth curves can be seen in Figure 3. Based on these curves, the growth rate for E.coli is 3.1 times the growth rate for C. crescentus. The KM for E.coli was assumed to be similar to C.crescentus. The species differential equation, seen in Equation 2, is also used for E.coli development. A penalty function was also used for E.coli, allowing E.coli growth to match experimental data.

Figure 3: Comparison of E .coli and C. crescentus growth rates in M2 media, with 22.2mM glucose in microwells.
Check out other parts of our project below!



