Difference between revisions of "Team:SUSTech Shenzhen/Model/Calibration"
| Line 51: | Line 51: | ||
! variable !! mean(um/s) !! variable !! std(um/s) | ! variable !! mean(um/s) !! variable !! std(um/s) | ||
|- | |- | ||
| − | | ex_fast_mean || 50850 || ex_fast_std || | + | | ex_fast_mean || 50850 || ex_fast_std || 8600 |
|- | |- | ||
| − | | ex_mid_mean || 5200 || ex_mid_std || | + | | ex_mid_mean || 5200 || ex_mid_std || 350 |
|- | |- | ||
| − | | ex_slow_mean || 676 | + | | ex_slow_mean || 676 || ex_slow_std || 170 |
|} | |} | ||
Revision as of 13:10, 17 October 2016
Test
test page
Calibration of fluid flow velocity
To visualize the flow profile, rainbow beads (SPHEROTM Rainbow Calibration Particles, diameter: 6um) were dissolved in the cell culture medium, which contained the dead cells. A series of pumped flow rate(5ul/min, 15ul/min, and 45ul/min) were applied to generate a steady fluid flow. The exposure time was set to 100ms so that the length of the streakline (shown as a gray line in picture) represented the total traveling distance of the beads during the exposure. Fig. 1 shows a typical image of a bead trace in the fast microfluidics channel with a pumped flow rate of 5ul/min. To minimize hydraulic effects of the PDMS walls, the pictures were taken from the midplane of the channel providing the maximum flow velocity. Note that the traveling direction of the beads was left. Each streak was measured separately, and the average length of all streaks in one particular channel divides the exposure time was regarded as the maximum flow velocity of this channel. [1]
Experiment
To minimize the error, we took pictures on fast microfluidics channel when pumped flow rate was 5ul/min; on mid microfluidics channel when pumped flow rate was 15ul/min; on slow microfluidics channel when pumped flow rate was 45ul/min, considering that fluid flow velocity is proportional to pumped flow rate.
Data collection blow:
| channel | flow rate(ul/min) | length①(um) | length②(um) | length③(um) |
|---|---|---|---|---|
| fast | 5 | 630 | 455 | 610 |
| mid | 15 | 180 | 160 | 180 |
| slow | 45 | 48 | 75 | 80 |
Result
We wrote a MatLab program to calculate the maximum flow velocities. Codes were shown below:
MatLab Code:
ex_fast=[630,455,610]*90;
% align the data to um/s by multiply 10 and convert to 45ul/min
ex_mid=[180,160,180]*30;
ex_slow=[48,75,80]*10;
ex_fast_mean=mean(ex_fast); ex_fast_std=std(ex_fast);
ex_mid_mean=mean(ex_mid); ex_mid_std=std(ex_mid);
ex_slow_mean=mean(ex_slow); ex_slow_std=std(ex_slow);
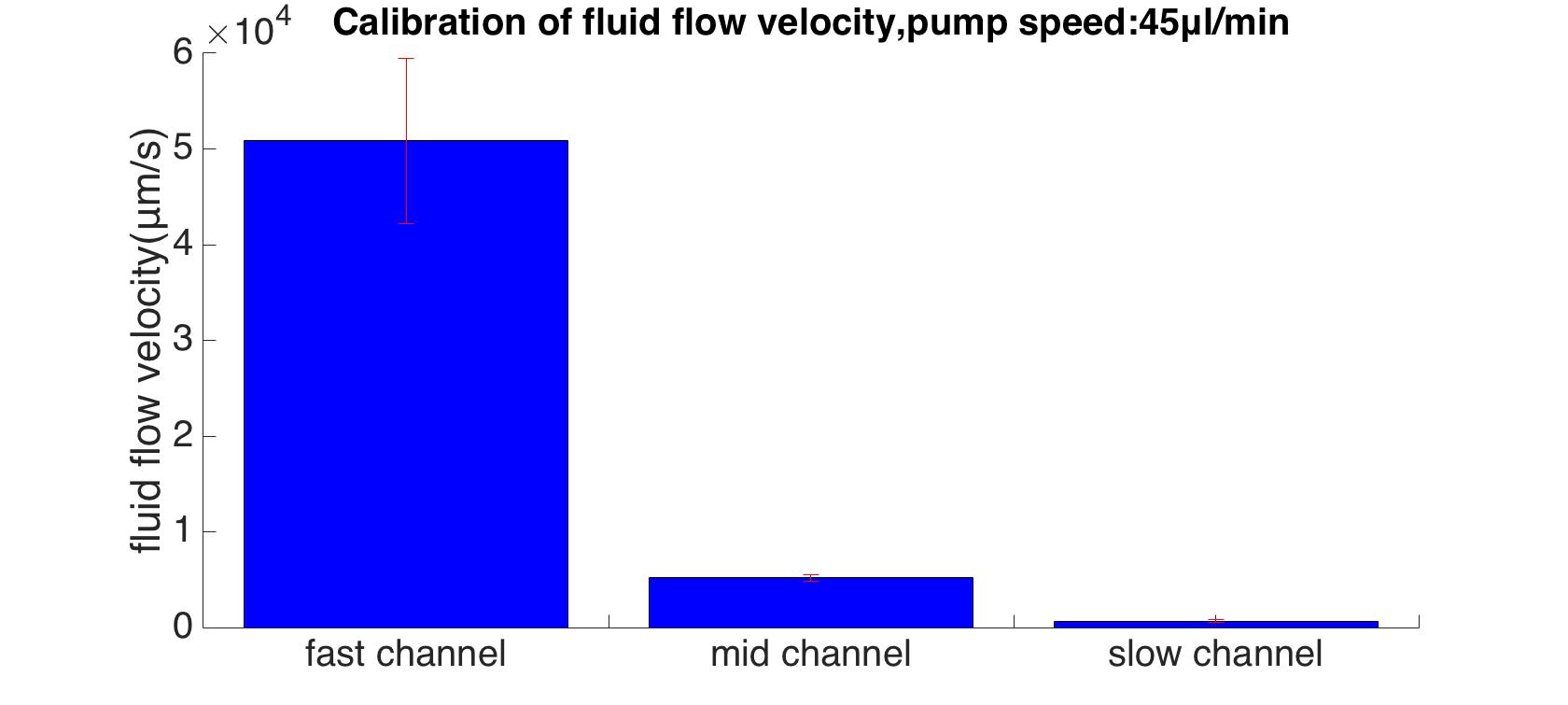
| variable | mean(um/s) | variable | std(um/s) |
|---|---|---|---|
| ex_fast_mean | 50850 | ex_fast_std | 8600 |
| ex_mid_mean | 5200 | ex_mid_std | 350 |
| ex_slow_mean | 676 | ex_slow_std | 170 |
The ratio of maximum velocities in 3 different channels is 13:100:978.
Reference
- ↑ Maneshi MM, Sachs F, Hua SZ, A Threshold Shear Force for Calcium Influx in an Astrocyte Model of Traumatic Brain Injury.J Neurotrauma. 2015 Jul 1, 32(13) : p. 1020-9.
