Team:SUSTech Shenzhen/Measurement

Measurement

Model

Introduction

Mechanosensitive channels (MS channel) are present in the cell membrane of both eukaryote and prokaryote and responsible for sensing mechanical stimuli，such as touch, hearing and balancing [1, 2]. Also, they participate in cardiovascular regulation and osmotic homeostasis. In our project, we aim to explore the MS channel’s relative properties of feeling mechanical stress. Thus, careful control of parameters is of utmost importance. So far, the most popular method to examine the sensibility of MS channel is patch clamp technique [3, 4]. However, patch clamp is not a so precise way, the pressure exerted on cells membrane is usually between 10 mmHg (1330 pa) and 20 mmHg (2660 pa), which is much bigger than the pressure that MS channel needed for activating.

In our project, we successfully activated two MS channels (Piezo, TRPC5) at 0.01 pa by using microfluidics chip, which is almost corresponding to the proof in some papers that the stress needed to activate some MS channels is less than 1 pa [5, 6]. Here the microfluidics we designed is used for quantitative and precise measurement of the MS channel response in a stable and flexible fashion. Besides, we applied Particle Image Velocimetry (PIV) and computer vision in our microfluidics study. It finally turned out that our measurement’s results perfectly matched our simulations.

Microfluidics design

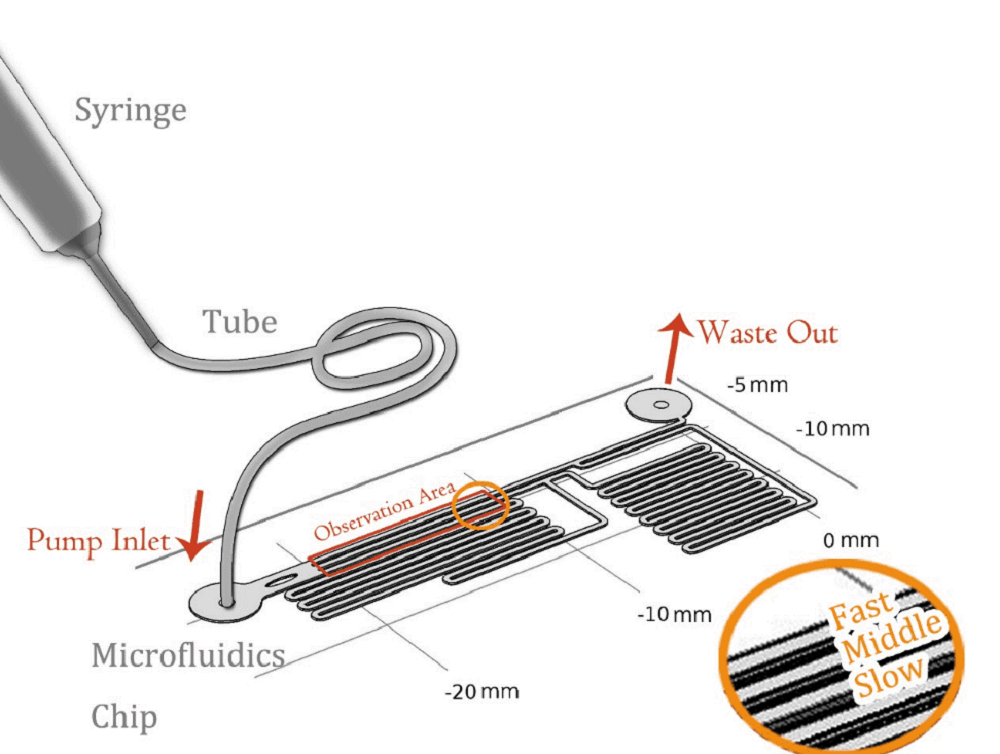
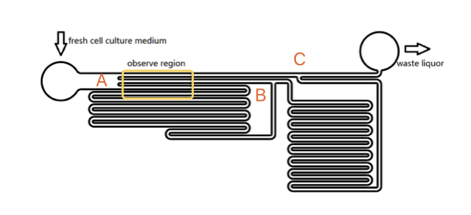
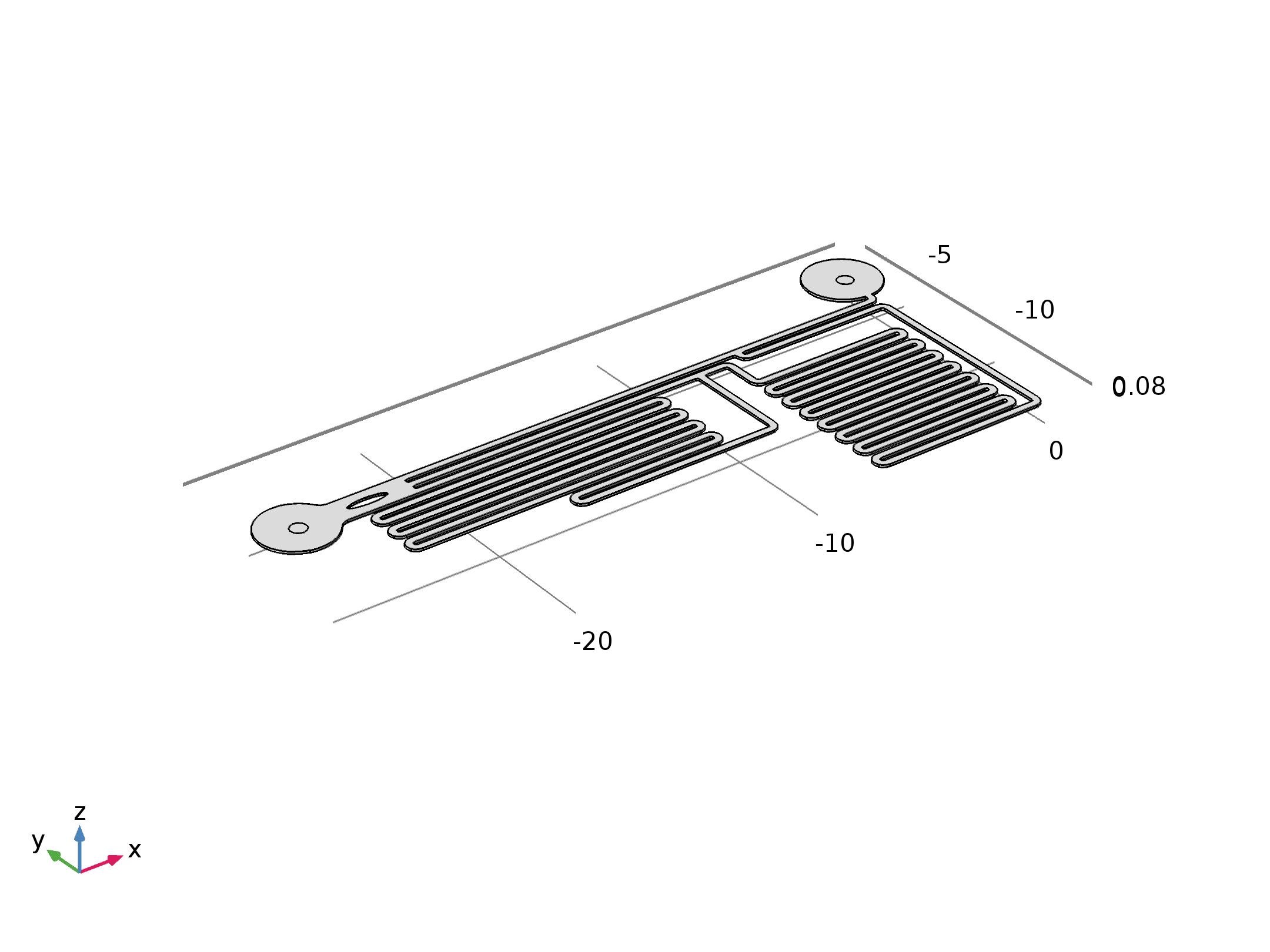
Our experiment was conducted by using microfluidic chip (Fig. 1)(The concept map is as below). CHO-K1 cells were cultured on the surface of glass at the bottom of PDMS tunnel. After liquid passed through, a stable force field could be formed. By controlling the pumped-inflow rate, we could also directly determine the properties of the force field(e.g. Intensity). Each time we applied a constant pumped inflow, cells in 3 different observation tunnel (0.285mm of width, 0.090mm of height) could receive corresponding force of 3 levels---small, middle, large(1: 9: 81). By changing the pumped flow rate, we could measure MS channel’s response under a series of forces and 3 levels magnitudes at a time.

Fig. 1 Microfludic Channels Concept Map

Mathematical demonstration

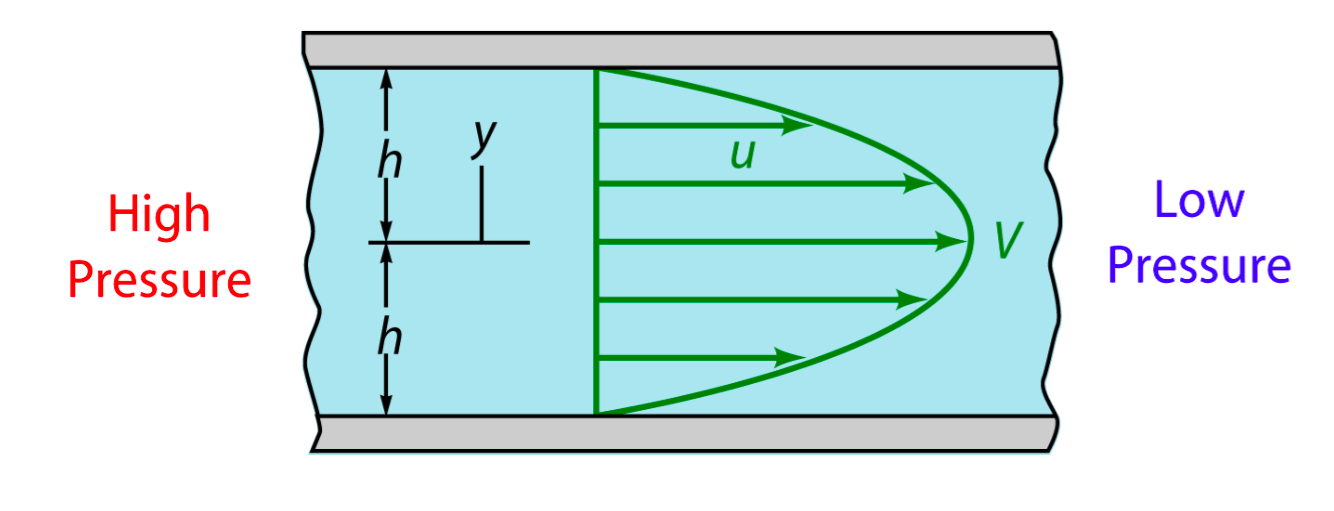
In experiment, when fluid(culture medium x flowed through the tunnel, the shear force was applied on the wall. Seeing the culture medium as a Newtonian flow, it has a constant viscosity μ,0.012dyn·s/cm². The shear stress that medium generated on the wall is proportional to strain rate. As a result, we could relate the magnitude of stress to the velocity gradient along the transversal surface of each tunnel.

Due to the extremely small scale of microfluidic tunnel (only 0.285mm of width and 0.090mm of height), fluid in it observes the Laminar flow. We could assume there is no turbulence when inflow applied constantly, even at the corners, and the head loss of the pumped inflow could also be ignored. The modeling of flow between 2 parallel plates applies to such stable state, in which the magnitude of shear stress on the bottom is proportional to the maximum velocity( at the longitudinal central line).

As the shear stress is proved proportional to the flow rate in the tunnel, we designed the chip to achieve that each of 3 tunnels in observation area has the same transversal surface but the gradient (81: 9: 1 from up to bottom) flow rate, also the average speed.
The lengths of straight tunnels between AB and AC (L_AB, L_AC)are 14.3mm and 12.0mm, and the curved tunnels between AB and BC(R_AB, R_BC) are 108.0 mm and 105.0mm.

Fig. 2 Speed Distribution Inside Channels

Newtonian fluid flows between two wide, parallel plates Flow driven by pressure difference Parabolic velocity profile given by u = V[1-(y/h)^2] where V is the maximum velocity (along channel centerline y=0) Along bottom wall, y=-h, shear stress \tau=\mu \frac{du}{dy}=\mu(-2V\frac{y}{h^2})=\frac{2\mu V}{h} For a constant flow rate within the tunnel, the average speed remains same \bar V=\frac{Q}{A}=\frac{\int_A udA}{A}=\frac{1}{2}V

Fig. 3 Microfluidic Channels

Based on the integral form of the continuity equation for an incompressible fluid, during a given time, the sum of flow volume in each branch is equal to the total volume pumped in the whole chamber. According to the Kirchhoff's law, the accumulation of flow speed at the joint point must be zero. It is easy to get the equation that\begin{matrix} L_{AC}V_1=L_{AB}V_2+R_{AB} V_3 \\ V_2:V_3=R_{AB}:L_{AB} \end{matrix}

Consequently, we could reach the conclusion that the maximum velocity, average flow rate and the shear force on the bottom of each tunnel is at a ratio of 81 : 9 : 1. To verify the modeling result, we made calibration in the real microfluidics chip, and the testing result is very close to designing value (about 75 : 8 : 1 of the maximum velocity ratio in each tunnel) and the simulation result ( 80 : 8 : 1).

Calibration

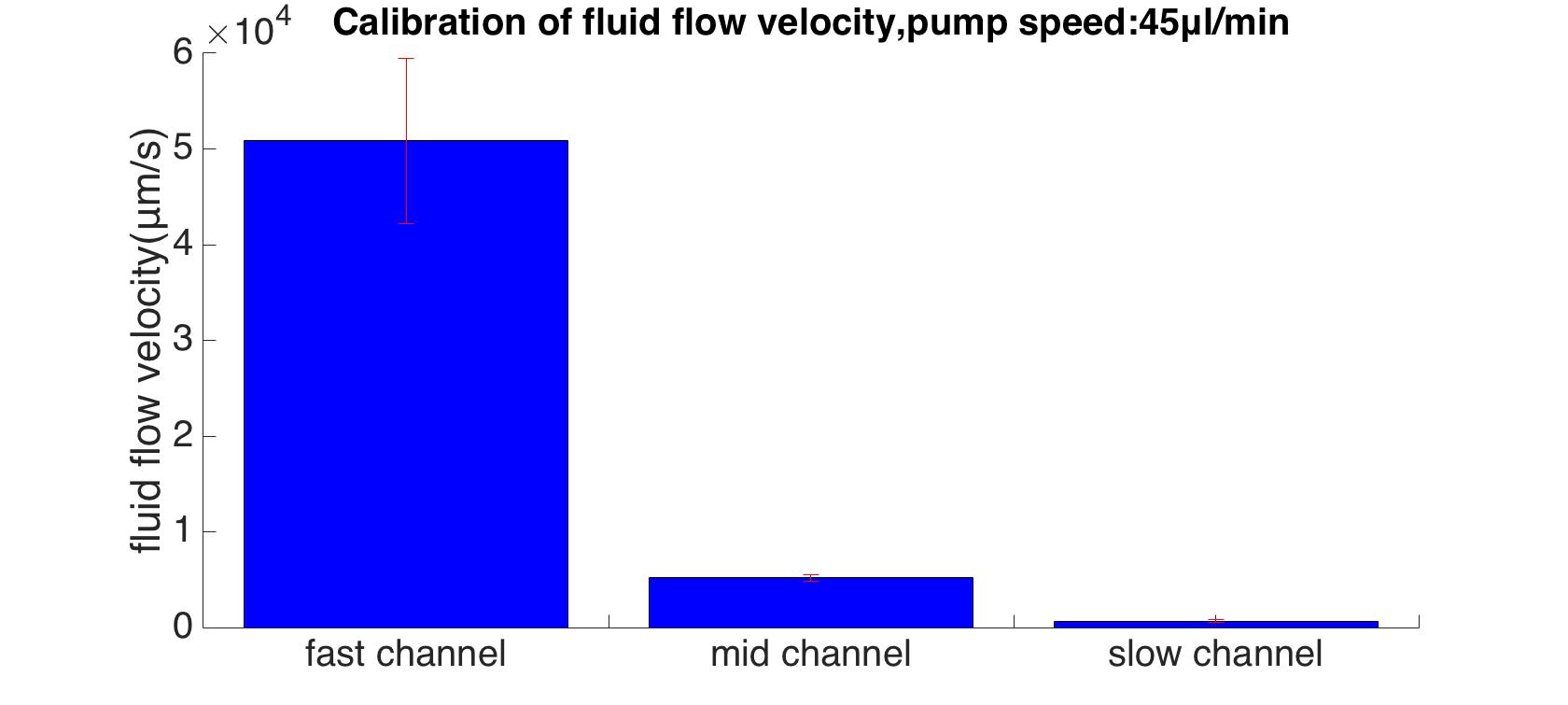
To specify the standard speed of the inflow, Rainbow beads (SPHEROTM Rainbow Calibration Particles, diameter: 6um) were dissolved in the cell culture medium. A series of pumped flow rate (5ul/min, 15ul/min, and 45ul/min) were applied to generate a steady fluid flow. The exposure time was set to 100ms.

Fig.4 Bead Trace in The Fastest Microfluidics Channel with The Flow Rate of 5ul/min

By using MATLAB program, the maximum flow velocities were calculated (13 : 100 : 978).

Fig.5 Maximum Velocities in Each Channel with The Flow Rate of 45ul/min

Code & Details

Simulation

To make the analysis of experimental result convincing, we also made the simulation using the Finite Element Method (FEM) to confirm that the field in microfluidic channel satisfies our expectation. (FEM is a method for modeling and simulating physics-based problems. It divides a large problem into smaller elements, these smaller elements will be solved separately and then be assembled backed to the original model. A collection of smaller elements is called a “mesh”, the “mesh” is constructed by numerous elements, the smaller the size of the element is, the finer the “mesh” is, and the more accurate will the result be). The final geometry set up can be seen from below (Fig.6). [7]

Fig.6 Final Geometry Setup

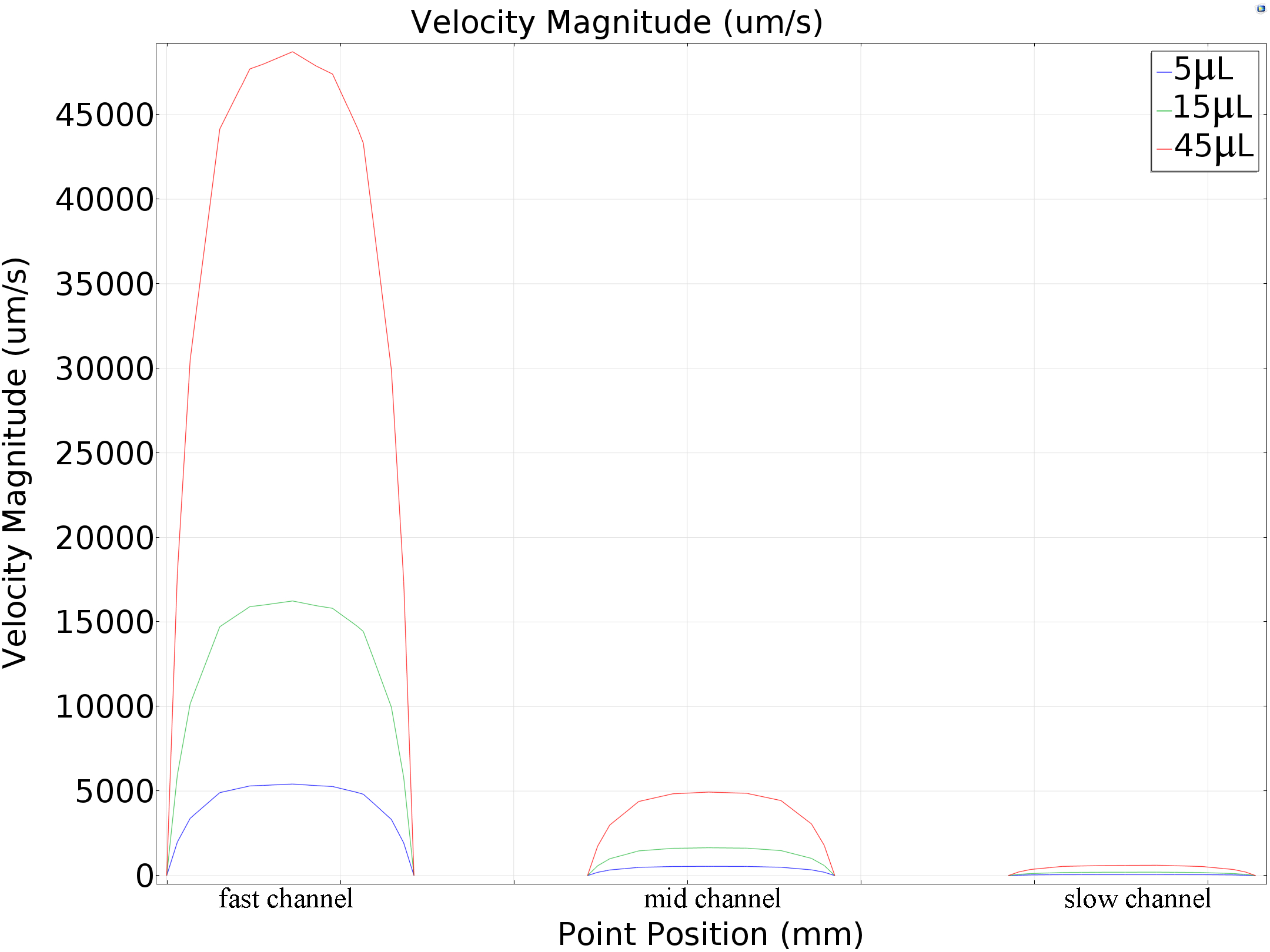
We calculated the velocity magnitude distribution was under different pumped inflow rates (5μL/min, 15μL/min and45μL/min). Results of maximum velocity and shear force that applied on the bottom matched the mathematics perfectly (around 80: 10: 1 in all the conditions, shown in the table below Fig.7).

Fig.7 Velocity Magnitude Distribution on The Cut Line

Channel Flow Rate	fast	middle	slow
5μL/min	5413.994μm/s	548.52153μm/s	67.9229μm/s
15μL/min	16241.73779μm/s	1645.63652μm/s	203.79536μm/s
45μL/min	48723.94763μm/s	4937.93255μm/s	611.65866μm/s

Table 1 Simulation Results of Central Line Speed of each channel

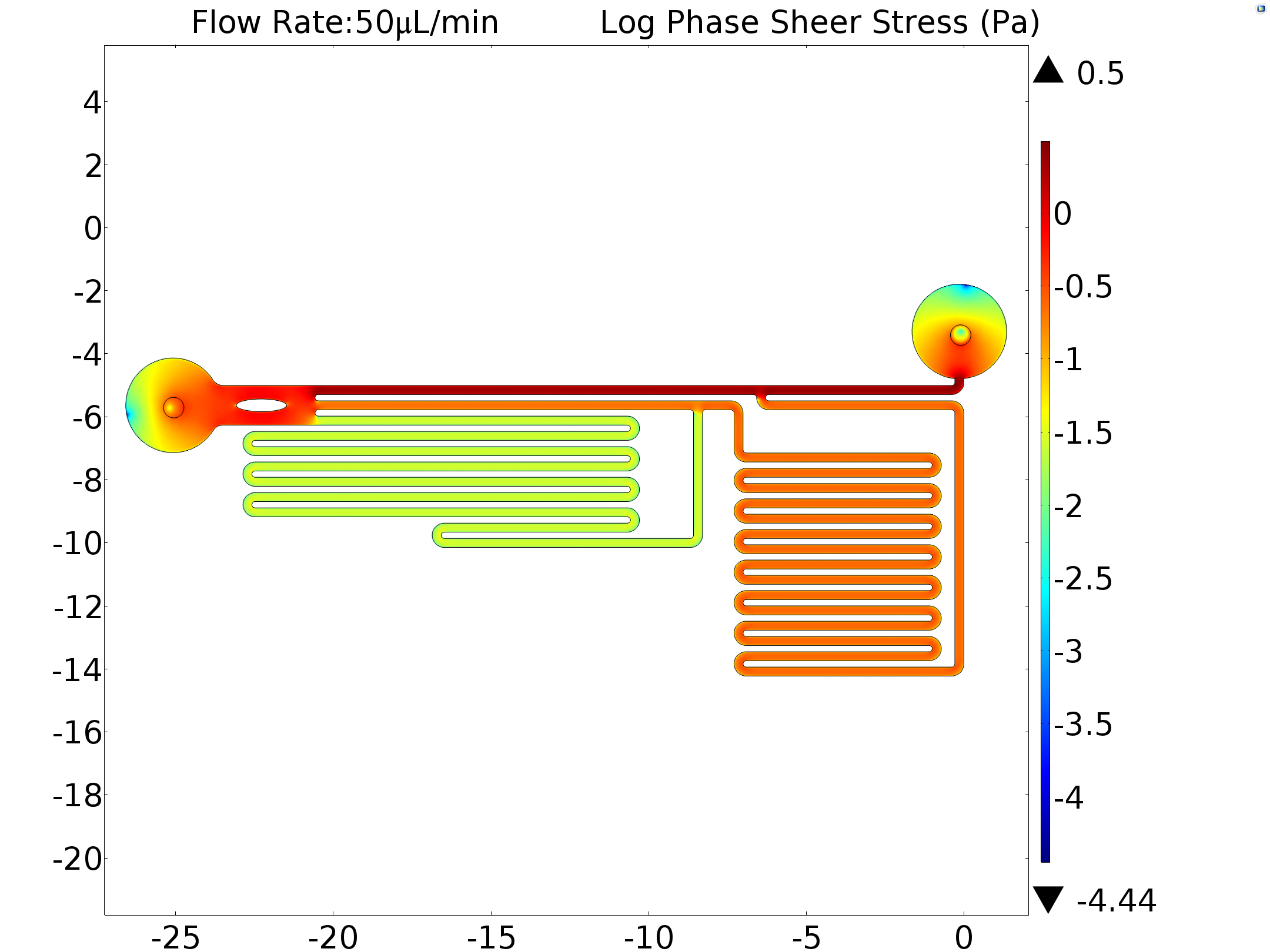
Results of mathematical demonstration (1: 9: 81), calibration (13: 100: 978) and simulation (1: 10: 80) are consistent with each other. This shows that the model is feasible for estimating the shear force that generated by microfluidics on cell membrane. In order to obtain the exact shear force, we inputted the experimentally used flow rate as a boundary condition (6.25μL/min,50μL/min) in our model. The shear stress was also calculated.

Channel Flow Rate	fast	middle	slow
6.25μL/min	1.07519Pa	0.10819Pa	0.0033Pa
50μL/min	2.15057Pa	0.21642Pa	0.02641Pa

Table 2 Simulation Results of Central Line shear Stress

Fig.8 shear Stress Distribution Under Input Flow Rate 50μL/min (log scale)

Detailed Protocol

Data Analysis Method And Software

Because most MS channels are permeable for calcium ion after activated, here we used a calcium indicator, R-GECO, to real-time and quantitatively measure intracellular calcium level. R-GECO is an artificial calcium indicator derived from GCaMP. After binding with calcium, it will emit red fluorescence at around 600nm [8]. Living cell imaging system (Nikon eclipse Ti) was used for time lapse recording the R-GECO fluorescence change when shear stress was applied on cells in microfluidics chips.

We chose five groups of cells in each observation tunnel (fast, mid and slow) and traced the changes of their mean fluorescence intensities of pixels over time. To avoid background noise exists in images, we also chose a region with no cell as noise region to normalize its fluorescence intensity to 0 for each image. In order to accurately and intuitively compare the fluorescence values changing over time, we normalized fluorescence intensity at the start of the recording to 0. Thus, we showed our data in the form of ΔF/F0. (ΔF: Increasing fluorescence value that relative to F0; F0: fluorescence value in the start)

Result and interpretation

We obtained fluorescence images for Piezo1 channel, Piezo1 is a functionally diverse mechanosensitive cation channel. It plays significant role in multiple physiological processes, including sensing shear stress of blood flow for proper blood vessel development, regulating red blood cell functions and controlling cell migration as well as differentiation. [9]

With the increasing importance of Mechanical sensing ion in pathology (many diseases are associated with them, including cardiac arrhythmia (such as atrial fibrillation)[10] cardiac hypertrophy, Duchenne muscular dystrophy, and other cardiovascular diseases[11]), there may be more and more researches that focus on it in the future. We hope that this preliminary exploration with quantitative measurement of MS channel’s sensibility will give people a better understand in the functions and mechanisms of it.

References

Made by from the iGEM team SUSTech_Shenzhen.

Licensed under CC BY 4.0.

• ©2016 SUSTech_Shenzhen