Heterogenous Degradation By PETase
Model Overview
In our experiment we use engineered bacteria as machines to secrete PETase to degrade PET.At first the bacteria secrete PETase ,and then enzymes diffuse into liquid phase body from the cell surface ,from liquid to the surface of PET successively.PETase adsorbs on PET during which process the substrate binding sites of PETase contact with the surface.Finally PETase finds catalytic sites on plastics and combine them with its active center.Ester bonds are broken and chains in PET are ruptured,resulting in the degradation of PET.
Assumptions
1. There exists feedback inhibition regulation in the growing process of a single bacteria. Unlimited growth of population growth can’t be supported due to the limitation of space and resources in a certain environment. When the population of individual bacterium has too much increased, the environment degrades and the average resource share declines, resulting in reduction in birth rate while mortality rate is increasing. Consequently it is reasonable to assume that there exists feedback inhibition regulation due to the influence of environmental factors.
2. A cell can be roughly considered as a sphere.
3. Enzymes are in the dynamic equilibrium when transferring in the liquid phase.
4. The resistance of enzymes’ spread from liquid body to the surface of PET is much larger than that of from the cells’ surroundings to liquid body.
5. It takes several steps for the enzymes to complete the degradation of PET. Enzymes have the substrate binding sites and active centers. We assume that the enzymes are firstly combined with the polymer substrate through their own substrate binding sites, and then the active centers catalyzed the degradation of the polymers.
6. The degradation of PET takes place on the surface of PET.
7. The mass transfer of enzymes in the liquid phase will cause some of them to stay in the liquid body and the delay of enzyme concentration changes on the PET surface.
Summary
Based on the assumptions above and the description of PET degradation process in a heterogeneous system, we first establish the equation of measuring how much percent the PET degrades and how much the degrading rate is. Then we use the simple but mature Logistic Equation to describe the process of cell growth, and Leudeking-Piret Equation which is a correlation between cell growth rate and product producing rate, to describe the kinetic process of PETase production. Then we use the general method of describing mass transfer process to establish mass transfer rate equation when enzymes diffuse from the cell surface to liquid phase body then from liquid phase body to the PET surface, and the distribution equation of enzyme concentration, respectively.
From those equations we can get the total mass transfer rate equation of the enzymes in a heterogeneous system. We analyze and then make a conclusion that the mass transfer diffusion mainly leads to the delay of enzyme concentration change on the PET surface .Finally, taking that MHET, the product of PET degradation, will show competitive inhibition effect into consideration, based on the adsorption equilibrium of PETase on the PET surface, we use the steady state approximation theory and deduce the total kinetic equation of PETase degrading PET. Solve this differential equation we obtain the degradation rate curve of PET under heterogeneous system.
The Formulas for Calculating Biodegradation Percentage and The Degradation Rate
Since our project aims to degrade PET, we need to propose a stable index to measure the degree of degradation of the plastics and another one to measure the degradation rate. Here we choose to describe degradation rate and percentage.
The role of PETase plays in the degradation is to catalyze the cleavage of ester bonds between TPA and EG. This cleavage will directly lead to the decomposition of whole polymer chain and finally the instability of plastics. Thus we choose the ester bond number as an index to evaluate this degradation process.
The calculation formula for calculating the number of moles of ester bonds (namely the number of moles when polymers are completely degraded):
$${n_{EB}} = {n_{EB/{M_{rep}}}} \cdot m/{M_{rep}} $$
| nEB | The mole number of the broken ester bonds in theory(μmol) |
| m | Loading amount of the polymer (μg) |
| Mrep | The molar mass of the repeat units in the polymer(μg/μmol) |
| nEB/Mrep | The number of ester bonds in a repeat unit |
The percentage of degradation of ester bonds can be obtained through that ratio.
$$\omega = {n_{\exp }}/{n_{EB}}$$
Similarly, the degrading rate can also be described by a series of formulas shown below:
$$v = - \frac{{d{n_{\exp }}}}{{dt}}$$
The Equation for The Growth Rate of Enzyme Proteins
The kinetics of cell growth
According to the characterisitics of microbial cell growth, Monod Equation is the most commonly used one. Although this equation is considered to be simple and effective when used to describe the growth of bacteria, it is only suitable under the condition that there is no other restrictive substances in the environment. In our system, PETase is secreted by the bacteria to the environment and, more limitation by feedback regulation will arise if it is in a mixed bacteria system. Thus we utilize the Logistic Equation to describe the rhythm of the growth rate.
Logisic model is a typical S-shaped curve that can reflect the inhibition effect caused by the increase of bacteria concentration in the fermentation process. In the early stage, the bacteria concentration is low , namel cx is much lower than cxm, therefore the item of cx/cxm can be neglected. The colony is in the stationary phase after the logarithmic phase and at that time cx is close to cxm. The colony ceases to grow. The whole process can be described in the following equation:
\[{r_x} = \frac{{d{c_x}}}{{dt}} = {\mu _m}{c_x}(1 - \frac{{{c_x}}}{{{c_x}_m}})\]
| Rx | The growth rate of cell growth |
| Cx | The concentration of cells |
| Cxm | The maximum concentration of cells |
| μ | Specific growth rate , namely the growth rate of a unit thalli concentration |
| μm | The maximum specific growth rate |
The definition of μ is :
$$\mu = \frac{{{r_x}}}{{{c_x}}}$$
When cells are in exponential phase, μ is generally a constant,so
$$\mu = \frac{1}{t}\ln \frac{{{c_x}}}{{{c_{x0}}}}$$
Under the condition when t=0, cx=cx0, we integrate the formula above:
\[{c_x} = \frac{{{c_x}_0{c_x}_m{e^{{\mu _m}t}}}}{{{c_x}_m - {c_x}_0(1 - {e^{{\mu _m}t}})}}\]
Solve this equation and the growth curve can be obtained:
The formation dynamics of expression product (PETase)
The extreme diversity of metabolites produced by microbial fermentation and the complexity of biosynthesis routes in the cells cause the biosynthetic pathways and metabolic regulation mechanism of those metabolites to show diverse characterisitics. We use the relations between cell growth rate and the production rate to describe the rate of protein production. The universal model can be expressed by Leudeking-Piret Equation:
\[{r_E} = \frac{{dE}}{{dt}} = \alpha \frac{{d{c_x}}}{{dt}} + \beta {c_x}\]
| α | A product synthesis constant associated with bacteria growth(g•g-1) |
| β | A product synthesis constant irrelevant with bacteria growth(g•g-1•h-1) |
When α≠0 and β=0, the model is growth coupling. When α=0 and β≠0, the model is non-growth coupling. When α≠0 and β≠0, the model is partial-growth coupling.
Plug the cell growth rate into the equation to simplify:
\[{r_E} = \frac{{dE}}{{dt}} = {c_x} \cdot \left[ {\alpha {\mu _m}(1 - \frac{{{c_x}}}{{{c_{xm}}}}) + \beta } \right]\]
Integrate the equation above.
\[E = \alpha (\frac{{{c_{x0}}{c_m}{e^{{\mu _m}t}}}}{{{c_m} - {c_{x0}} + {c_{x0}}{e^{{\mu _m}t}}}} - {c_{x0}}) + \frac{{\beta {c_{xm}}}}{{{\mu _{xm}}}}\ln \frac{{{c_{xm}} - {c_{x0}} + {c_{x0}}{e^{{\mu _m}t}}}}{{{c_{xm}}}}\]
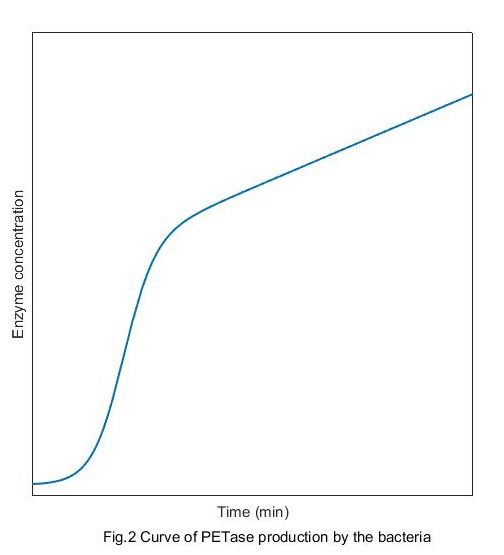
Solve this equation and the production curve of PETase can be obtained:
Compared with the growth curve of bacteria, we can see intuitively that at the beginning, the correlation between the enzymes production and the concentration of bacteria is high. And with the time passing by the correlation becomes lower and finally disappears.
The Transfer Process of Enzymes in The Liquid Phase
The secretion of enzymes from cells will inevitably lead to the increase of enzyme concentration nearby. And when enzyme concentrations surrounding the cells are larger than that in the liquid phase body, a driving force will emerge, causing the diffusion of enzymes into liquid phase body. On the other hand, the enzymes in the liquid phase will reach the surface of PET along with the free diffusion of molecules. So there are two transfer processes before the enzymes adsorp on the PET surface.
The mass transfer process of enzymes in the liquid phase body
Cells secrete enzymes to the outside. Here a cell can be regarded as a sphere and there’s a spherical shell composed by the enzymes in the outer surface of the sphere. Inside this shell an unsteady mass transfer process will occur along the radius direction.
Do differential enzyme E mass balance in a sphere with radius r and thickness dr. The rate of mass imported from the inner surface:
$${r_{imp}}{\rm{ = }}{j_{{\rm{er}}}} \cdot 4\pi {r^2}$$
| rimp | Rate of imported mass |
The rate of mass output from the outside surface is:
$${r_{\exp }}{\rm{ = }}{j_{{\rm{er}}}} \cdot 4\pi {r^2}{\rm{ + }}\frac{{\partial ({j_{{\rm{er}}}} \cdot 4\pi {r^2})}}{{\partial r}}dr$$
| rexp | Rate of exported mass |
The rate of mass accumulation in the sphere:
$${r_{acc}}{\rm{ = }}\frac{{\partial E}}{{\partial t}} \cdot 4\pi {r^2}dr$$ $${r_{pro}}{\rm{ = }}{r_E} = \frac{{dE}}{{dt}}$$
| racc | Rate of accumulation |
| rpro | Rate of production |
Based on the conservation of mass, we can get:
Rate of exported mass – rate of imported mass + rate of accumulation – producing rate = 0
Substitute those rate of mass into this equation:
$$\frac{{\partial ({j_{er}}{r^2})}}{{\partial r}} + \frac{{\partial E}}{{\partial t}}{r^2} - {R_E} = 0$$
Based on Fick’s first law,
$${j_{er}} = - D\frac{{\partial E}}{{\partial r}}$$
Substitute and sort this equation. Finally, we can get the unstable diffusion differential equation while the enzymes near the cells are secreted along direction r.
$$\frac{{\partial E}}{{\partial t}} = D\frac{1}{{{r^2}}}\frac{\partial }{{\partial r}}({r^2}\frac{{\partial E}}{{\partial r}}) + {r_E}$$
Integrate the equation above then we can get the distribution equation of the enzyme concentration.
If we use the diffusion rate equation, the rate of enzyme diffusion from cells to liquid phase body can be described as:
\[\frac{{d{E_x}}}{{dt}} = {k_c}{a_c}({E_c} - {E_x})\]
| Ex | The concentration of enzyme in liquid phase body |
| Ec | The concentration of enzyme on cell surface |
| kc | Mass transfer coefficient in liquid phase |
| ac | The surface area of cells |
Mass transfer process of enzymes from liquid phase to the surface of PET
Similar to the process of diffusion from cells to liquid body, based on Fick’s first law and mass conservation we can get the differential equation of the diffusion process.
$$\frac{{\partial E}}{{\partial t}} = D(\frac{{{\partial ^2}E}}{{\partial {x^2}}} + \frac{{{\partial ^2}E}}{{\partial {y^2}}} + \frac{{{\partial ^2}E}}{{\partial {z^2}}}) + {r_E}$$
If we integrate the formula above, we can get the distributing equation of the enzyme concentration.
Similarly with the diffusion rate equation, the equation of the rate of enzyme diffusion from liquid to PET surface can be obtained:
$$\frac{{d{E_p}}}{{dt}} = {k_p}{a_p}({E_x} - {E_p})$$
| Ex | The enzyme concentration in liquid phase |
| Ep | The enzyme concentration on the cells’surface |
| kp | Mass transfer coefficient in liquid phase |
| ap | The surface area of cells |
Total diffusion rate equation in liquid phase
The total diffusion equation of the process can be described as:
$$\frac{{dE}}{{dt}} = Ka({E_c} - {E_p} - \Delta E)$$
| K | the total mass transfer coefficient |
| a | Solid-liquid interface contact area |
| Ec | the enzyme concentration on cells’surface |
| Ep | the enzyme concentration on PET surface |
| ΔE | The loss of driving force of mass transfer caused by the enzyme concentration accumulation in the liquid phase. |
Assuming that the diffusion process in liquid phase is a dynamic balancing process, which means the concentration variation in the liquid phase body is equal to the rate of enzyme production, it can be describe as:
$$\frac{{d{E_c}}}{{dt}} - {r_E} = \frac{{d{E_P}}}{{dt}}$$
The expanded form is:
\[\frac{{dE}}{{dt}} = \frac{{({E_c} - {E_x}) - \frac{{{r_E}}}{{{k_c}{a_c}}} + ({E_x} - {E_p})}}{{\frac{1}{{{k_c}{a_c}}} + \frac{1}{{{k_p}{a_p}}}}}\]
So the relationship between the parameters in total mass flux equation and those in interphase mass flux equation is:
$$\frac{1}{{Ka}} = \frac{1}{{{k_c}{a_c}}} + \frac{1}{{{k_p}{a_p}}}$$
\[\Delta E = \frac{{{r_E}}}{{{k_c}{a_c}}}\]
As we can see, the total resistance for enzymes in liquid phase is the resistance from cell surface to liquid phase body plus that from liquid to PET surface. In this system, the adsorption of enzymes on the PET surface will lead to the accumulation of the enzymes. So the concentration gradient drops in the concentration field near the PET surface. As a result, the most of the resistance for enzyme transfer in liquid phase is that from liquid to PET surface, which can be described as:
\[\frac{1}{{Ka}} = \frac{1}{{{k_c}{a_c}}}\;\;\;\;\;K \approx \frac{{{k_c}{a_c}}}{a}\]
Time loss caused by mass transfer in liquid phase
After secreted by cells, enzymes diffuse to the surface of PET through liquid phase.In the process of mass tranfer, enzyme concentration in liquid phase will be balanced with that on the surface of cells and that on the surface of PET.Thus some enzymes will remain in liquid phase body.And the mass transfer process will lead to the delay of enzyme concentration change on the PET surface.This can be expressed by the equation below:
\[\int_t^{t + T} {Ka({E_c} - {E_P} - \Delta E)dt = {E_c} - {E_P}} \]
| T | Delay time,a function of time |
The equation above is an integral equation.Corresponding differential equation is:
\[Ka[\frac{{dT}}{{dt}}\Delta E(t + T) - \Delta E(t)] = \frac{{\Delta E(t)}}{{dt}}\]
Intergrate this equation and we get the relation between delay time T and time:
The process of PETase adsorbing on PET surface and enzymes catalyzing PET degradation
The biodegradation of polymer by enzymes is a kind of heterogeneous enzymatic reactions. Since the classical dynamics equation for enzymatic reaction, Michaelis-Menten equation, is based on homogeneous enzyme- substrate system, it’s not suitable to describe the process of the degradation of polymers. Enzymes will act with polymers through their bonding sites and combine with the substrate after their secretion and diffusion to the PET surface from cells. Both of the molecular configurations change after the adsorption. The enzymatic active center will expose to ‘find’ the corresponding sites on the polymer. At the same time, the polymer must offer the active segment. Then the enzymes catalyze to break the ester bonds, and the small molecules such as MHET will be released and diffuse into the liquid phase. Finally PET will desorb enzymes.
Establishment of dynamics equation for PET enzymatic degradation
Assuming that there is a bonding site and an active center in the enzyme, it combines with the substrate through its bonding site and then degrades the polymer with its active site. In this system the product molecules still contain ester bonds, as a result, MHET may act with the enzymes before its diffusion into the solution and restrain the combination between PET and PETase. This competitive restraint will lead to a declination in the catalysis rate. Those above can be described as:

Compared with other kinds of plastics, PET is more difficult to be degraded for the sake of its distinct structure. Aliphatic polymers are biodegradable for its good elasticity while aromatic polymer is rigid with benzene. Through the above description of the process, the enzyme need to find an active segment to combine with. So it supposes the polymer to get flexibility to increase the possibility to react with PETase. However, the rigidity of PET leads to reducing of the activity of PETase. So this step is the restrict step of the whole enzymatic process. Based on the stationary approximate theory, we can get the total dynamics equation.
Dynamics equation of enzyme absorption
The fraction of coverage can be described as:
\[\theta = \frac{A}{{{A_0}}} = \frac{{{q_E}}}{{{q_{{E_{\max }}}}}}\]
| θ | The fraction of coverage by enzyme on the polymer surface |
| A0 | The total mass transfer coefficient |
| A | Area already covered |
| qE | The content of absorption for enzyme per area on polymer |
| qEmax | The maximum absorption amount |
Because enzymatic catalytic step is a rete controlling step, the absorption on polymer surface is a dynamic balancing process.
Rate of absorption:\[{r_1} = d[ES]/dt = {k_1}[E](1 - \theta )\;\]
Rate of desorption:\[{r_2} = d[E]/dt = {k_{ - 1}}\theta \]
From r1=r-1, we can get: k1[E] (1-θ) = k-1θ. Combining with the fraction of coverage we can get:
\[\theta = \frac{{{q_E}}}{{{q_{{E_{\max }}}}}} = \frac{{{K_A}[E]}}{{1 + {K_A}[E]}}\]
| [E] | The concentration of enzyme] |
| KA | Absorption balancing constant |
The above equation is Langmuir equation
Establishment of equation for rate of total degradation of PET
After absorption to the surface, the combination and escape is a dynastic balancing process because of the competitive substrate.
\[{k_3}[ES][P] = {k_{ - 3}}[ESP]\]
| [ES] | The concentration of enzyme absorbed |
| [P] | The concentration of MHET |
| [ESP] | The concentration of enzyme combined with MHET |
\[[ESP] = {K_B}[ES][P]\]
| KB | Constant of substrate restraint balance |
The enzymatic degradation is interfacial reaction before degradation in large scale. So the rate of degradation of polymer, the absorbed enzyme amount, the inactive combined enzyme mount, the density of ester bond on polymer surface and the superficial area have the following relation:
\[v = - \frac{{d{n_{\exp }}}}{{dt}} = A \cdot {k_2} \cdot {\rho _{EB}}({q_E}A - {n_E})\]
| v | The rate of degradation[mol/min] |
| t | Time[min] |
| k2 | Constant of degradation rate [cm3/(min•mg)] |
| A | Superficial of polymer[cm2] |
| nE | The inactive combined enzyme mount[mol] |
Connecting with the absorption balance and the substrate restrain balance, we can get the total rate of degradation equation:
\[v = {k_2}{\rho _{EB}}(\frac{{{K_A}[E]{q_{{E_{\max }}}}A}}{{1 + {K_A}[E]}} - {K_A}{K_B}{[E]^2}[P] \cdot V)\]
| V | The volume of the system |
With mass conservation, we can get:
\[{E_p} = E + ES + ESP\] \[[E] = \frac{{[{E_P}]}}{{1 + {K_A} + {K_A}{K_B}[P]}}\]
| [Ep] | The concentration of enzymes on the plastic surface |
Because the concentration of enzyme is low in the system and the producing rate of MHET is equal to the rate of PET degradation, we can get the following formula:
\[\theta = {K_A}[E]\] \[\, - \frac{{d{n_{\exp }}}}{{dt}} = \frac{{Vd[P]}}{{dt}}\]
Considering that MHET in substrate restrain is easy to diffuse to liquid, which means the balance is small, we can get the final equation for plastic degradation:
\[v = \frac{{d[P]}}{{dt}} = \frac{{{k_2}{\rho _{EB}}}}{V}(\frac{{{K_A}[EP]{q_{{E_{\max }}}}A}}{{1 + {K_A} + {K_A}{K_B}[P]}} - \frac{{{K_A}{K_B}{{[{E_P}]}^2}[P]}}{{{{(1 + {K_A})}^2}}})\]
The above equation is differential whose only variable is the concentrate of MHET. So we can transform the equation as the following form:
\[\frac{{d[P]}}{{dt}} = \frac{a}{{[P]}} - b[P]\]
Both a and b here are constants.
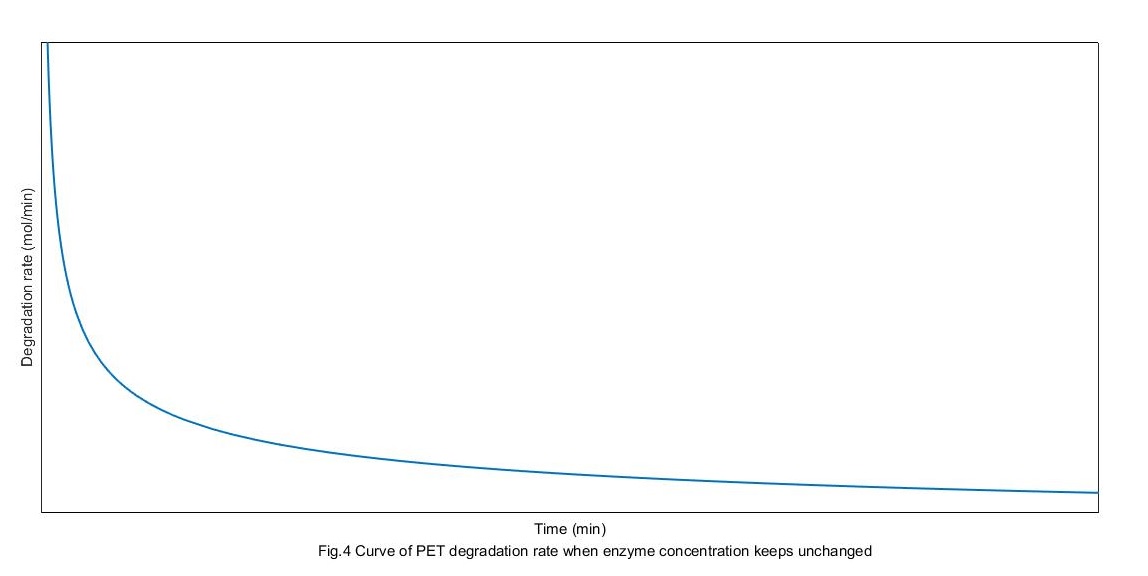
The concentration of MHET is 0 initially. Solve the above differential equation, we can get the curves of the rate of PET degradation as following:
From the above figure, enzymes get to the absorption balance and get the biggest rate of degradation. But the rate get down gradually with substrate restrain.
Solution of PET Degradation Rate Considering The Whole System
Solution of PET degradation rate considering the process of cells secrete protein
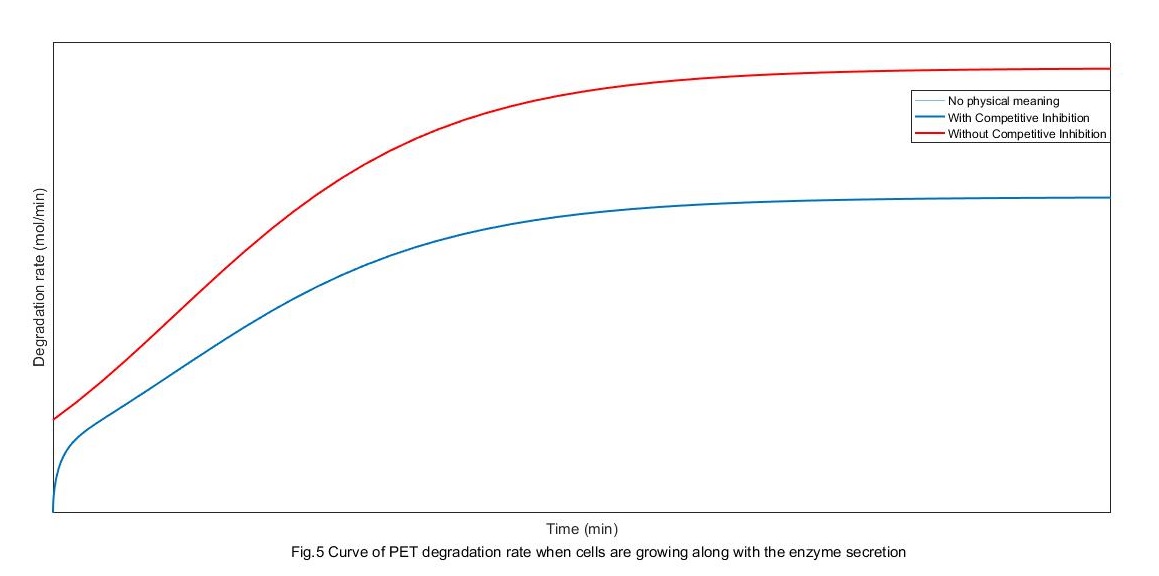
We have got the rate of enzyme production by connecting with the growth process of cells before. Substitute it into the total equation of PET degradation rate then we can get the rate of PET degradation with cells. Marge constants:
\[v = \frac{{c[{E_P}]}}{{d + e[P]}} - f{[{E_P}]^2}[P]\] \[v = g[{E_P}] - h{[{E_P}]^2}\]
c,d,e,f,g,h here are constants.
From the above figure, the rate of degradation without competitive restrain is pretty lower than it with competitive restrain. When there is competitive restrain, the change of degradation rate can be divided into three stages. First, the absorption controlling stage at which the absorption amount of enzyme increases with its secretion. Second, the secretion controlling stage at which the secretion rate gets to saturation because of the saturation of cell growth. Finally, PET degradation rate settle out because of both the two factor, mostly because the absorption gets its saturation.
Rate of the whole process for cells to secrete and degrade in heterogeneous phase
We just calculated the enzymatic degradation rate while ignored the transmission in the liquid. The transmission will lead to loss of the effective enzyme and latency of arrival for enzyme to PET surface. Connecting these two factor with the above total equation and substitute constants we can get:
\[v = \frac{{c[EP](t - T)}}{{d + e[P](t)}} - f{([EP](t - T))^2}[P](t)\]
| [Ep](t-T) | The concentration on PET surface is a function of time t-T |
| [P](t) | The concentration of MHET is a function of time t] |
Solve the above equation, then we get the curves of PET degradation rate in heterogeneous phase.
From the figure above , the change of degradation rate can be divided into three stages no matter if there is liquid transmission. And the liquid transmission effect the second stage most, at which cells grow up and secret more. The liquid transmission effect less on absorption controlling stage and saturation stage. That can be reasonable because absorption is just related to the concentration of enzyme on the PET surface. And enzymes secreted by cells can only get to plastic surface through liquid transmission in secretion controlling stage.
Conclusion and Prospect
We begin to build our models above from the process analysis of PET degradation in heterogeneous system. We construct models for each step and finally deduce the rate curve of PET degradation by the enzymes secreted by bacteria in heterogeneous system.From this curve we can see that the degradation can be devided into 3 parts.In the first part, degradation rate is under the control of bacteria growth and enzyme secretion.In the second part, it is controlled by the mass transfer of enzyme in the liquid phase.In the third part, it is controlled by the catalytic ability of enzymes adsorbed on the PET surface .From the trend of the curve we can conclude that, in order to degrade PET with a higher rate or make the rate peak as soon as possible,what we first need to do is to promote the growth of bacteria.This will enhance the enzyme concentration.On the other hand, we can accelerate the diffusion of enzymes in the liquid phase.For example,shake cultivation or stirred culture,can eliminate the influence of time delay and make the degradation rate reach the peak fast.Our system assumes that PET degradation only takes place on the surface of PET.Although it's reasonable,as the degradation proceeds, small gaps will form on the plastics due to degradation.If they become so large that enzymes can diffuse into the interior of PET,degradation process will be accelerated to a huge extent.The next step of building models is to take the process and threshold value of internal diffusion into consideration.This will provide a more accurate model to describe the process of PET degradation in the heterogeneous system.
Refenerce
[1] Ma Mengmeng. Studies on Enzymatic Degradation of Polymer Nanoparticles and Adsorption Mechanism of Enzymes on Nanoparticles [D]. Tianjin: School of Chemical Engineering and Technology,Tianjin University,2004
[2] Liu Bin. High-density Fermentation of Genetically Engineered Pichia pastoris Expressing Recombinant Human-source Collagen [D]. Nanjing: Nanjing University of Science & Technology,2012
[3] Chen Li, Wang Yue, Guo Meijin,et al.Kinetic modelling of porcine insulin precursor (PIP) expressed by multi-copy recombinant Pichia pastoris [J]. CIESC Journal, 2016, 67(5):2015-2021
[4] Chen Tao, Zhang Guoliang. Chemical transfer process foundation[M]. Beijing: Chemical Industry Press,2009
[5] Jia Shaoyi, Chai Chengjing. Chemical mass transfer and separation process[M].Beijing: Chemical Industry Press,2007
[6] Tan Tianwei. Biochemical Engineering[M].Beijing: Chemical Industry Press,2008
[7] Li Songlin, Zhou Yaping, Liu Junji.Physical chemistry[M]. Higher Education Press, 2009
[8] Li Shaofen.Chemical Reaction Engineering[M]. Beijing: Chemical Industry Press,2012