| Line 1: | Line 1: | ||
<html><head> | <html><head> | ||
| − | <meta charset="utf-8"><link rel="shortcut icon" href="/wiki/images/8/80/T--NCKU_Tainan--favicon.png" type="image/x-icon"><link rel="icon" type="image/png" href="/wiki/images/8/80/T--NCKU_Tainan--favicon.png"><link rel="icon" type="image/x-icon" href="/wiki/images/8/80/T--NCKU_Tainan--favicon.png"><meta name="viewport" content="width=device-width, initial-scale=1.0"><meta property="og:title" content="Project Modeling : Statistics Analysis - iGEM NCKU"><meta property="og:site_name" content="Project Modeling : Statistics Analysis - iGEM NCKU"><meta property="og:description" content=""><title>Project Modeling : Statistics Analysis - iGEM NCKU</title><meta http-equiv="Content-Type" content="text/html" charset="utf-8"><meta property="og:image" content=""><meta property="og:image:type" content="image/png"><link rel="stylesheet" href="/Team:NCKU_Tainan/css/frame/T--NCKU_Tainan--bootstrap_min_css?ctype=text/css&action=raw"><link href="/Team:NCKU_Tainan/font/T--NCKU_Tainan--NotoSans_css?ctype=text/css&action=raw" rel="stylesheet" type="text/css"><link rel="stylesheet" href="/Team:NCKU_Tainan/font/T--NCKU_Tainan--font-awesome_min_css?ctype=text/css&action=raw"> | + | <meta charset="utf-8"><link rel="shortcut icon" href="/wiki/images/8/80/T--NCKU_Tainan--favicon.png" type="image/x-icon"><link rel="icon" type="image/png" href="/wiki/images/8/80/T--NCKU_Tainan--favicon.png"><link rel="icon" type="image/x-icon" href="/wiki/images/8/80/T--NCKU_Tainan--favicon.png"><meta name="viewport" content="width=device-width, initial-scale=1.0"><meta property="og:title" content="Project Modeling : Statistics Analysis - iGEM NCKU"><meta property="og:site_name" content="Project Modeling : Statistics Analysis - iGEM NCKU"><meta property="og:description" content=""><title>Project Modeling : Statistics Analysis - iGEM NCKU</title><meta http-equiv="Content-Type" content="text/html" charset="utf-8"><meta property="og:image" content=""><meta property="og:image:type" content="image/png"><link rel="stylesheet" href="/Team:NCKU_Tainan/css/frame/T--NCKU_Tainan--bootstrap_min_css?ctype=text/css&action=raw"><link href="/Team:NCKU_Tainan/font/T--NCKU_Tainan--NotoSans_css?ctype=text/css&action=raw" rel="stylesheet" type="text/css"><link rel="stylesheet" href="/Team:NCKU_Tainan/font/T--NCKU_Tainan--font-awesome_min_css?ctype=text/css&action=raw"> <link rel="stylesheet" href="/Team:NCKU_Tainan/css/frame/T--NCKU_Tainan--hljs_github_css?ctype=text/css&action=raw"> |
| + | <link rel="stylesheet" href="/Team:NCKU_Tainan/css/T--NCKU_Tainan--Model_css?ctype=text/css&action=raw"> | ||
</head> | </head> | ||
<body> | <body> | ||
| Line 12: | Line 13: | ||
<div class="head2">Model: Statistics Analysis</div> | <div class="head2">Model: Statistics Analysis</div> | ||
<div class="title-line" id="intro">Introduction</div> | <div class="title-line" id="intro">Introduction</div> | ||
| − | <p>In medicine, the blood glucose exceeding 5mM/L implies having diabetes, and it exceeding 120mM/L implies being a severe patient. Finding the person whose glucose concentration is over 5mM/L or 120mM/L is our target. First, we prove that there has difference between 0.1mM/L and 5mM/L (120mM/L) in the <a href="#pair" onclick="toEvent('pair');">paired-difference T test</a> part. And, we use the <a href="#reg" onclick="toEvent('reg');">regression and prediction intervals</a> to distinguish exceeding 120mM/L and 5mM/L from exceeding 0.1mM/L. From the result, 5mM/L can be distinguished from 0.1mM/L after 101 minutes, and 120mM/L can be distinguished from 0.1mM/L after 88 minutes.</p> | + | <p>In medicine, the blood glucose exceeding 5mM/L implies having diabetes, and it exceeding 120mM/L implies being a severe patient. Finding the person whose glucose concentration is over 5mM/L or 120mM/L is our target. First, we prove that there has difference between 0.1mM/L and 5mM/L (120mM/L) in the <a href="#pair" onclick="return toEvent('pair');">paired-difference T test</a> part. And, we use the <a href="#reg" onclick="return toEvent('reg');">regression and prediction intervals</a> to distinguish exceeding 120mM/L and 5mM/L from exceeding 0.1mM/L. From the result, 5mM/L can be distinguished from 0.1mM/L after 101 minutes, and 120mM/L can be distinguished from 0.1mM/L after 88 minutes.</p> |
<img src="/wiki/images/c/c0/T--NCKU_Tainan--project-modeling-statistic-image1.jpg"> | <img src="/wiki/images/c/c0/T--NCKU_Tainan--project-modeling-statistic-image1.jpg"> | ||
<img src="/wiki/images/0/04/T--NCKU_Tainan--project-modeling-statistic-image2.jpg"> | <img src="/wiki/images/0/04/T--NCKU_Tainan--project-modeling-statistic-image2.jpg"> | ||
| Line 202: | Line 203: | ||
sd<-var^0.5 | sd<-var^0.5 | ||
t<-(dbar/sd)*(11^0.5)</code></pre> | t<-(dbar/sd)*(11^0.5)</code></pre> | ||
| − | <div class="title-line" id="reg | + | <div class="title-line long" id="reg"></div> |
| − | <div | + | <div class="title-content">Regression & Prediction interval</div> |
<p> Our product uses the fluorescence intensity to obtain the concentration of blood glucose. Therefore, whether we could precisely distinguish exceeding 120mM/L and 5mM/L from exceeding 0.1mM/L becomes the most important problem. We use the skill of the prediction interval in this part.</p> | <p> Our product uses the fluorescence intensity to obtain the concentration of blood glucose. Therefore, whether we could precisely distinguish exceeding 120mM/L and 5mM/L from exceeding 0.1mM/L becomes the most important problem. We use the skill of the prediction interval in this part.</p> | ||
<br> | <br> | ||
| Line 309: | Line 310: | ||
<div class="col-md-3"> | <div class="col-md-3"> | ||
<ul id="sidemenu" style="width:100%"> | <ul id="sidemenu" style="width:100%"> | ||
| − | <li><a href="#" onclick="toEvent('intro');">Introduction</a></li> | + | <li><a href="#" onclick="return toEvent('intro');">Introduction</a></li> |
| − | <li><a href="#" onclick="toEvent('pair');">Paired-difference T test</a></li> | + | <li><a href="#" onclick="return toEvent('pair');">Paired-difference T test</a></li> |
| − | <li><a href="#" onclick="toEvent('reg');">Regression & Prediction</a></li> | + | <li><a href="#" onclick="return toEvent('reg');">Regression & Prediction</a></li> |
</ul> | </ul> | ||
</div> | </div> | ||
</div> | </div> | ||
</div> <!-- /.container-fluid --> | </div> <!-- /.container-fluid --> | ||
| − | <script src="/Team:NCKU_Tainan/js/frame/T--NCKU_Tainan--jquery-1_12_0_min_js?ctype=text/javascript&action=raw"></script><script src="/Team:NCKU_Tainan/js/frame/T--NCKU_Tainan--bootstrap_min_js?ctype=text/javascript&action=raw"></script><script src="/common/MathJax-2.5-latest/MathJax.js?config=TeX-AMS-MML_HTMLorMML"></script><script src="/Team:NCKU_Tainan/js/T--NCKU_Tainan--MathjaxConfigIgem_js?ctype=text/javascript&action=raw"></script><script src="/Team:NCKU_Tainan/js/T--NCKU_Tainan--common_js?ctype=text/javascript&action=raw"></script><script>(function() { /* change icon */ var link = document.createElement('link'); link.type = 'image/x-icon'; link.rel = 'shortcut icon'; link.href = '/wiki/images/8/80/T--NCKU_Tainan--favicon.png'; document.getElementsByTagName('head')[0].appendChild(link);}());</script> | + | <script src="/Team:NCKU_Tainan/js/frame/T--NCKU_Tainan--jquery-1_12_0_min_js?ctype=text/javascript&action=raw"></script><script src="/Team:NCKU_Tainan/js/frame/T--NCKU_Tainan--bootstrap_min_js?ctype=text/javascript&action=raw"></script><script src="/common/MathJax-2.5-latest/MathJax.js?config=TeX-AMS-MML_HTMLorMML"></script><script src="/Team:NCKU_Tainan/js/T--NCKU_Tainan--MathjaxConfigIgem_js?ctype=text/javascript&action=raw"></script><script src="/Team:NCKU_Tainan/js/T--NCKU_Tainan--common_js?ctype=text/javascript&action=raw"></script><script>(function() { /* change icon */ var link = document.createElement('link'); link.type = 'image/x-icon'; link.rel = 'shortcut icon'; link.href = '/wiki/images/8/80/T--NCKU_Tainan--favicon.png'; document.getElementsByTagName('head')[0].appendChild(link);}());</script> <script src="/Team:NCKU_Tainan/js/frame/T--NCKU_Tainan--highlight_pack_js?ctype=text/javascript&action=raw"></script> |
| + | <script src="/Team:NCKU_Tainan/js/frame/T--NCKU_Tainan--highlightjs-line-numbers_js?ctype=text/javascript&action=raw"></script> | ||
| + | <script>hljs.initHighlightingOnLoad();hljs.initLineNumbersOnLoad();</script> | ||
| + | |||
| + | |||
</body></html> | </body></html> | ||
Revision as of 03:26, 11 October 2016
In medicine, the blood glucose exceeding 5mM/L implies having diabetes, and it exceeding 120mM/L implies being a severe patient. Finding the person whose glucose concentration is over 5mM/L or 120mM/L is our target. First, we prove that there has difference between 0.1mM/L and 5mM/L (120mM/L) in the paired-difference T test part. And, we use the regression and prediction intervals to distinguish exceeding 120mM/L and 5mM/L from exceeding 0.1mM/L. From the result, 5mM/L can be distinguished from 0.1mM/L after 101 minutes, and 120mM/L can be distinguished from 0.1mM/L after 88 minutes.
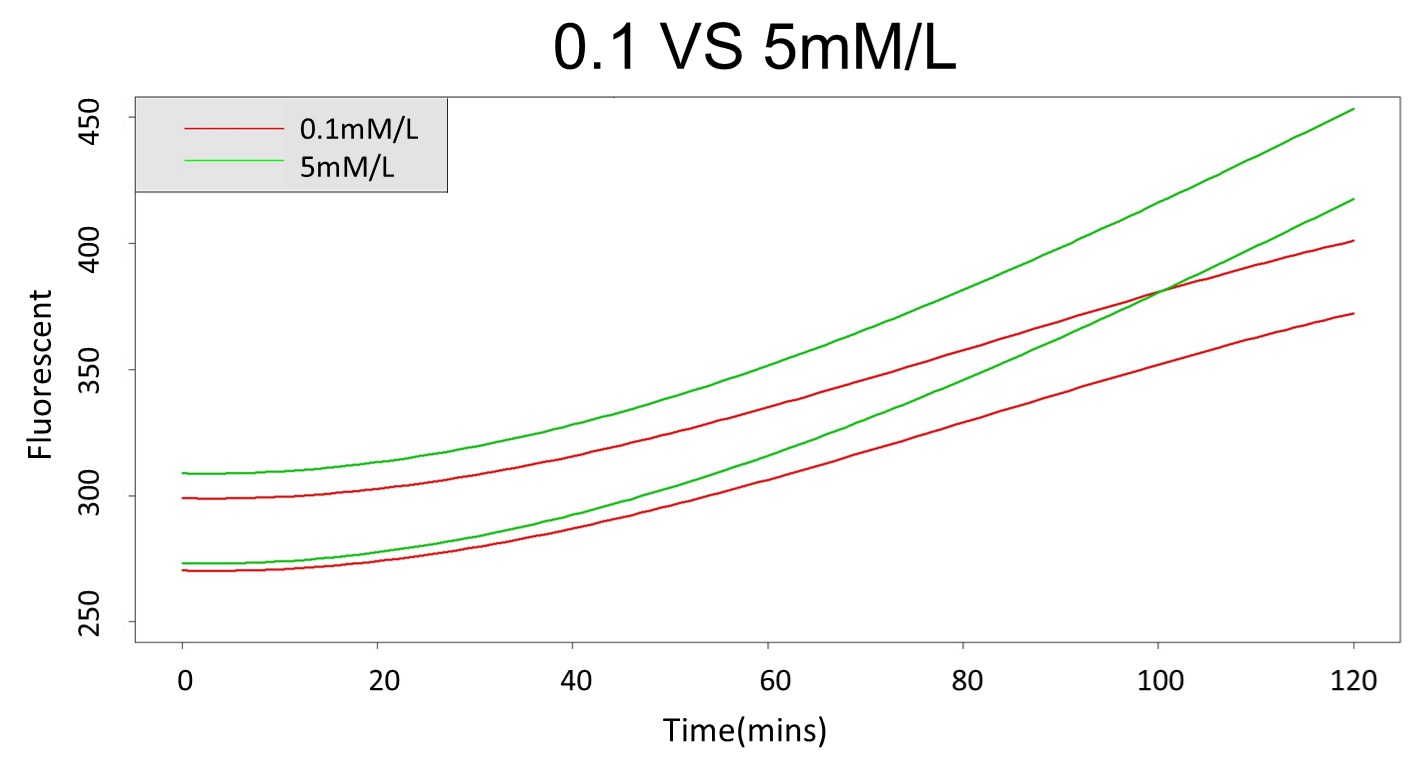
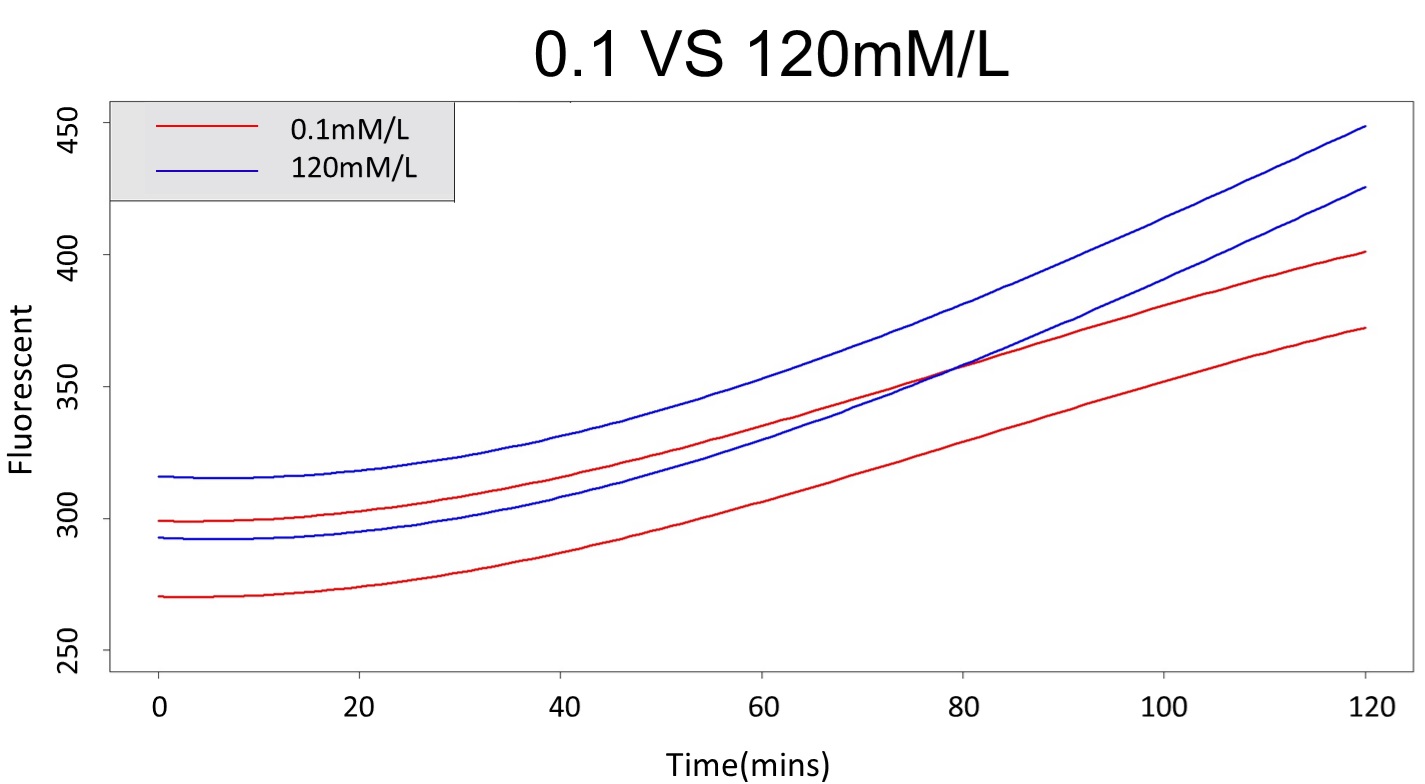
In medicine, the blood glucose exceeding 5mM/L implies having diabetes, and it exceeding 120mM/L implies being a severe patient. Hence, we use paired-difference test to analyze whether the difference of these two groups (0.1 vs 5mM/L or 0.1 vs 120mM/L) have statistical significance in this part.
Procedure
1. Guessing that there is difference over 90 minutes, we analyze the data of 0.1mM/L and 5mM/L at 90 minutes first.
(Data)
Experiment Types |
First | Second | ... | Twelfth |
|---|---|---|---|---|
| 0.1mM/L | 358 | 368 | ... | 338 |
| 5mM/L | 369 | 386 | ... | 385 |
Because the experiments of 0.1mM/L and 5mM/L have correlation and they are small sample, we choose the paired-difference test to examine whether there is difference in two groups at 90 minutes.
Analysis:
(use one-tailed test)
\(H_0:\mu_0\le0\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ H_\alpha:\mu_0\ge0\)
Because the sample is small, we choose the t distribution to test.
| d(=5mM/L-0.1mM/L) | 11 | 18 | ... | 47 |
\(n\) (Number of paired differences)=12
\(\bar{d}\) (Mean of the sample differences)= 26.16666667
\(s_d\) (Standard deviation of the sample differences) = \(\sqrt{\frac{\sum(d_i-\bar{d})^2}{n-1}}\) = 13.19664788
Test statistic t = \(\frac{\bar{d}-0}{s_d/\sqrt{n}}\) = 6.868713411 \(\gt t_{0.05,11}\) = 1.795885
P(t\(\gt\)6.868713411)= 1.995084e-05
Hence, We conclude that there is a difference between 0.1 and 5mM/L.
2. Find the minimal time at which there is statistical significance by paired-difference test.(use R program & α=0.05)
(Data)
Types Time(min) |
0.1mM/L | ... | 0.1mM/L | 5mM/L | ... | 5mM/L |
|---|---|---|---|---|---|---|
| 0 | 295 | ... | 276 | 292 | ... | 291 |
| 1 | 296 | ... | 276 | 290 | ... | 291 |
| 2 | 301 | ... | 277 | 292 | ... | 287 |
| . . . |
. . . |
... | . . . |
. . . |
... | . . . |
| 119 | 392 | ... | 372 | 420 | ... | 443 |
| 120 | 392 | ... | 374 | 427 | ... | 439 |
By using R program
\(t_{0.05,11}\) = 1.795885
statistic Time(min) |
T statistic (\(t_0\)) |
|---|---|
| 0 | 2.283227 |
| 1 | 1.992688 |
| . . . |
. . . |
| 119 | 11.908155 |
| 120 | 15.538544 |
Hence, we can find \(t_0 \gt t_{0.05,11}\) at every time.
data0.1<-read.csv("C:/Users/Rick/Desktop/NCKUactivity/iGEM/819test/0.1urine.csv",header=T)
data5<-read.csv("C:/Users/Rick/Desktop/ NCKUactivity/iGEM/819test/5urine.csv",header=T)
difference<-cbind(data5[,2]-data0.1[,2],data5[,3]-data0.1[,3],data5[,4]-data0.1[,4],data5[,5]-data0.1[,5],data5[,6]-data0.1[,6],data5[,7]-data0.1[,7],data5[,8]-data0.1[,8],data5[,9]-data0.1[,9],data5[,10]-data0.1[,10],data5[,11]-data0.1[,11],data5[,12]-data0.1[,12],data5[,13]-data0.1[,13])
dbar<-difference%*% rep(1/12,12)
var<- ((difference -rep(dbar, 12))^2%*%rep(1,12))/11
sd<-var^0.5
t<-(dbar/sd)*(12^0.5)3. Same with procedure 2, find the minimal time at which there is statistical significance by paired-difference test. (use R program, α=0.05, remove a outlier data)
By using R program
\(t_{0.05,10}\) = 1.812461
statistic Time(min) |
T statistic (\(t_0\)) |
|---|---|
| 0 | 4.720629 |
| 1 | 4.580426 |
| . . . |
. . . |
| 119 | 12.428324 |
| 120 | 14.240245 |
Hence, we can find \(t_0 \gt t_{0.05,10}\) at every time.
Conclusion:
We can say there are the difference groups (0.1 vs 5 mM/L or 0.1 vs 120mM/L) in part 1 with the data. And then, we need to find an accurate value which can distinguish between two groups.
data0.1<-read.csv("C:/Users/Rick/Desktop/ NCKUactivity/iGEM/819test/0.1urine.csv",header=T)
data120<-read.csv("C:/Users/Rick/Desktop/ NCKUactivity/iGEM/819test/120urine.csv",header=T)
difference<-cbind(data120[,2]-data0.1[,2],data120[,3]-data0.1[,3],data120[,4]-data0.1[,4],data120[,5]-data0.1[,5],data120[,6]-data0.1[,6],data120[,8]-data0.1[,8],data120[,9]-data0.1[,9],data120[,10]-data0.1[,10],data120[,11]-data0.1[,11],data120[,12]-data0.1[,12],data120[,13]-data0.1[,13])
dbar<-difference%*% rep(1/11,11)
var<- ((difference -rep(dbar, 11))^2%*%rep(1,11))/10
sd<-var^0.5
t<-(dbar/sd)*(11^0.5)Our product uses the fluorescence intensity to obtain the concentration of blood glucose. Therefore, whether we could precisely distinguish exceeding 120mM/L and 5mM/L from exceeding 0.1mM/L becomes the most important problem. We use the skill of the prediction interval in this part.
Procedure
1. Use the regression to find the model of 0.1, 5, 120mM/L, and show the prediction interval plot.
(0.1mM/L)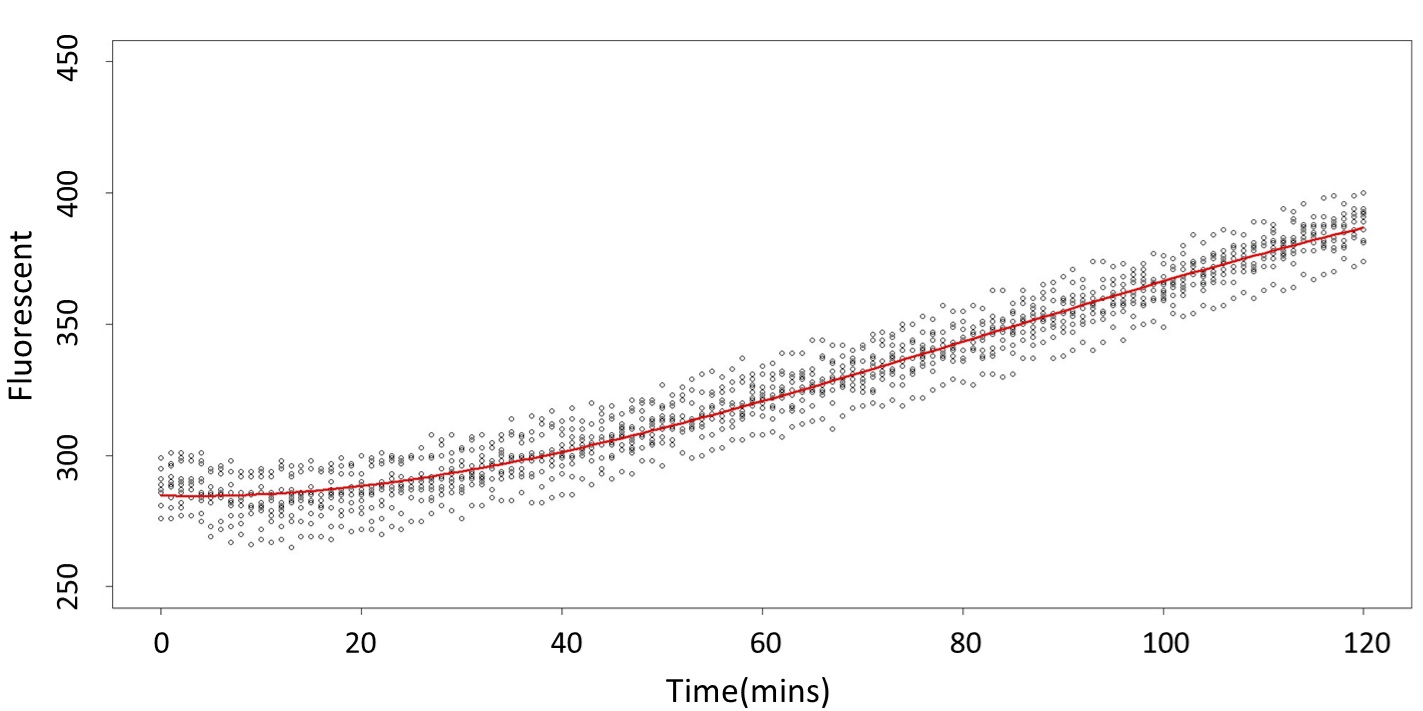
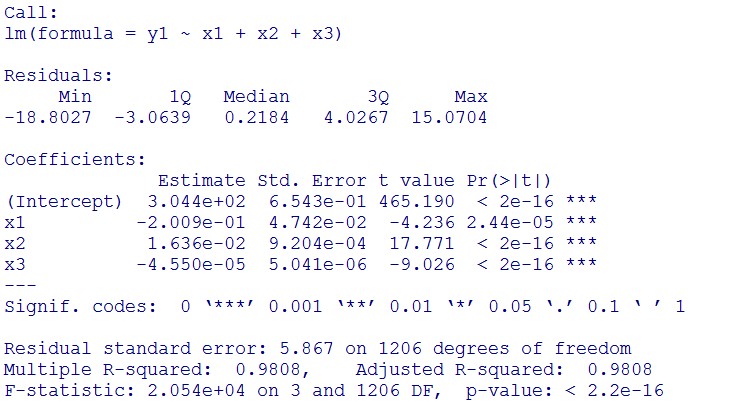
(summary)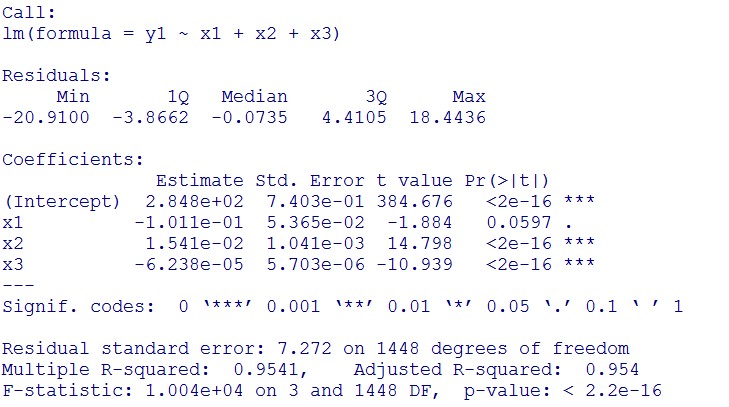
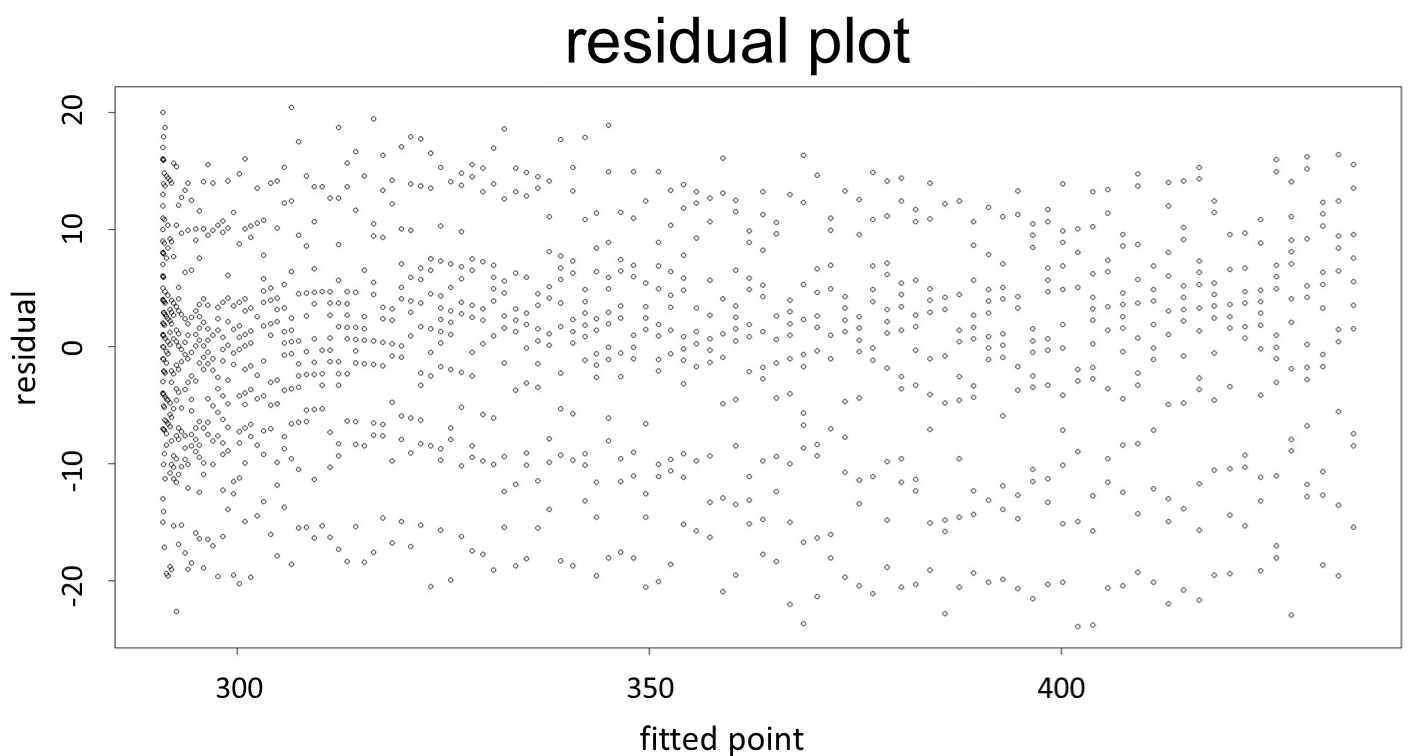
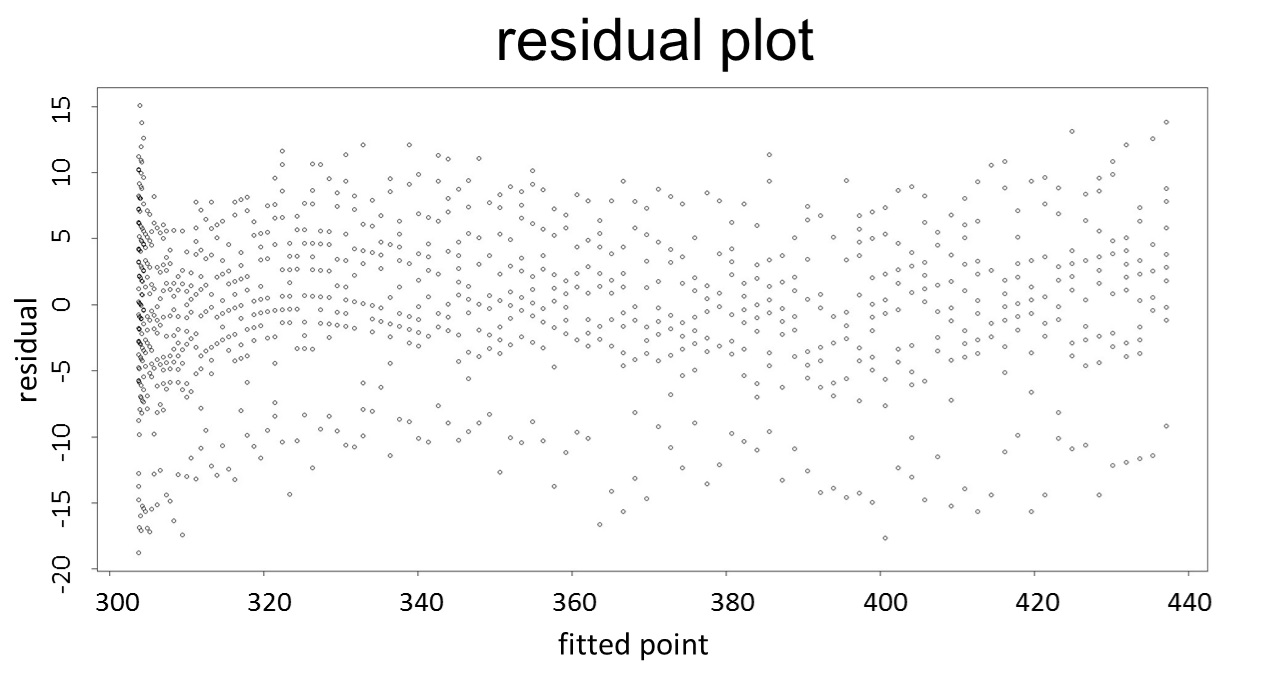
(residual plot)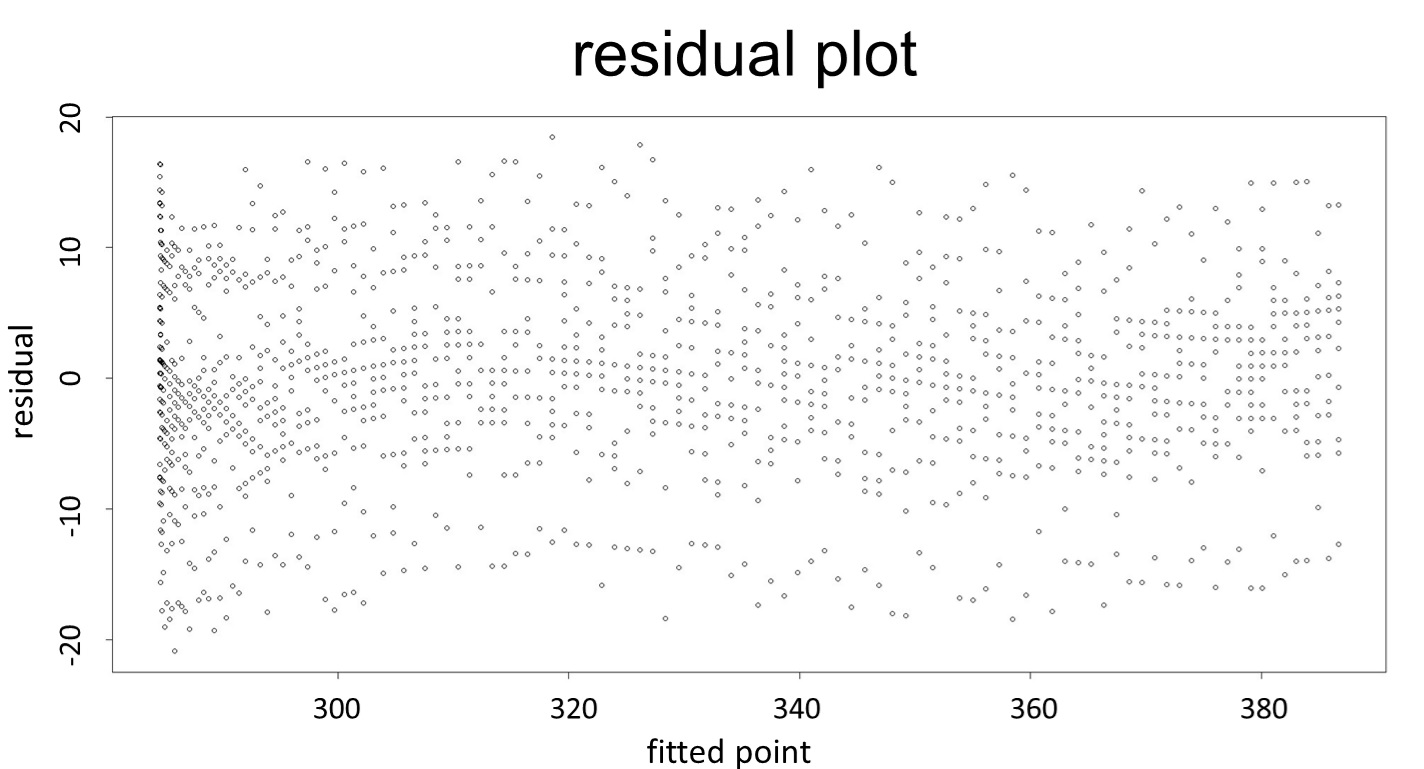
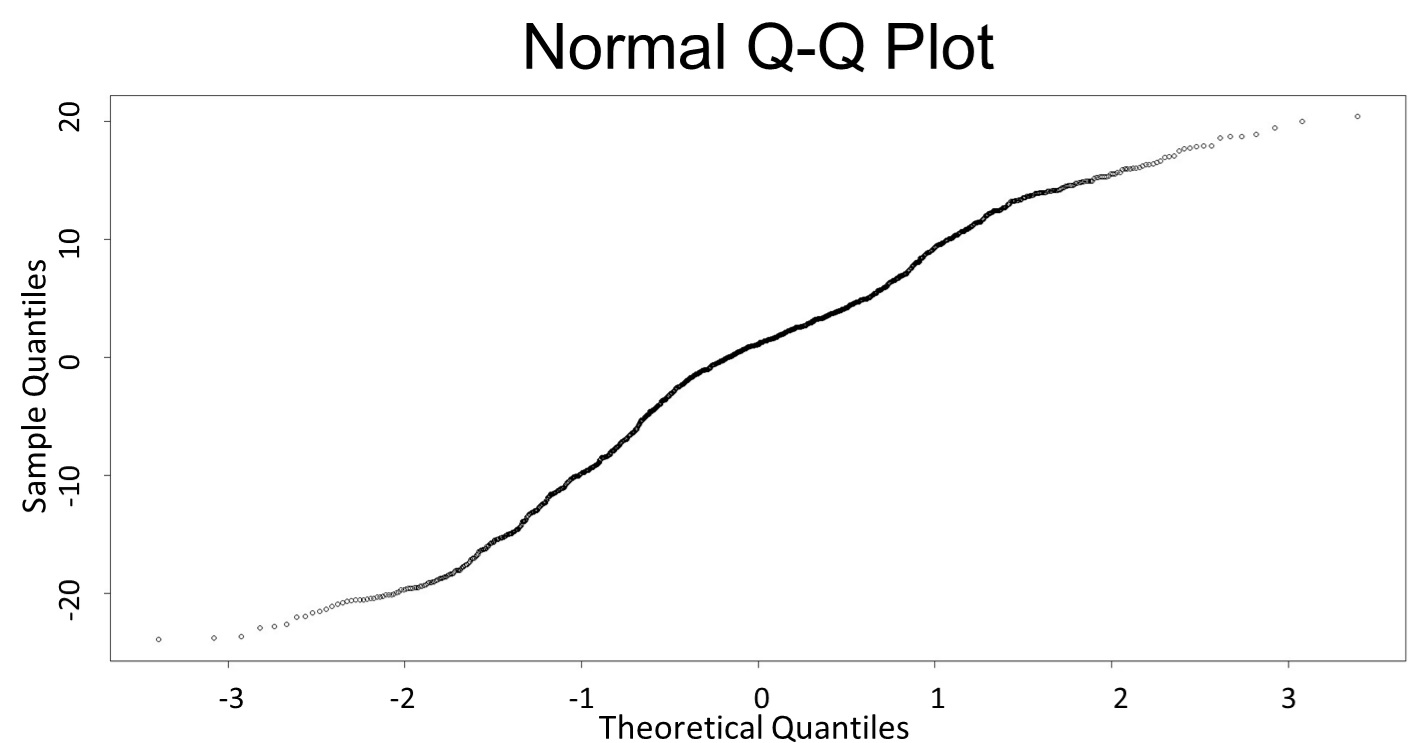
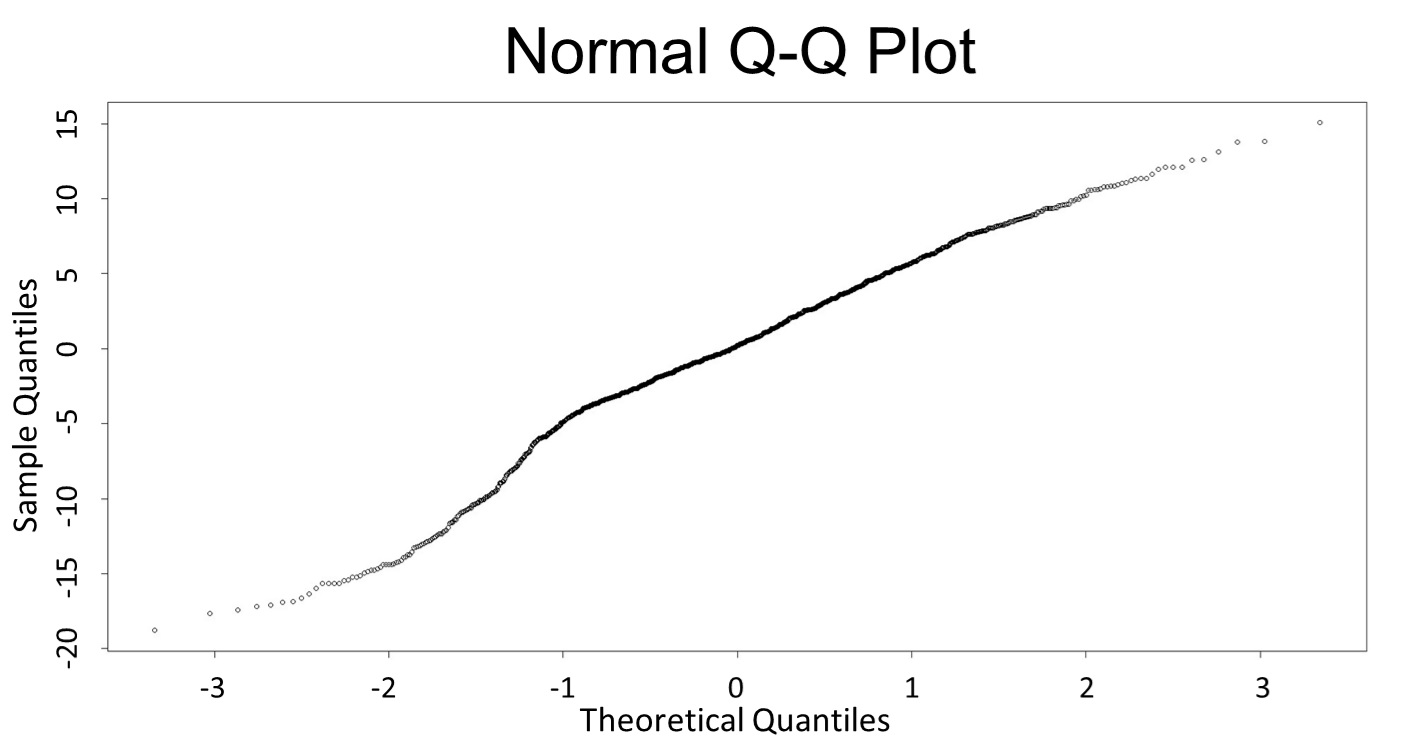
(Q-Q plot)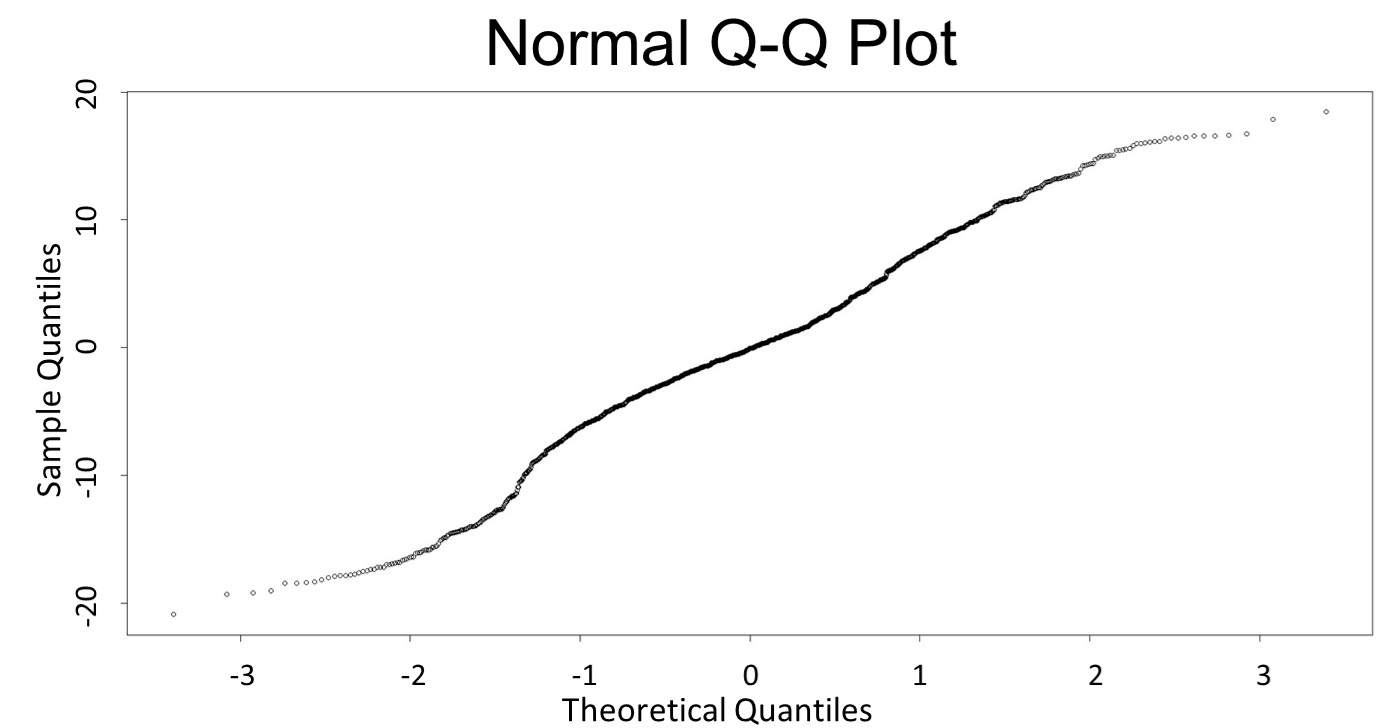
This model conforms the assumption and R-square is equal to 0.9541, so we think the cubic polynomial regression model is suitable.
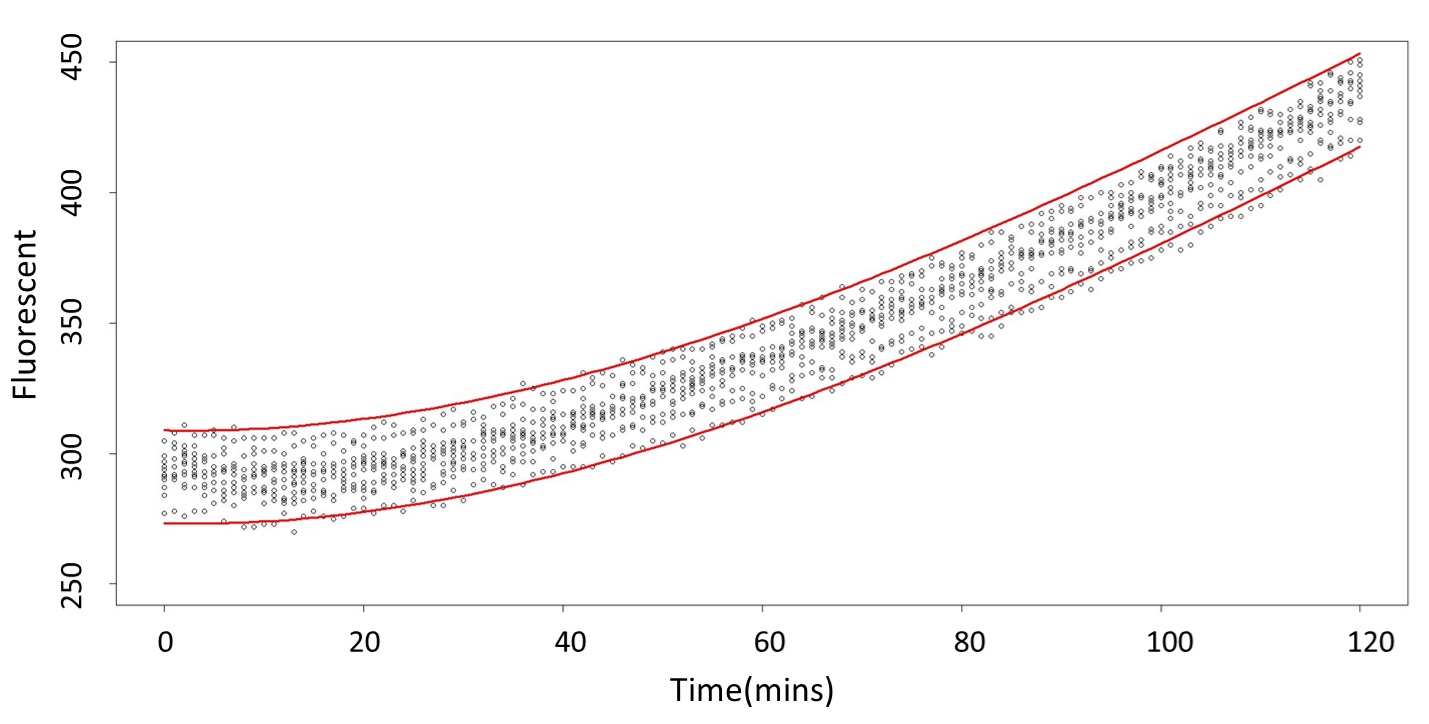
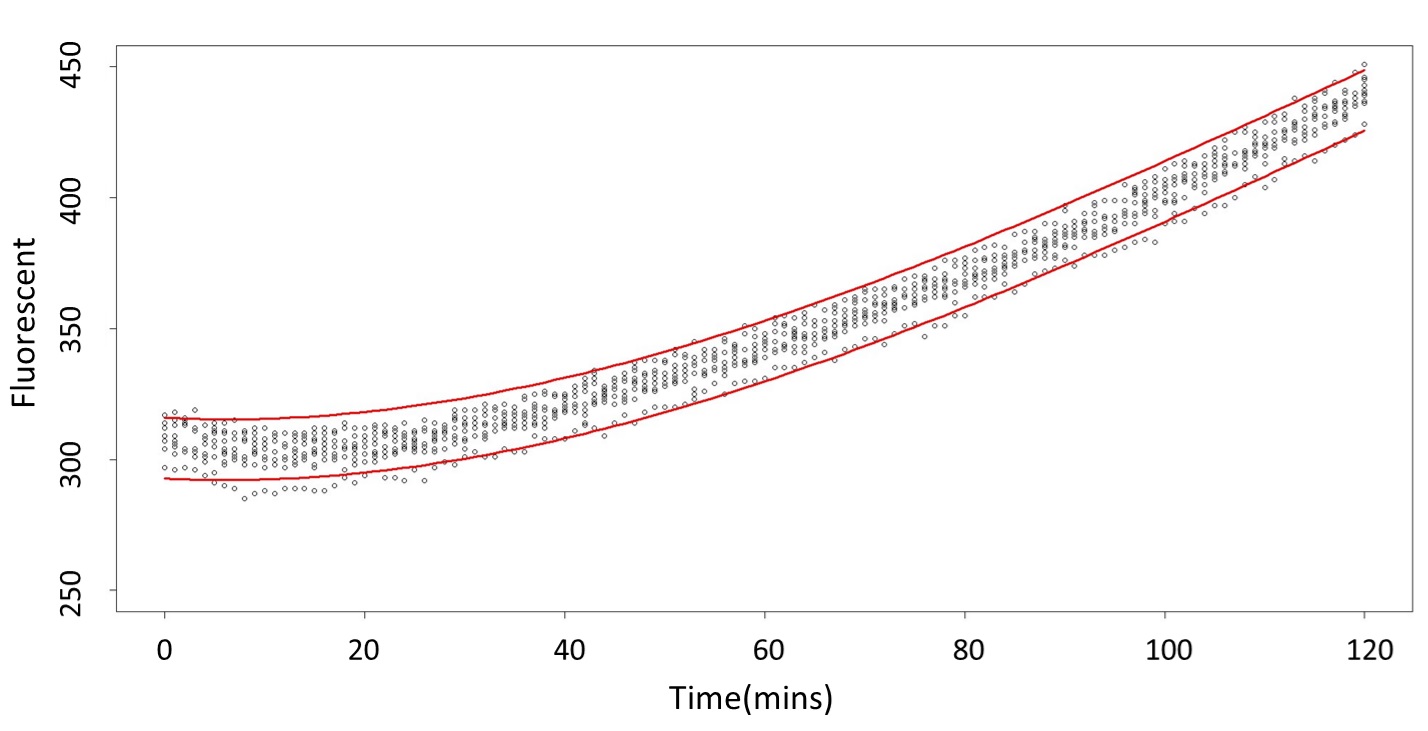
(prediction interval)
Formula: \(\bar{X}\pm t_{\frac{\alpha}{2},n-1}S\sqrt{1+\frac{1}{n}}\)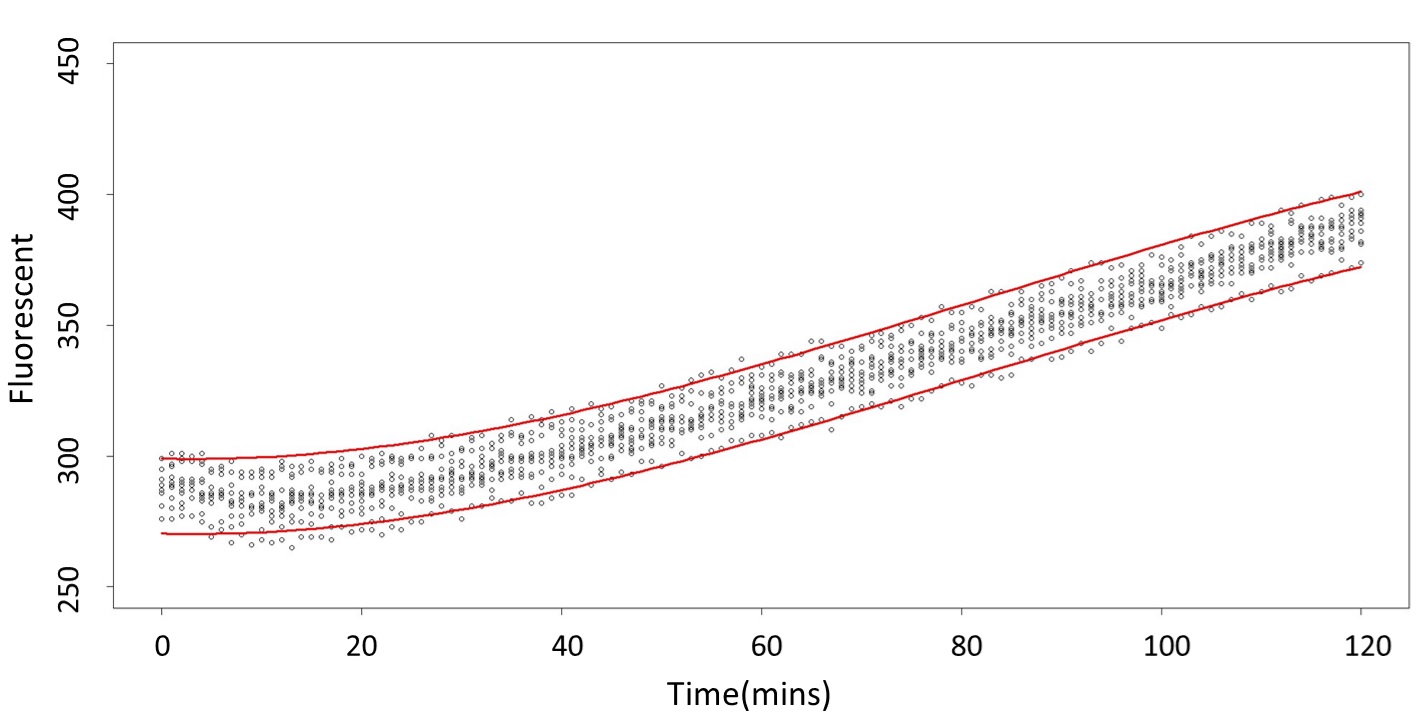
And look the following, the procedure is same in the 5mM/L and 120mM/L.
(5mM/L)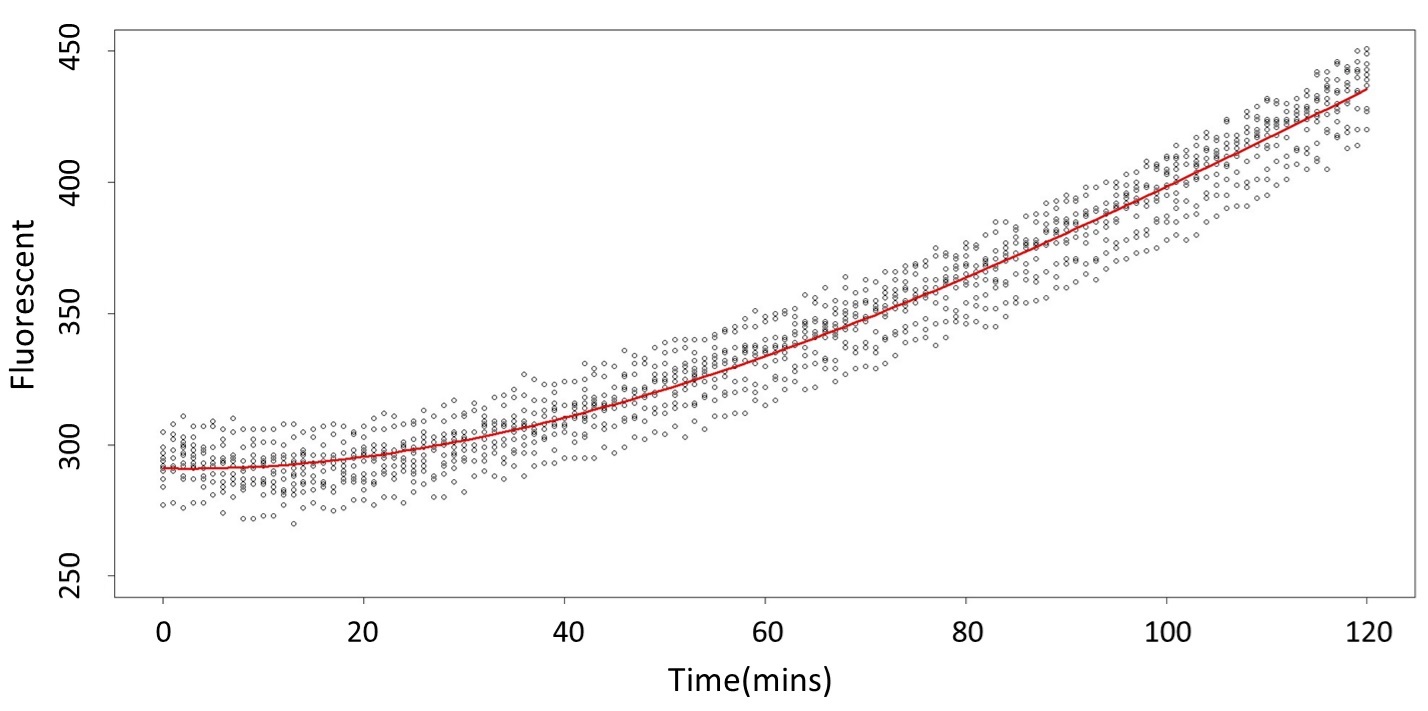

 (120mM/L)
(120mM/L)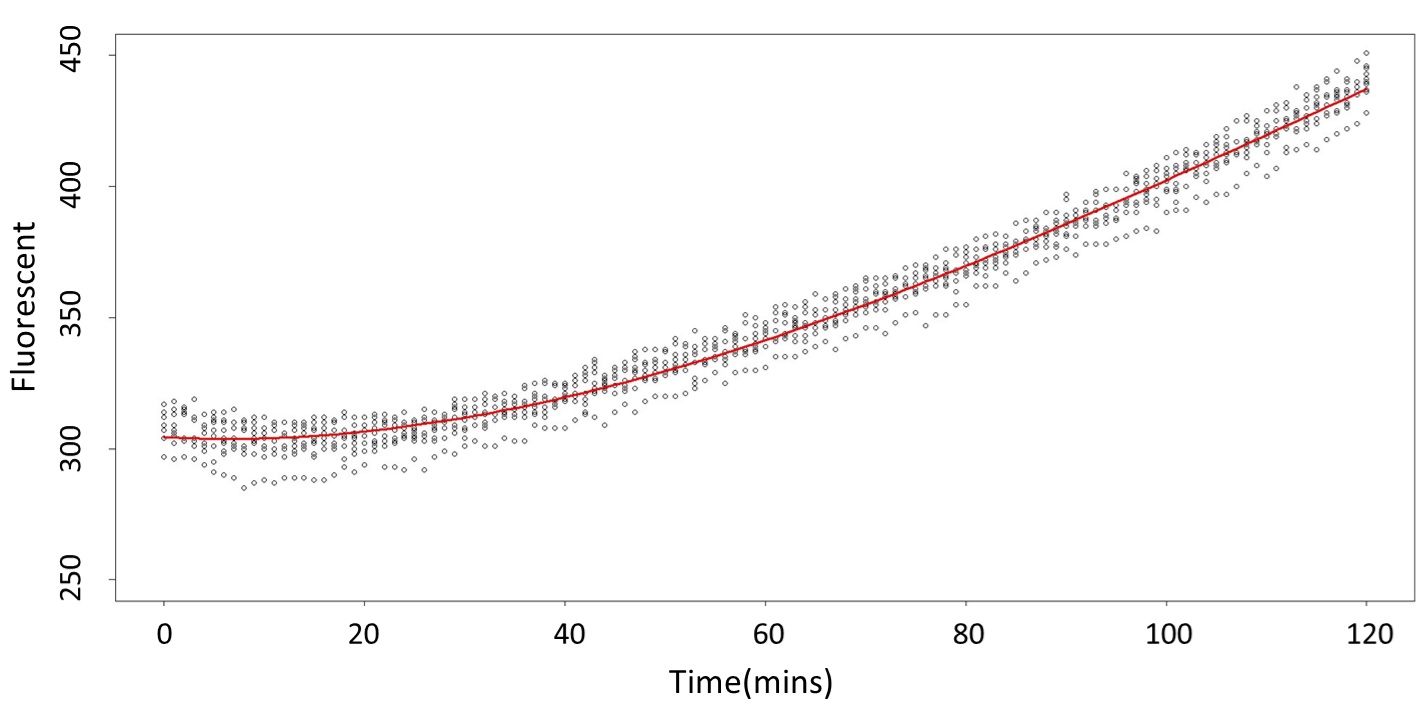
2. According to the previous part, we can say that 0.1mM/L and 5mM/L are difference group by the statistical significance. In order to precisely distinguish these two groups, choose the time at which the 5mmo/L and 0.1mmo/L prediction interval started to diverge to be the recommended prediction time.
By the above tables, we can see that 5mM/L low prediction line exceeds 0.1mM/L up prediction line when the time is more than 101 mins. Hence, it can be expected to have a higher accuracy to take the data after 101 mins.
(prediction interval of 0.1 &5 mM/L)
3. Same with procedure 2, choose the time at which the 120mmo/L and 0.1mmo/L prediction interval started to diverge to be the recommended prediction time.
By the above tables, we can find that 120mM/L low prediction line exceeds 0.1mM/L up prediction line when the time is more than 88 mins. Hence, it can be expected to have a higher accuracy to take the data in 88 mins.
(prediction interval of 0.1 &120 mM/L)
Appendix
#0.1 vs 5
#0.1 urine plot
data<-read.csv("C:/Users/Rick/Desktop/NCKUactivity/iGEM/819test/0.1urine.csv",header=T)
x1<-rep(data[,1],12)
x2<-x1^2
x3<-x1^3
y1<-c(data[,2],data[,3],data[,4],data[,5],data[,6],data[,7], data[,8],data[,9],data[,10], data[,11],data[,12],data[,13])
model<-lm(y1~x1+x2+x3)
yhat0.1<-model$fit
plot(x1,y1,ylim=c(250,450),xlab= "time(mins) ",ylab= "Fluorescent", cex.lab=1.5)
#lines(data[,1], yhat0.1[1:121],lwd=3,col=2)
n=121*12
mse<-sum((y1-yhat0.1)^2)/(n-3) # calculate MS_Res(=σ^2)
X<-cbind(1,x1,x2,x3)
se<-sqrt(mse*(1+X[1,]%*%solve(t(X)%*%X)%*%X[1,]))
up0.1<-model$coefficients[1]+x1*model$coefficients[2]+x2*model$coefficients[3]+x3*model$coefficients[4]+qt(.975,df=n-2)*se
low0.1<-model$coefficients[1]+x1*model$coefficients[2]+x2*model$coefficients[3]+x3*model$coefficients[4]+qt(.025,df=n-2)*se
lines(data[,1], up0.1[1:121], col=2,lwd=3)
lines(data[,1], low0.1[1:121],col=2,lwd=3)
#5 urine plot
data<-read.csv("C:/Users/Rick/Desktop/NCKUactivity/iGEM/819test/5urine.csv",header=T)
x1<-rep(data[,1],12)
x2<-x1^2
x3<-x1^3
y1<-c(data[,2],data[,3],data[,4],data[,5],data[,6],data[,7], data[,8],data[,9],data[,10], data[,11],data[,12],data[,13])
model<-lm(y1~x1+x2+x3)
yhat5<-model$fit
par(new=TRUE)
plot(x1,y1,ylim=c(250,450),xlab= "time(mins) ",ylab= "Fluorescent", cex.lab=1.5)
#lines(data[,1], yhat5[1:121],lwd=3,col=2)
n=121*12
mse<-sum((y1-yhat5)^2)/(n-3) # calculate MS_Res(=σ^2)
X<-cbind(1,x1,x2,x3)
se<-sqrt(mse*(1+X[1,]%*%solve(t(X)%*%X)%*%X[1,]))
up5<-model$coefficients[1]+x1*model$coefficients[2]+x2*model$coefficients[3]+x3*model$coefficients[4]+qt(.975,df=n-2)*se
low5<-model$coefficients[1]+x1*model$coefficients[2]+x2*model$coefficients[3]+x3*model$coefficients[4] +qt(.025,df=n-2)*se
lines(data[,1], up5[1:121], col=3,lwd=3)
lines(data[,1], low5[1:121], col=3,lwd=3)
title(main="0.1 vs 5mM/L",cex.main=4)
Name<-c(expression(paste("0.1mM/L")),expression(paste("5mM/L")))
legend("topleft", Name, ncol = 1, cex = 1.5, col=c("red","green"),lwd = c(2,2), bg = 'gray90')
#0.1 vs 120
#0.1 urine plot
data<-read.csv("C:/Users/Rick/Desktop/NCKUactivity/iGEM/819test/0.1urine.csv",header=T)
x1<-rep(data[,1],12)
x2<-x1^2
x3<-x1^3
y1<-c(data[,2],data[,3],data[,4],data[,5],data[,6],data[,7], data[,8],data[,9],data[,10], data[,11],data[,12],data[,13])
model<-lm(y1~x1+x2+x3)
yhat0.1<-model$fit
plot(x1,y1,ylim=c(250,450),xlab= "time(mins) ",ylab= "Fluorescent", cex.lab=1.5)
#lines(data[,1], yhat0.1[1:121],lwd=3,col=2)
n=121*12
mse<-sum((y1-yhat0.1)^2)/(n-3) # calculate MS_Res(=σ^2)
X<-cbind(1,x1,x2,x3)
se<-sqrt(mse*(1+X[1,]%*%solve(t(X)%*%X)%*%X[1,]))
up0.1<-model$coefficients[1]+x1*model$coefficients[2]+x2*model$coefficients[3]+x3*model$coefficients[4]+qt(.975,df=n-2)*se
low0.1<-model$coefficients[1]+x1*model$coefficients[2]+x2*model$coefficients[3]+x3*model$coefficiens[4]+qt(.025,df=n-2)*se
lines(data[,1], up0.1[1:121], col=2,lwd=3)
lines(data[,1], low0.1[1:121],col=2,lwd=3)
#120 urine plot
data<-read.csv("C:/Users/Rick/Desktop/NCKUactivity/iGEM/819test/120urine.csv",header=T)
x1<-rep(data[,1],10)
x2<-x1^2
x3<-x1^3
y1<-c(data[,2],data[,3],data[,4],data[,5],data[,6],data[,9],data[,10],data[,11],data[,12],data[,13])
model<-lm(y1~x1+x2+x3)
yhat120<-model$fit
par(new=TRUE)
plot(x1,y1,ylim=c(250,450),xlab= "time(mins) ",ylab= "Fluorescent", cex.lab=1.5)
#lines(data[,1], yhat120[1:121],lwd=3,col=2)
n=121*10
mse<-sum((y1-yhat120)^2)/(n-3) # calculate MS_Res(=σ^2)
X<-cbind(1,x1,x2,x3)
se<-sqrt(mse*(1+X[1,]%*%solve(t(X)%*%X)%*%X[1,]))
up120<-model$coefficients[1]+x1*model$coefficients[2]+x2*model$coefficients[3]+x3*model$coefficients[4]+qt(.975,df=n-2)*se
low120<-model$coefficients[1]+x1*model$coefficients[2]+x2*model$coefficients[3]+x3*model$coefficients[4]+qt(.025,df=n-2)*se
lines(data[,1], up120[1:121], col=4,lwd=3)
lines(data[,1], low120[1:121], col=4,lwd=3)
title(main="0.1 vs 120mM/L",cex.main=4)
Name<-c(expression(paste("0.1mM/L")),expression(paste("120mM/L")))
legend("topleft", Name, ncol = 1, cex = 1.5, col=c("red","green"),lwd = c(2,2), bg = 'gray90')
