U.coli uses promoter Pl, which can be inhibited by CRP and indirectly induced by glucose, to produce fluorescent protein. Because the process that glucose induces the promoter is not a direct process, there are a lot of compound involve in it and form a network.
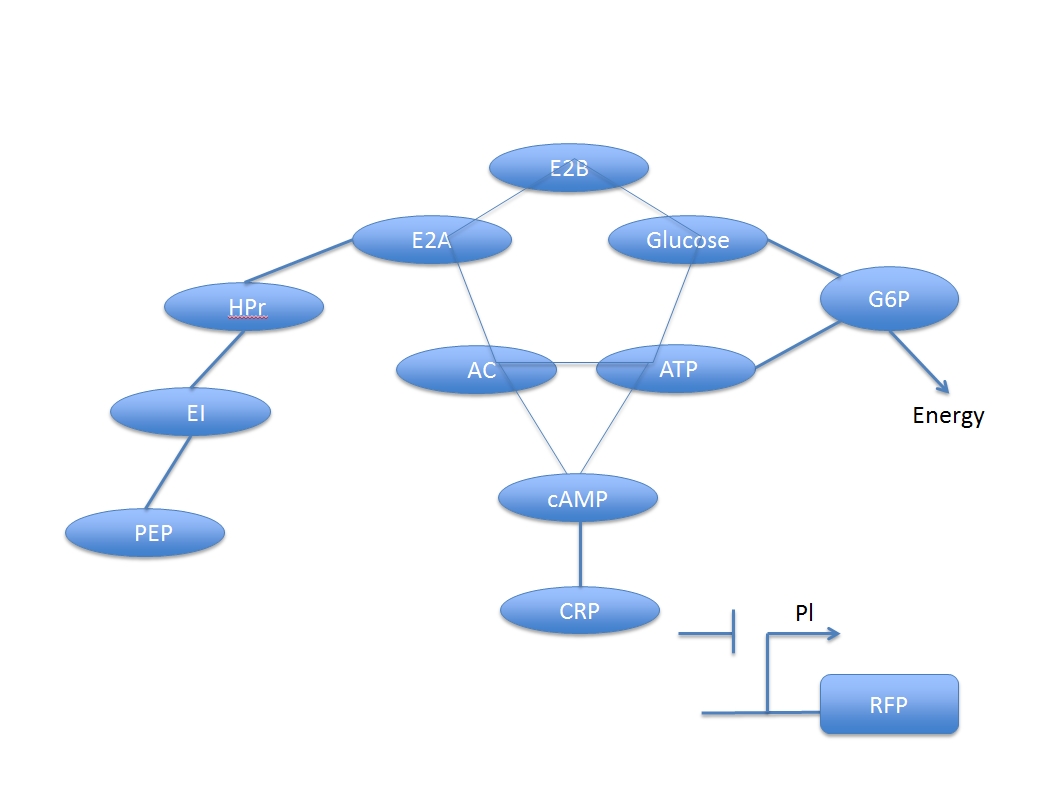
This network is composed of two main systems: glucose digest system and CRP activation system, which are competitive to each other.
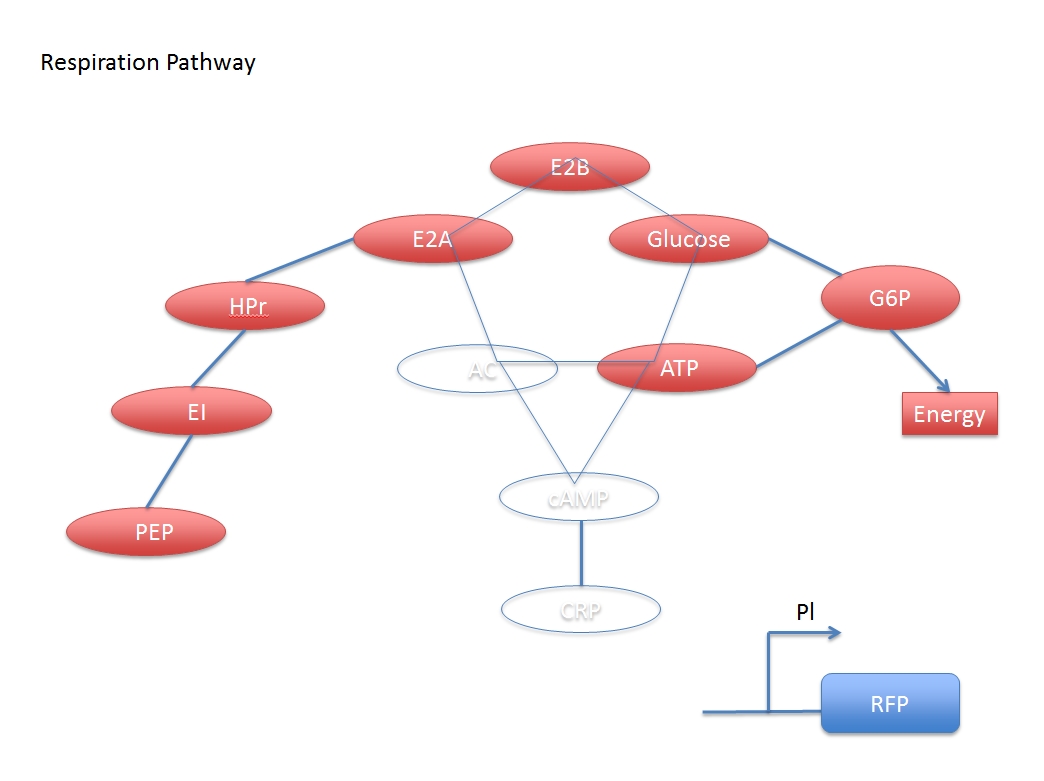
When glucose is added, some related compound will decrease during the reaction chain, and finally the concentration of activated CRP will also decrease, which means the CRP inhibited promoter Pl can express more following gene with the addition of glucose.
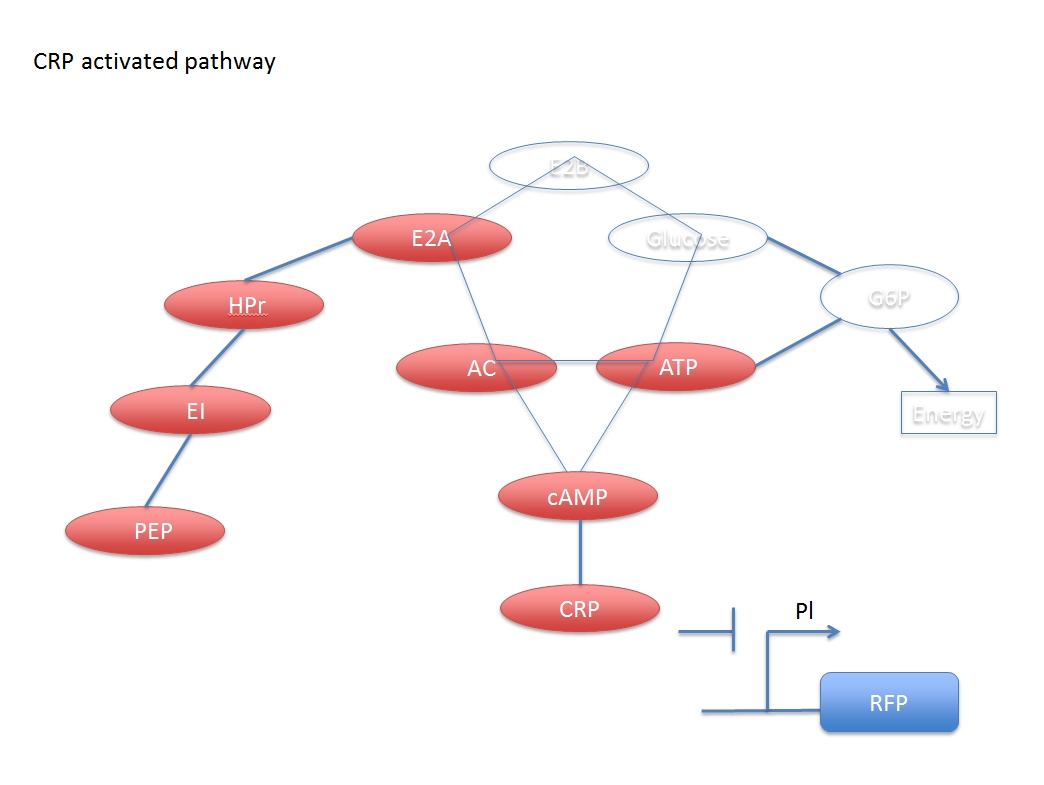
Obviously, the concentration of adding glucose and the activated CRP have negative correlation. But if we want to assay the concentration of inputted glucose numerically, we have to derive a formula base on these chemical pathways.
According to reference (1) we can list the following reaction to simply represent the reaction chain involve in the whole process.
\((PEP-Pi)+E1\leftrightarrow PEP+(E1-Pi)\)
\((E_1-Pi)+HPr\leftrightarrow E_1+(HPr-Pi)\)
\((HPr-Pi)+E2A\leftrightarrow (E2A-Pi)+HPr\)
when glucose participate:
\((E2A-Pi)+E2B\leftrightarrow E2A+(E2B-Pi)\) \(---(A)\)
\((E2B-Pi)+Glucose\overset{E2C}{\rightarrow} E2B+G6P\) \(---(B)\)
\(G6P\underset{Respiration}{\rightarrow}Energy\) \(---(C)\)
when glucose absence:
\((E2A-Pi)+AC\leftrightarrow E2A+(AC-Pi)\) \(---(D)\)
\(ATP\overset{(AC-Pi)}{\rightarrow} cAMP\) \(---(E)\)
\(cAMP+CRPx\leftrightarrow CRP\) \(---(F)\)
\(CRP+Pl\leftrightarrow Plx\) \(---(G)\)
\(Pl+polymerase+\{nucleotides\}\rightarrow Pl+polymerase+mRNA\) \(---(H)\)
Before we get everything started, we first make an assumption so that we can simplify this dynamics considerably.
Assumption 1:
The variation of \(\frac{\Delta[E2A]}{[E2A]}\) is quite small, so we ignore the influence of E2A production reaction chain.
The following derivation can only be valid if the assumption above is reasonable.
Note: k represent reaction rate constant, K represent reaction equilibrium constant.
Because reaction E,F,G and B,C involve enzyme reaction, which means the steady state will be reached in a very short time (~seconds), we will deal with them first at Part I to Part III.
If we only see reaction (F) to (H), it can be seen as a modified form of induced system whereas CRP is an inhibitor activated by cAMP.
\(\frac{d[mRNA]}{dt}=k_H[Pl][Poly]\prod \{nucleotides\}\)
\(\frac{d[Pl]}{dt}=-k_G[CRP][Pl]+k_{-G}[Plx]\)
if Pl reach its steady state in a very short time, compared to the change of [CRP], that
\(\frac{d[Pl]}{dt}=0\)
then,
\([Pl]=\frac{k_{-G}}{k_G[CRP]+k_{-G}}[Pl_{total}]=\frac{1}{1+K_G[CPR]}[Pl_{total}]\)
where \(K_G=k_G/k_{-G}\), \([Pl_{total}]=[Pl]+[Plx]\)
Then the transcription rate will become
\(\frac{d[mRNA]}{dt}=k_H[Pl][Poly]\prod \{nucleotides\}=\frac{k_H[Poly]\prod\{nucleotides\}}{1+K_G[CRP]}[Pl_{total}]\)
Because nucleotides in biology system is large enough, we can treat it as a constant during the reaction.
Set \(V_s=k_H[Pl][Ploy]\prod\{nucleotides\}[Pl_{total}]\), then
\(\frac{d[mRNA]}{dt}=\frac{V_s}{1+K_G[CRP]}\)
Then we turn to the dynamics of [CRP]
From reaction (F)
\(\frac{d[CRP]}{dt}=k_F[cAMP][CRPx]-k_{-F}[CRP]\)
When [CRP] reach its steady state,
\([CRP]=\frac{[CRP_{total}][cAMP]}{K_F+[cAMP]}\)
so the transcription rate become
\(\begin{split} \frac{d[mRNA]}{dt}&=\frac{V_s}{1+K_G[CRP]}\\&=\frac{V_s(K_F+[cAMP])}{(K_F+[cAMP])+K_G[CRP_{total}][cAMP]} \\ &=\frac{K_F\frac{1}{[cAMP]}+1}{\frac{K_F}{V_S}\frac{1}{[cAMP]}+\frac{K_G[CRP_{total}]}{V_S}}\end{split} \)
We can see that the transcription rate of genes is a function of [cAMP]
cAMP actually participate many biological system not listed here. But briefly, we can assume that it is a first order reaction,
\(\frac{d[cAMP]}{dt}|_{consume}=-d_{cAMP}[cAMP]\)
according to reaction (E) and (F),
\(\frac{d[cAMP]}{dt}=k_E\frac{AC'_{total}[ATP]}{[ATP]+K_E}-d[cAMP]-\frac{d[CRP]}{dt}\)
Because in part I, [CRP] in steady state require the concentration of cAMP, which means the whole process will be very complicated if [cAMP] will keep changing with [CRP], so an assumption is needed to make the calculation simpler.
Assumption 2:
The reaction of [CRP] contribute very small to [cAMP], that is,
\(k_E\frac{[AC'_{total}][ATP]}{[ATP]+K_E}-d[cAMP]-\frac{d[CRP]}{dt}\approx k_E\frac{[AC'_{total}][ATP]}{[ATP]+K_E}-d[cAMP]\)
Under the assumption, the equilibrium of [cAMP] will be very easy to get,
\(\frac{d[cAMP]}{dt}=k_E\frac{[AC'_{total}][ATP]}{[ATP]+K_E}-d[cAMP]\)
so,
\([cAMP]=\frac{k_E}{d}\frac{[ATP]}{[ATP]+K_E]}[AC'_{total}]\)
The Glucose transmission and digestion are described in reference [1],
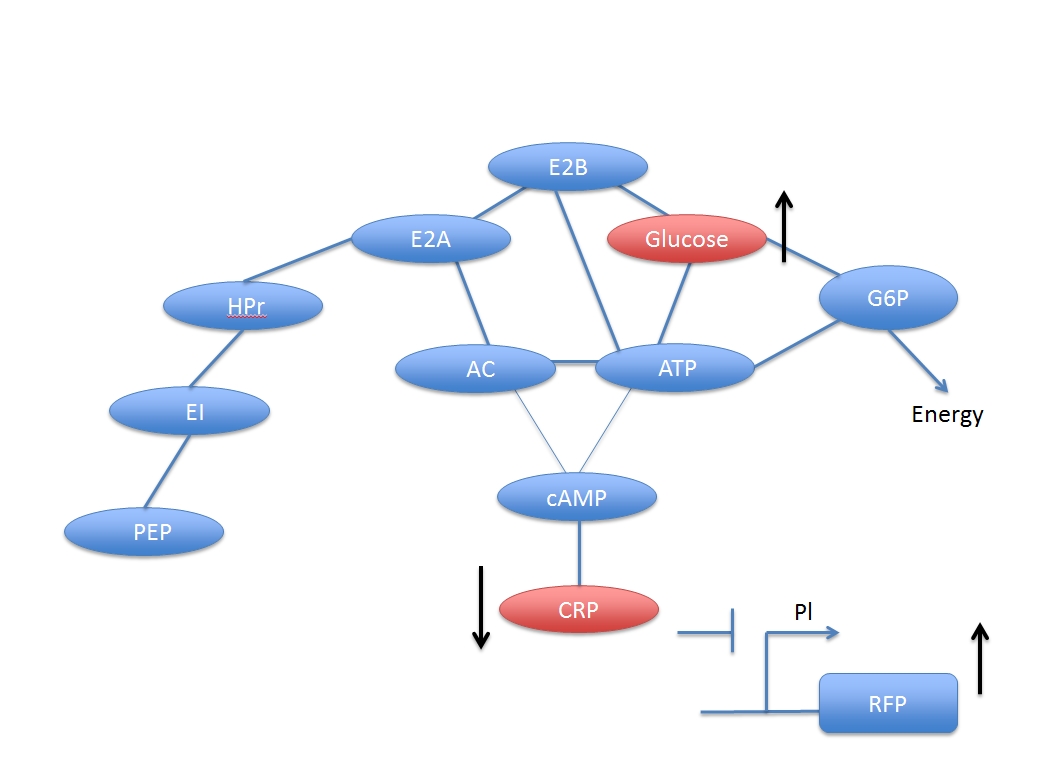
If we write reaction (B) in a more detail way,
\(E2B'+Glucose+E2C\leftrightarrow complex+Glucose\overset{k_{cat}}{\rightarrow}E2B+E2C+G6P\)
then
\(\frac{d[complex]}{dt}=k_B[E2B'][Glucose][E2C]-(k_{-B}+k_{cat}[complex][Glucose])\)
When [complex] reach its steady state so that
\(\frac{d[complex]}{dt}=0\)
then
\([complex]=\frac{k_B[E2B'][E2C]}{(k_{-B}+k_{cat})}\)
here we introduce an assumption
Assumption 3:
[complex] is very dilute so that [Glucose] will keep its concentration during the reaction chain.
We combine this result and calculate reaction (A) and get
\(\frac{d[E2B']}{dt}=-k_B[E2B'][Glucose][E2C]+k_{-B}[complex][Glucose]+k_A[E2A'][E2B]-k_A[E2A][E2B'c]\)
When E2B’ reach its steady state so that
\(\frac{d[E2B']}{dt}\)=0
then
\([E2B']=\frac{k_{-B}[complex][Glucose]+k_A[E2A'][E2B]}{k_B[E2C][Glucose]+k_{-A}[E2A]}\)
\([E2B]=\frac{k_{-B}[complex][Glucose]+k_A[E2A'][E2B_{total}]}{k_B[E2C][Glucose]+k_{-A}[E2A]}-\frac{k_A[E2A'][E2B']}{k_B[E2C][Glucose]+k_{-A}[E2A]}\)
\([E2B']=\frac{k_{-B}[complex][Glucose]+k_A[E2A'][E2B_{total}]}{k_B[E2C][Glucose]+(k_{-A}[E2A_{total}]+(k_A-k_{-A})[E2A'])}\)
Assumption 4:
Because [E2A] and [E2A’] are regulated by a lot of chemical compound, which makes [E2A’] and [E2A] not change considerably after a few amount of Glucose is added into the system.
At reaction (A) and (D), reaction don’t involve enzyme reaction, so we will calculate in Part IV and treat it as a most time-consuming reaction in the whole process.
Here, our target is to find our [AC’] when it reaches steady state.From (A) and (D). Obviously, it is a competitive reaction.
We here have two equilibrium constants
\(K_A=\frac{[E2A][E2B']}{[E2A'][E2B]}\)
\(K_B=\frac{[E2A][AC']}{[E2A'][AC]}\)
so
\(\frac{K_A}{K_B}=\frac{[E2B'][AC]}{[E2B][AC']}=\frac{[E2B']([AC_{total}]-[AC'])}{([E2B_{total}])[AC']}\)
Reassemble and get
\([AC']=\frac{K_B[B2B'][AC_{total}]}{K_A([E2B_{total}]-[E2B'])+K_B[E2B']}=\frac{K_B[AC_{total}]}{K_A[E2B_{total}]/[E2B']+(K_B-K_A)}\)
Here we have calculated the concentration of [AC’], [E2B’] and [cAMP] in Part II ~ Part VI, and we also derive a formula that can express the transcription rate of the genes following to the promoter Pl in Part I.
First, we substitute [E2B’] into [AC’] and get
\( [AC'] = \frac{K_B[AC_{total}]}{K_A[E2B_{total}]/[E2B']+(K_B-K_A)}=\frac{a[Glucose]+b}{[Glucose]+c} \)
where
\(a=\frac{K_B[AC_{total}]k_{-B}[complex]}{K_A[E2B_{total}]+(K_B-K_A)k_{-B}[complex]}\)
\(b=\frac{K_B[AC_{total}]k_A[E2A'][E2B_{total}]}{K_A[E2B_{total}]k_B[E2C]+(K_B-K_A)k_{-B}[complex]}\)
\(c=\frac{K_A[E2B_{total}](k_{-A}[E2A_{total}+(k_A-k_{-A})[E2A']])+(K_B-K_A)k_A[E2A'][E2B_{total}]}{K_A[E2B_{total}]k_B[E2C]+(K_B-K_A)k_{-B}[complex]}\)
Then put this into [cAMP]
\([cAMP]=\frac{k_E}{d}\frac{[ATP]}{[ATP]+K_E}\times \frac{a[Glucose]+b}{[Glucose]+c}=\frac{a'[Glucose]+b}{[Glucose]+c}\)
\(a'=\frac{k_E}{d}\frac{[ATP]}{[ATP]+K_E}\times \frac{K_B[AC_{total}]k_{-B}[complex]}{K_A[E2B_{total}]k_B[E2C]+(K_B-K_A)k_{-B}[complex]}\)
then, we can substitute [cAMP] into the formula of transcription
\(\begin{split}\frac{dY}{dt}&=\frac{K_F\frac{1}{[cAMP]}+1}{\frac{K_F}{V_S}\frac{1}{[cAMP]}+\frac{K_G[CRP_{total}]}{V_S}}\\&=\frac{K_F([Glucose]+c)+(a'[Glucose]+b)}{\frac{K_F}{V_S}([Glucose]+c)+\frac{K_G[CRP_{total}]}{V_S}(a'[Glucose]+b)}\\&=\frac{(K_F+a')[Glucose]+(b+K_Fc)}{(\frac{K_G[CRP_{total}]}{V_S}+\frac{K_F}{V_S})[Glucose]+(\frac{K_F}{V_S}c+\frac{K_G[CRP_{total}]}{V_S}b)}\\&=\frac{c1[Glucose]+c2}{[Glucose]+c3}\end{split}\)
where
\(c1=(K_F+a')/(\frac{K_G[CRP_{total}]}{V_S}+\frac{K_F}{V_S})\)
\(c2=(b+K_Fc)/(\frac{K_G[CRP_{total}]}{V_S}+\frac{K_F}{V_S})\)
\(c3=(\frac{K_F}{V_S}c+\frac{K_G[CRP_{total}]}{V_S}b)/(\frac{K_G[CRP_{total}]}{V_S}+\frac{K_F}{V_S})\)
For the correction of cooperativity, we add a Hill parameters, n, on the equation, so that the final formula will become
\(\frac{d[Gene]}{dt}=\frac{c1\times [Glucose]^n+c2}{[Glucose]^n}+c3\)
After a derivation of transcription rate in single cell, we now have to exam if the function can correctly match the experimental data well.
For the fitting data, we differentiate the fluorescence value obtained from photometer, take the differential to get the production rate and fetch out the value when system reach its equilibrium state, fitting the equilibrium production rate with Glucose concentration concentration that lower than 60 mg/μL and get
\(\frac{dY}{dt}=\frac{17.05\times [Glucose]^{1.18}+16.07}{[Glucose]^{1.18}+4.04}\)

The result shows that the fitting curve can fit the data well.
In our case, we want to use the formula to calculate the glucose concentration using the given fluorescence value. It is obvious that if the detected glucose concentration is lower than 30 mg/μL, U.coli can predict the glucose concentration with relatively high robustness. But if the inputted glucose concentration is higher than 30 mg/μL, it is hard to exam the glucose concentration numerically
[1] Glucose Transport in Escherichia coli Mutant Strains with Defects in Sugar Transport Systems, Journal of Bacteriology, Sonja Steinsiek and Katja Bettenbrock
[2] Glucose uptake regulation in E. coli by the small RNA SgrS: comparative analysis of E. coli K-12 (JM109 and MG1655) and E. coli B (BL21), Microbial Cell Factories,Alejandro Negrete, Weng-Ian Ng, Joseph Shiloach

