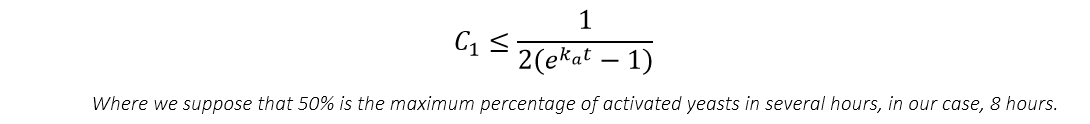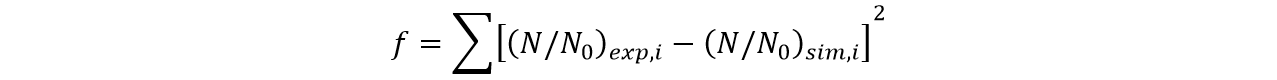Team:SJTU-BioX-Shanghai/Yeast activation

• home
• Project
  • Description
  • Motivation
  • Design as a whole
  • Yeast glucose sensor
  • Yeast epinephrine sensor
  • Yeast biosensor as freeze-dried powders
  • Vision for the future
  • Protocols
  • Notebook
  • Results
  • Proof
• Safety
• Parts
  • Team Parts
  • Composite Parts
• Model
  • Yeast activation
  • Yeast luminescence process
  • Combination and use
• Human Practice
  • Introduction
  • Bioethics
  • Hospital Experiencing
  • Marketing
  • Medical Service
  • Outreach
  • Integrated Practices
• Achievement
  • Achievement
  • Human Practice:Gold and Silver
• Team
  • Team
  • Collaborations
  • Attributions

Yeast activation

Description

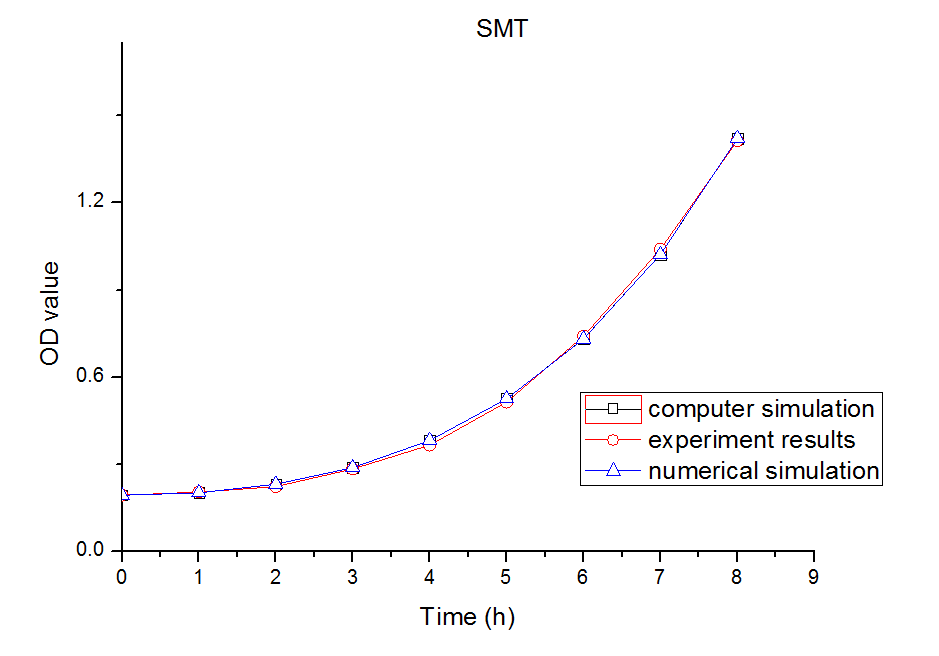
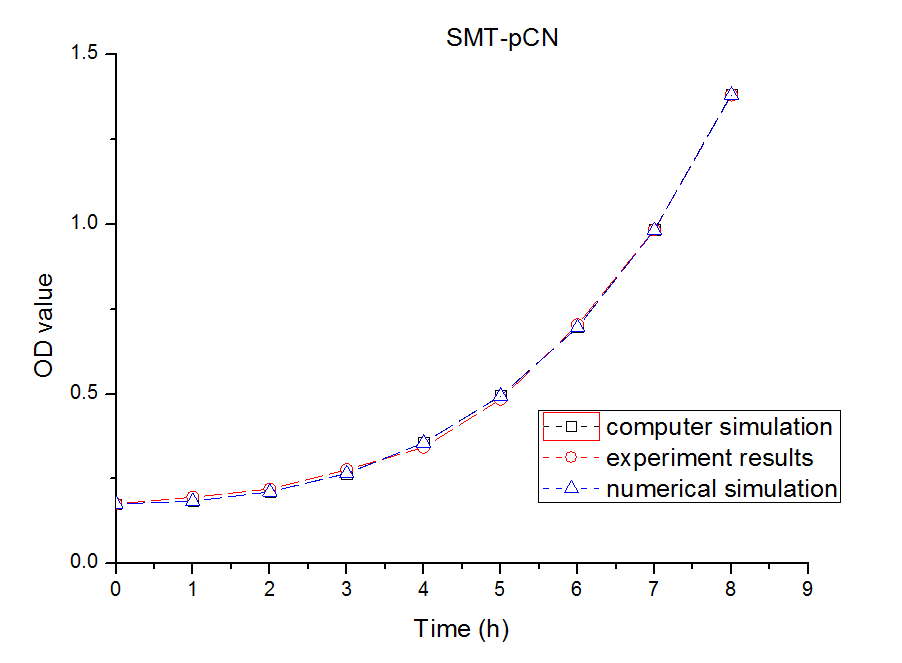
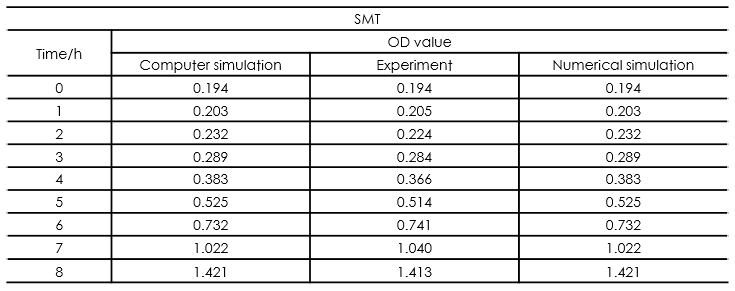
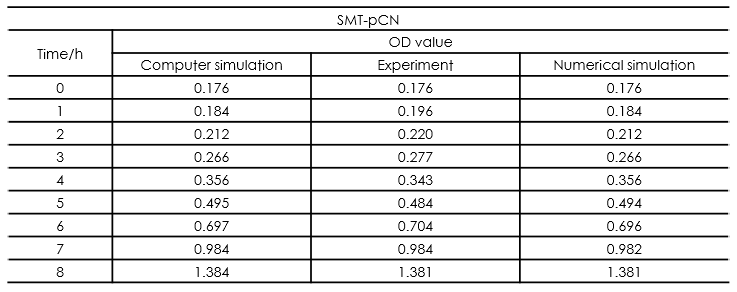
In this part, we established a model for the activation process of dry yeasts by simulating the total number of cells corresponding to time. Since the time period we consider is long enough for activated yeast to proliferate, the proliferation process is considered in this model. After the parameters in the model were adjusted, we found that our simulation results fits experiment results well.

Basic assumption

1. all yeasts are inactivated at first.
2. only activated yeasts can proliferate.
3. yeasts’activation process is so slow that not much yeasts are activated even after hours.
4. some yeast are dead initially.

Formula and derivation

The activation process of the cells corresponding to time

We assume the activation process of yeasts is as follows:

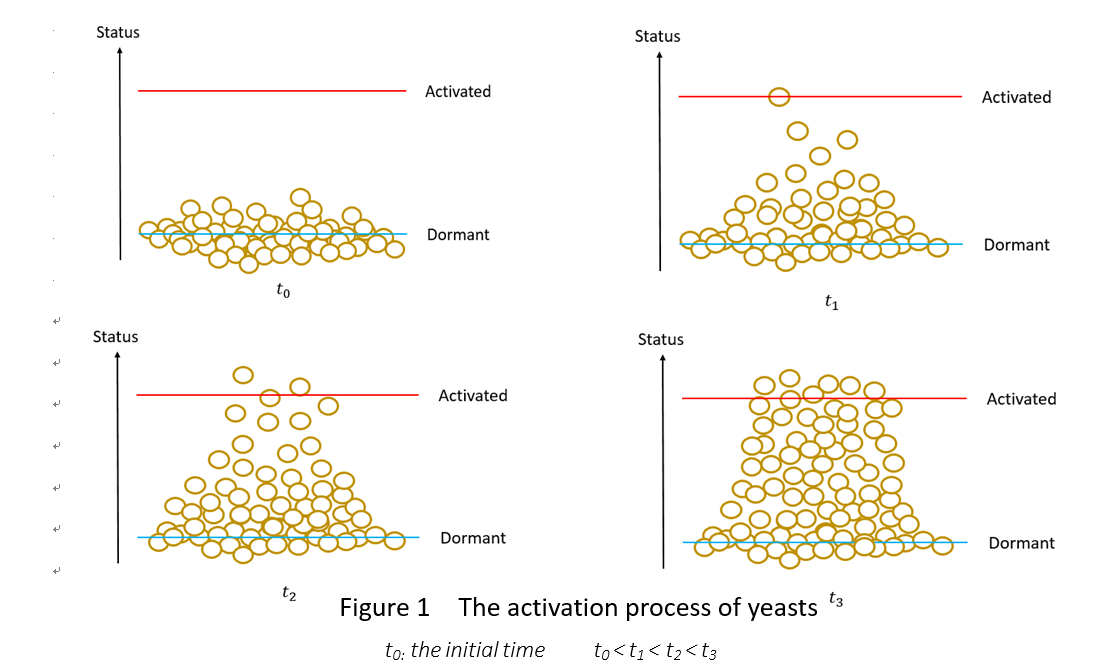
In the beginning, all the cells are in the status of dormant. To t₁, a few have been activated and most cells are around the status of dormant. To t₂, some cells have been activated and the number of the cells around the activated line is increasing. To t₃, many cells are activated and the cells around the activated line are distinctively more than before.

As assumed in assumption 3, the activation process is far from saturation, therefore, combined with the process description before, we can say that the more the cells have been activated at the point, the more the newly-activated cells may occur around this time. And we assume this relationship complies the following equation:

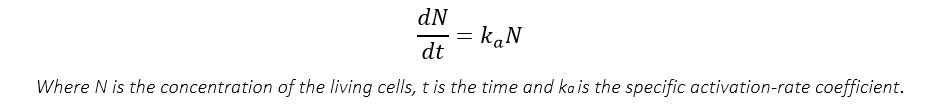
To make the following derivation easier, we divide both side of the equation by N₀, the initial number of yeasts.

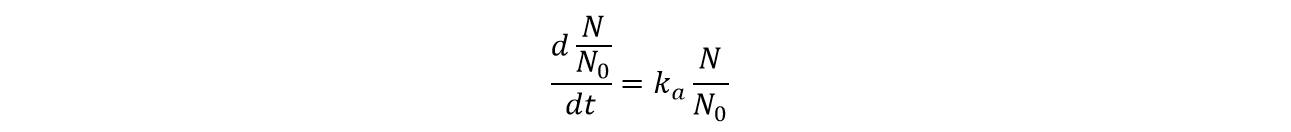
Then, after calculation and considering basic assumption 1, we get the formula of the amount of activated yeasts:

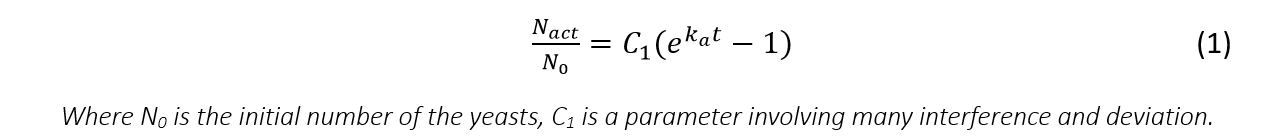
For proliferation part, we simply use exponential function with one parameter as:

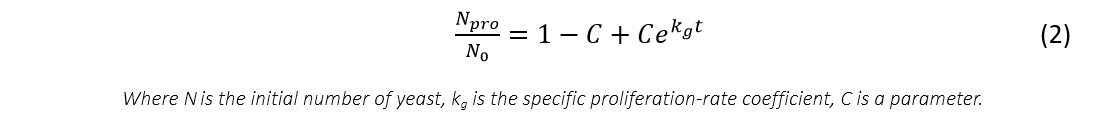
The total number of the cells at time t.

The cells at time t can be divided into three groups:

1. the proliferation cells originated from the activated cells, noted as N_act,pro
2. the inactivated cells, noted as N_inact
3. the dead cells, noted as N_dead

For N_act,pro

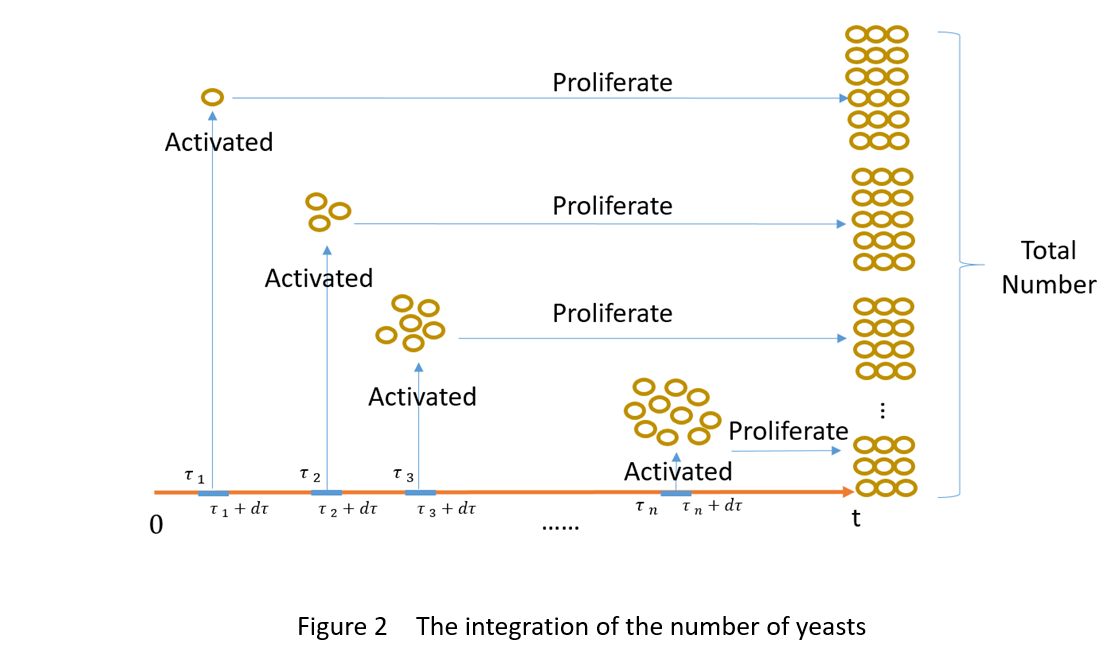
As is shown in figure 2, the total number of the proliferation cells at time t is the sum of the number of the proliferation cells originated from the cells activated in the time period of τ_n—τ_n+dτ (n=1,2…+∞).

And the number of the cells activated in the time period τ to τ+dτ can be derived from equation (1):

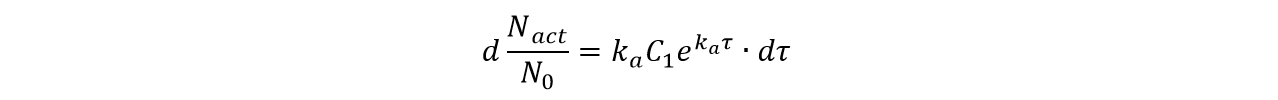
Then, considering the proliferation part of cell activated in the time period τ to τ+dτ, we can get the total number of the proliferation cells originated from the activated cells and the activated cells themselves by integration as follow:

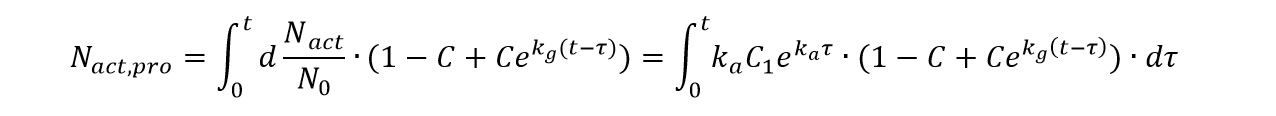
For Ninact and Ndead

We can get that:

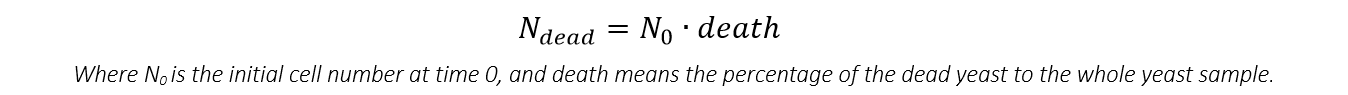
And

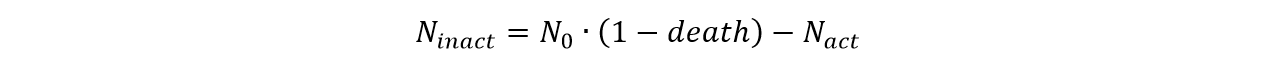
With Part_1,2,3,we can get the total number of the cells at time t as:

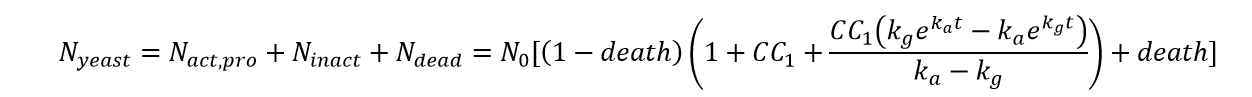
From the equation above can we know that what really contribute to the change of the number of yeasts is the multiplication of C and C₁ , not two single parameters. Considering assumption 3, we know that parameter C₁ is restricted to a small value, which at least follow the inequation:

Simulation and Results

Simulation

Numerical simulation

Firstly, we use the Levenberg-Marguard nonlinear optimization algorithm[1] to estimate the unknown parameter C, C₁, k_g and k_a and to forecast the dead yeast percentage , of which the criteria value is defined as:

Where i means the experimental data, the subscript exp represents the experimental data and sim denotes the simulated values from the model equations. We use C++ to build our algorithm. At first, we get initial value of these parameters that can simulate yeast number similar to the experimental data. Then we change these parameters a little(bigger, smaller or just stay), calculate f for every circumstance and choose the change corresponding to the smallest f as the new parameters. We repeat this step until f is minimized and the value of parameters are finally obtained.

For C and C₁, we try some pairs of values under the restriction of C₁ and find the pair with the smallest f.

Computer simulation

Then, we write a program to simulate the full process precisely. We consider every second as a time point and use the Monte Carlo method to simulate a random circumstance. And then we take the percentage of yeasts activated at that certain time point into account and judge if a yeast cell will be activated or not. We just use the parameters calculated in numerical simulation.

Results

The two figures and the two tables that list the value in the figure show activation process of two of our experiment groups. OD value[2] represent the size of the number of yeasts. We can see from these two figures that the two simulation curves are almost same as the real situation, which means that our model fit the real situation well.

The table shows that f of these two groups are both less than 0.03, and the dead cell percentage are both around 15%, which also means that our model fit the real situation well.

Reference

[1] Hui Huang , Marianne Su-Ling Brooks , Hua-Jiang Huang & Xiao Dong Chen (2009) Inactivation Kinetics of Yeast Cells during Infrared Drying, Drying Technology, 27:10, 1060-1068, DOI: 10.1080/07373930903218453

[2] Guozhen Cao, Jianshun Miu, Miaomiao Zhang, et. Determination of Saccharomyces cerevisiae cell suspension concentration by spectrophotometry[J], China Brewing, 2014, 33(4): 129-133.